
How many melodies are there?
The equivalent of a writer staring at a blank page, wondering how to fill it, is a composer staring at the 88 black and white notes on a piano wondering how to compose a melody that's never been heard before. How can one possibly take the eight notes of a standard scale and write a brand new melody when so many great melodies have already been written? Perhaps they've all been taken!

How many combinations are there?
So, to counter the fear of there being no new melodies, I thought it would be interesting to examine the number of melodies available to a composer looking at his blank stave to see how many there potentially are.
The first thing to do is to lay down some ground rules. These are:
- The melodies will be a single stream of notes — no chords, counter-melodies or basslines — just a single line of music. Remember the "old grey whistle test"? If it can be played on a tin whistle — it's a melody.
- For the first section I've discounted rhythm so as to focus only on the permutations of notes.
- All melodies should be contained within an octave — C to C' inclusive.
- Any of the 13 chromatic notes of the octave can be used. I've not restricted this to just a major or minor scale as many great melodies use accidentals (the black notes in a C major scale). So we can include all of the notes within the octave, including the octave jump (from C to C') as otherwise Over the Rainbow would not count as a melody! The notes are: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C'.
We will tackle this problem by starting with the simplest possible melody — one consisting of two notes — and then building up the melody length one note at a time until we see a pattern that can be turned into a formula.
Two note melodies
How many two note melodies can be written within an octave? This one is easy and all combinations can be written out:
| First note | Second note | Pitch difference (semitones) |
| C | C | 0 |
| C | C# | 1 |
| C | D | 2 |
| C | D# | 3 |
| C | E | 4 |
| C | F | 5 |
| C | F# | 6 |
| C | G | 7 |
| C | G# | 8 |
| C | A | 9 |
| C | A# | 10 |
| C | B | 11 |
| C | C' | 12 |
| First note | Second note | Pitch difference (semitones) |
| C' | C' | 0 |
| C' | B | -1 |
| C' | A# | -2 |
| C' | A | -3 |
| C' | G# | -4 |
| C' | G | -5 |
| C' | F# | -6 |
| C' | F | -7 |
| C' | E | -8 |
| C' | D# | -9 |
| C' | D | -10 |
| C' | C# | -11 |
| C' | C | -12 |
Now, you might be wondering why combinations like G# - F and E – A are not included. This is because we are only interested in relative pitch, not absolute notes. For the purposes of this exercise the melody C – C is identical to D – D or G – G as they are all unison melodies (i.e., they have 0 as their pitch difference). That's why we won't count the unison melody C' – C' — unison was already covered in the first table by C – C.
Having excluded C' - C' we have a total of 25 exciting two-note melodies!
Three note melodies
The number of three note melodies rises quite sharply, but not so much that they can't also be written out.
A small extract of the spreadsheet that lists all 2197 three-note combinations with duplicates in grey. You can see the whole spreadsheet here.
We can start by listing all possible combinations of three notes and then crossing out those that are duplicates. It turns out that it's easy to find duplicates: they are exactly those sequences of notes that don't have any C in them. Any melody without a C can always be moved down the scale until its lowest note becomes a C. Therefore, any melody without a C is a duplicate of a melody that does contain a C. To count all melodies, all we have to do is to count all sequences of notes than contain a C.
There are exactly 2,197 three-note combinations, out of which 1,728 don't contain a C. So there is a total of 2,197 – 1,728 = 469 three note melodies.
Not bad!
Four to infinity
Now, writing down all possible combinations of notes and picking out the ones with a C is not a very efficient way of exploring further, so we need an equation that will describe the increase in melodies. Suppose we are counting melodies made out of $n$ notes (so we've already covered $n=2$ and $n=3$). There are 13 choices for what the first note could be (one of C through to C'), 13 choices for the second note, and so on. This means that the number of all sequences of $n$ notes is $$\underbrace{13 \times 13 \times ... \times 13}_{n} = 13^n.$$ From this we need to subtract the sequences that don't have a C in them. For such a sequence there are 12 choices for the first note, 12 choices for the second note, and so on. So the number of all sequences of $n$ notes that don't contain a C is $$\underbrace{12 \times 12 \times ... \times 12}_n = 12^n.$$ Which tells us that the number of sequences of $n$ notes that do contain a C (the number of melodies) is $$13^n - 12^n.$$ We can even be more general and find the number of melodies for any scale. If the number of notes in the scale is $s$ (so in our case $s=13$) then the number of melodies that contain $n$ notes is $$s^n - (s-1)^n.$$ But let's return to our example with $s=13.$ Substituting ever larger numbers for $n$ — the length of the melody — gives us the following answer to our original question, the number of potential melodies within an octave:| Length of melody | No of possible melodies |
| 2 | 25 |
| 3 | 469 |
| 4 | 7,825 |
| 5 | 122,461 |
| 6 | ca. 1.84 million |
| 7 | ca. 26.9 million |
| 8 | ca. 385 million |
| 9 | ca. 5.4 billion |
| 10 | ca. 75 billion |
So, a mere ten note melody will produce over 75 billion potential melodies of 13 notes within the octave! It's going to take our composer a while to work his way through those. A computer would find it easier — if anyone out there produces a program that cycles through all of them, then please let us know!
Bring on the rhythm
It would be nice to factor in rhythm as well, just to be completist, as very few melodies are sequences of exactly the same length of notes.
Luckily this is much easier to compute. Potentially note lengths can be anything between a semiquaver (a sixteenth note) and a semibreve (a whole note). (I'm discounting hemi-demi-semiquavers!) Rather than include every single variation I think these would be a sensible selection of notes that would be available to use:
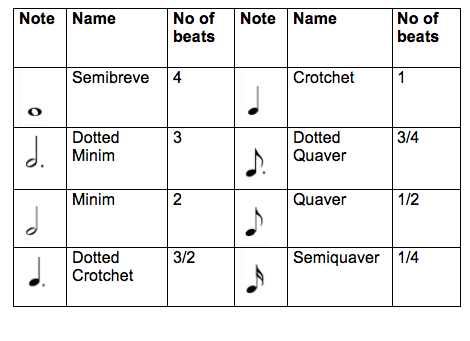
| Length of melody | No of possible note combinations | Rhythm variations (ignoring melodies) = 8n | Number of melodies (note combinations multiplied by rhythm variations |
| 2 | 25 | 64 | 1600 |
| 3 | 469 | 512 | 240,128 |
| 4 | 7,825 | 4,096 | 32 million |
| 5 | 122,461 | 32,768 | 4 billion |
| 6 | ca. 1.84 million | 262,144 | 4.8 x 1011 |
| 7 | ca. 26.9 million | ca. 2.1 million | ca. 5.6 x 1013 |
| 8 | ca. 385 million | ca. 16.8 million | ca. 6.4 x 1015 |
| 9 | ca. 5.4 billion | ca 1.3 x 108 | ca. 7.02 x 1017 |
| 10 | ca. 75 billion | ca. 1.1 x 109 | ca. 8.25 x 1019 |
Or, for that final number:
There are around 82,500,000,000,000,000,000 melodies that are 10 notes long.
That's a fair few to work through! A very rough approximation shows it's over 2.6 trillion years worth of material. And as mentioned at the start, this doesn't even begin to take into account the variations provided for by harmonisation, orchestration, tempo, or heavens above — bringing in a new counter melody!
So I think the message is: there is no excuse for writers' block.
About the author

Oli Freke is a London based musician and composer who's variously supported the Human League with electro band Cassette Electrik, written for TV and recently had club chart success with track Line-1. He is currently looking forward to working through all 8.25 x 1019 melodies in due course.
Comments
Anonymous
The number is surely not so large. Just as you have rightly equated a series of pitch differences starting on C with the same series starting on any other note, you should equate a series of pitch differences comprising only semibreves as being the same as the those pitch differences comprising only crochets. And is a 2 note melody, say C semibreve C minim, different to C minim C crochet, or C quaver C semiquaver, or even C demi-semiquaver C hemi-demi-semiquaver.
Perhaps we will run out of melodies after all
Anonymous
https://www.youtube.com/watch?v=GLyLxvFxHbU
Anonymous
If we are to do this we then would need to consider not the number of different values a note could have, but the ratio of counts between two notes (ex. two counts to four counts, which simplifies to one count to two counts). By making a list of all possible rations and simplifying them, you can see the repeats and cross those out as possibilities. You are thusly left with twenty four unique ratios. Because these are ratios between two notes, we must raise twenty four (the number of unique ratios) to the n-1 then multiply. This leaves us with the following values
2 notes: 600 melodies
3 notes: 270,144
4 notes: 1.08e8
5 notes: 4.06e10
As you can see, it quickly escalates into much larger numbers of possible melodies than when we only considered the values of separate notes. It does, however, give us a much more accurate set of values for the possible numbers of melodies. One may intuitively think this cannot be correct on the basis of note values. For example, take a note with a value of one count to a note of a value of two counts, a one to two ratio (my apologies for not including the correct note names; I do not know the British convention for note values) then for the third note, a three to two ratio to the second note. Although this may seem unappealing at first, it is possible because these are absolute, unique ratios, i.e. simplified. therefore as long as the third note is twice as long as one third of the second note, it is allowed. In this case, the note has a value of that note is four thirds, one of the established notes that is being used.
Anonymous
I talk about this in my maths teaching blog: see the "How Many Tunes" post at www.thewessens.net/blog
I used a very restricted musical space - just 2 bars, 12 notes (white notes from A below middle C to E an octave above), some constraints for musicality and restrictions on rhythm, and wrote a web app to explore (and listen to) the possibilities. It is at my website "The Mathenæum" at www.thewessens.net/maths and is called "Computer Composer". The blog post links to it as well.
It's a lot of fun, and quite incredible how many tunes are possible. Here's the conclusion from the blog:
Adding these together, we have a total of 22 059 rhythms (from 3 notes to 16 notes), leading to more than 50 000 000 000 000 000 tunes (that’s 16 zeroes — 50 quadrillion!). Including harmonies, we end up with a final number of 2 300 000 000 000 000 000 songs (2.3 quintillion). And remember, these are not just random arrangements, but we have used rules to greatly increase the chance of a resulting tune sounding musical (matching harmony, starting on C etc).
That’s a lot of tunes! A very lot. So many that it’s actually quite difficult to imagine, but this might help.
- If we were to only keep one in every million songs (assuming the others are too similar or not musically interesting) we would still have more than 2 trillion songs in total.
- If we started composing in this way the very instant the universe began, writing one song every second right up until now, we would still be less than 20% through all the possibilities!
- If we printed out all the songs in a line, each song taking up 15cm, the length of paper would go from Earth to Proxima Centauri (the nearest star after the Sun — about 4.23 light years away) and back more than 4 times. That’s about 36 light years.
Ken
Jim
The writer of the article is correct. People choosing to borrow ideas from others is sometimes about immediate influence from current styles and tastes, subconscious imitation, habits, ruts... Surely we could have more tire tread patterns on automobiles. But law inforcement needs to keep a manageable data base.
If you look at the possibilities on a lottery drawing and then compare that to the possibilities out there... There are even more than was suggested in this article as I don’t think he was suggesting that he had exhausted every possibility which would include non Western musical scales, etc.
Repeats are a result of human memory- intentional and unintentional.
M
I understand your view but, you have to take into account the notes it is being played with, I.e harmony. So with harmonic harmony in mind not just melodic harmony this initial concept is correct.
Rick Clayton
From a practical standpoint, you are correct - there should be more eliminations for "equal" rhythms, etc; not to mention questions of practicality, aesthetics, etc.
On the other hand, melodies can have much more than 10 notes, and each additional note increases the possible number of melodies exponentially - literally!
A somewhat similar example, which I also find mind-boggling: a normal human being is capable of producing over 8.3 million genetically unique offspring (ie, we have 23 pairs of chromosomes, and each egg/sperm cell gets 1 chromosome from each pair *at random*; so 23 pairs/sets, 2 possibilities from each one)
This gives us 2^23, which = 8,388,608.
This mean that with ONE man/woman couple, there are more than 70.3 TRILLION different possibilities for each of their offsprings' genetic makeup. (8,388,608^2 = 70,368,744,177,664). Of course we don't produce nearly this many children, females don't even produce close to 8.3 million egg cells. But per individual and couple, those numbers ARE what's *possible*.
Anonymous
There has not been a new melody since "Girls Just Wanna Fun" in 1983. What is scary is that nobody seems to notice.
Anonymous
I noticed :)
David S
Cyndi's 1983 version was a cover, it was first recorded in 1979 by American musician Robert Hazard.
Anonymous
It's something I have long thought, but about pictures: Since there is a finite number of pixels on any photo (or image) and the number of colors -perceptible or used- is also finite, it is concluded that the number of pictures or images possible is also finite, but very, very, very large. And a movie is just a sequence of a finite number of photographs, that is, the number of possible films is also finite.
Luis Guillermo Restrepo Rivas
Marcin Olak
This number is somewhere between Googol (10^100) and Googolplex (10^(10^100)). Or more precisely between 10^(10^22) and 10^(10^23).
The number of all colors modern graphic cards can represent is: 256^3 = 16.7M
The number of pixels in a full HD image is 1920 × 1080 = 2M
Now to get to the number all full HD we have to put (256^3) to the power of 1920 × 1080.
(256^3)^(1,920*1,080) = 1.5... × 10^14,981,179 = 10^(10^7.17...)
Let's call this number HD.
As a comparison Googol, a very very large number, is equal to 10^100. So HD is much greater than Googol but smaller than Googolplex (10^(10^100)).
Now onto movies. Let's assume they are silent movies, with no audio. Let's assume they last 90 minutes and are are filmed in 48fps.
So we get 90 * 60 * 48 = 259,200 frames.
Since every one of the 259,200 frames can be any of the HD images the number of all HD movies is
(10^(10^7.17...))^(0.26 * 10^5) ~= 10^(3.83 * 10^12)
Now for every conceivable soundtrack. Sampled at 44.1kHz and with 16bit resolution per each of the stereo channel has 90 × 60 × 44100 samples so there's (2^32)^(90 * 60 * 44100) different soundtracks i.e. around:
~10^(10^9.36).
In total you can have roughly 10^(10^22) different movies.
Lewis
Not too sure it that is completely correct. I'm no mathematician, (and don't it show) but i believe the figure to be much MUCH larger... Should the first (and in fact all) calculation be factorial (256^3)^(1,920*1,080)! Note the "!". Even my Word on my laptop can show in excess of 25000 digits on a single screen (which is a massive number in one frame), and we haven't even started on pictures, numbers or letters... or using the complete screen...! A googol of different screens would be simply 99 digits on the screen counting through. And that doesn't include the 16M different colors each of the pixels in each of the numbers could be...each of them factorial... Arrrrgh, it make my brain boil!
Anonymous
I think the use of "melody" is a slight misnomer - the article is really just talking about the potential number of different "SEQUENCES" of notes. The actual number of sequences which would result in anything that could be termed a "melody", rather than just a random cacophonous sequence, must be substantially less!
As to whether "Girls Just Wanna have Fun" counts as the former (a melody) or the latter (a cacophonous sequence) - well, that's a minefield I have no intention of entering!
Hang on, yes it is - it's the latter...
:-)
Anonymous
This is a good point, not to mention, not every combination or sequence will have a pleasing melody.
Zarlino
Thank you for doing the math, Oli. People(mostly musician/composers suffering from chronic depression) drag out the old line about "there are only twelve notes. All the melodies have been written already" a lot, and this gives me a comprehensive answer that I can email or text.
It's a big help, because I tend to sit the offender in a chair while I play out all the two, three , and four note possibilities I can think of. They usually run screaming from the room at some point, and I collapse from nervous exhaustion. A bad business, all around, really, and this saves all that.
Excellent work!
bert
'Melody, a sequence of single notes that is musically satisfying', a sequence of possibilities is rarely, to put it mildly, deserving of being called a melody.
Jared
I agree that there are nearly endless melody combinations. There are many factors. Is anyone considering the fact that notes can be repeated ,strung together in a melody? And broken down even further than 64th notes all which would change a Melody.
clifford b fisch
With all of these staggering possibilities, why do so many popular songs sound so similar? Especially when it comes to country music.
Surely the number of appealing melodies is far less than the number of unappealing melodies. Would anyone listen to a ten note melody utilizing just 2 notes?
Someone needs to write a program that looks at a music channel containing a million songs to empirically determine the number of unique appealing melodies and the number of repetitious appealing melodies. Then, by exclusion take the universe of unused melodies and see if any of them would be appealing. Since there are vast cultural differences in what constitutes an appealing melody, there must be a genetic component that determines who our brains process sound to sooth the savage beast. Has anyone used this data to assist jurists in deciding copy write infringement suits?
marshal
We should definerly include rhythm. But remove ones with similar ratios. So we get just the melody and that's it. You can always speed up or slow down. Then consider the different enumerations.of these melodies. So now a melody can have an enumeration or label like c23b58 and c23b59 etc. Then we can analyze the structures and relations amongst these melodies. And one would hope, find categories and maybe determine a measure for goodness of the melody.
KW
Careful, fellows. When i hear large numbers of melodies possible, i think, wow, that's going to make for an incredible number of "earworms!" Appealing melodies? That brings in: there is no accounting for taste. Given, most people will like the same melodies; a few will enjoy other melodies. The musical edge probably explores that grey area in between. Dance to your own drummer, ladies and gents.
Simona
Because they deliberately sit there cloning what's gone before, for commercial gain. The top 40 has got nothing to do with art anymore.
Rick Clayton
So many popular songs sounding so similar? I'm sure one factor is that there are certain harmonic progressions (ie, 'chord changes') that tend to be aesthetically pleasing to large numbers of people, so they get used A LOT. This in turn greatly reduces the possible melodies (or 'sequences') to only ones that are compatible with these harmonic progressions.
A ten-note melody utilizing just two notes? Not exact, but close enough to make a point - in the main theme from "Jaws", significant sections, more than 10 notes in length, utilize only 3 notes. Yet in that context it worked very well, and was extremely successful...still well-known, after almost 50 years. A 'melody' (or sequence, motif, theme, etc) doesn't need to be purely aesthetic or 'pleasing/entertaining' to be useful.
Quentin
And they did: http://allthemusic.info
A lawyer who hated the music lawsuits over melodies got together with a programmer to write some code to generate all possible 8 and 12 note melodies and to copyright them, and put those copyrights into public domain to prevent people from claiming ownership over such melodies.
Walter Tau
For a person with normal (not absolute pitch) hearing ( and for the purpose of the Copyright Law), the key of the melody is immaterial. This immediately reduces your estimate by a factor of 12. Furthermore, most (>99% ?) series of random pitch jumps would not be considered a melody but a cacophony. I suspect the actually number of possible "ear-pleasing" melodies is within reach of one generation of 5 bln. people. Soon , we will be hearing mostly recycled music. And it's OK, since copyrights do not last forever.
Bullshit
I've written over 300 songs and all of them are ''ear pleasing''. The real number is limitless. There's a never-ending well of inspiration out there and it is made up of more than 6 notes. It's those notes, the chord, the key changes (very important, but top 40 doesn't know how to do it), Rhythm, Harmony, arrangement, production, etc. which all do wonderful things to camouflage what's been before and make it sound like it's being heard for the first time.
Ishmaeli
I think the fourth ground rule is a bit of a stretch. The fact that many melodies do include accidentals should not be taken as license to eschew key altogether, if the aim is to wind up with anything we could call a "melody."
This makes about as much sense as trying to count the number of possible words by computing possible combinations of letters. Most of the results will be gibberish.
foo
Considering that a dictionary contains thousands words, how many different 10-word comments can we write?
There's no reason for writers block!!!
So, here's my comment about this post:
"Huttonian fingering diacoustics tigh monomaniacal flinger chesses carbostyril invest toothbrush"
'Nuff said.
Waimea
This is hilarious. well said.
Tatarize
Yeah, some people have cycled through them all and committed the midis to disk. It means they own all the copyrights on all possible melodies unless they were committed to a medium earlier than they did.
They gave a TED talk on the process.
Anonymous
They also released them on public domain so big music industries cannot prey on small artists looking to make new music. Also, while the number of possible note sequence/melody is big, there's only so many sequence of notes that will actually sound pleasing.