
The economic analogy
This article is part of the Finance and physics package. Click here to see the previous article in the series.
So let's get on to the economic model. We imagine we have a collection of countries. Each country has its own currency. Let us imagine that the countries are arranged on a regular grid on a flat world. See the figure below. Each country is connected with its neighbours by a bridge. At the bridge there is a bank. There you are required to change the money you are carrying into the new currency, the currency of the country you are crossing into.
There is an independent bank at each bridge. There is no central authority coordinating all the exchange rates between the various countries. Each bank is autonomous and sets the exchange rate in an arbitrary way. The bank charges no commission.
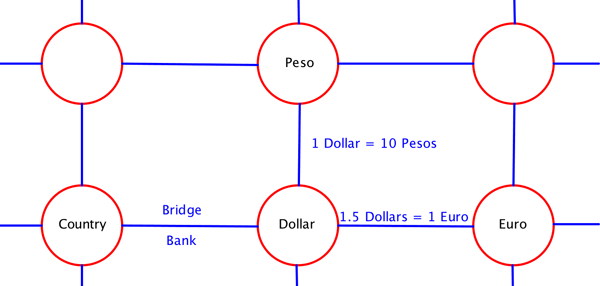
Each circle is a country that has its own currency. They are connected by blue bridges. At these bridges there is a bank. When you cross the bridge, you should change all your money to the new currency. We have indicated some of the currencies and exchange rates. At each bridge there is an independent exchange rate.
For example, assume that the currency in your original country is Dollars and the one in the new country is Euros. Suppose that the exchange rate posted by the bank at the bridge between two countries is 1.5 Dollar = 1 Euro. Then if you have 15 Dollars the bank converts it to 10 Euros as you cross the border. If you decide to come back your 10 Euros will be converted to 15 Dollars. Therefore, if you go to a neighbouring country and you come right back, you end up with your original amount of money.
Another rule is that you can only go from one country to the neighbouring country. From there you can continue to any of its neighbuors and so on. However, you cannot fly from one country to a distant country without passing through the intermediate ones. You can only walk from one to the next, crossing the various bridges and changing your money to the various currencies of the intermediate countries.
The final assumption is that the only thing you can carry from one country to the next is money. You cannot carry gold, silver, or any other good. We will later relax this assumption, but for now we will consider this simplest situation.Knocking off zeroes
So where is the gauge symmetry? Imagine that one of the countries has accumulated too many zeroes in its currency and wants to drop them. This is fairly common in the real world in countries with high inflation. For example, instead of using Pesos now everybody needs to use Australes. The government declares 1,000 Pesos will now be worth 1 Austral. So everybody changes all prices and exchange rates accordingly. If you needed to pay 5,000 Pesos for a banana, now you will need to pay 5 Australes. If your salary was 1 million Pesos, it will now be 1 thousand Australes.
Suppose the neighbouring country is the USA. If the exchange rate was 3,000 Pesos = 1 Dollar, Dollar, it will now be 3 Australes = 1 Dollar. We call this a gauge symmetry because after this change nothing really changes, nobody is richer or poorer and the change offers no new economic opportunities. It is done purely for convenience. And it does not change anything physical, like the number of bananas you can buy with your salary. The word "gauge", meaning measuring device, highlights that this is only a change in the units we use for measuring, but not a "real" measure of anything.
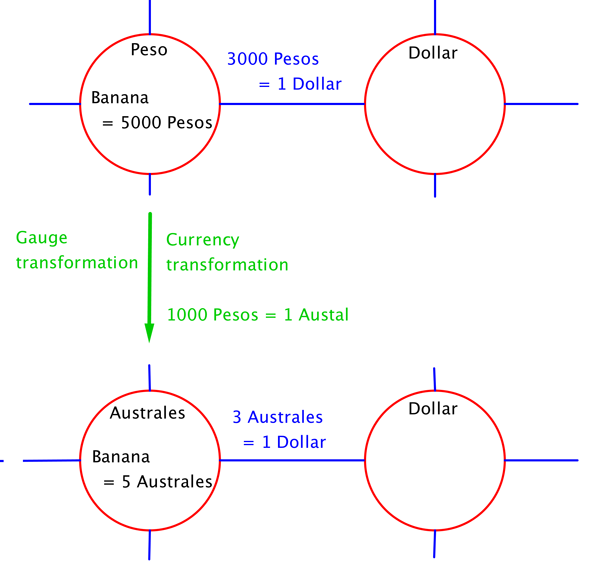
Each country can change its currency units. Here the country that was using Pesos changes the currency to Australes so that 1000 Pesos = 1 Austral. All prices and exchange rates change accordingly. Here we indicated how the price of a banana would change. We have also indicated how the exchange rate to one of the neighbouring countries changes. Of course, the exchange rates with all the neighbours change.
You can see this gauge symmetry in action in some Argentinean banknotes.

A gauge symmetry in action. Here we see a real world change from Pesos Argentinos to Australes.
The gauge symmetry is local in the sense that each country can locally decide to perform this change, independently of what the neighbouring countries decide to do. Some countries might like to do it more frequently than others. In the real world Argentina has eliminated thirteen zeros through various actions of this "gauge symmetry" since the 1960s, so that 1 Peso of today = 10,000,000,000,000 Pesos of the 1960s.
How to make money in a simple world
Now we will focus on speculators. A speculator is somebody who will travel along various routes converting money as he or she crosses each bridge. The goal is to earn money. The speculator wants to travel along the paths with the highest monetary gain. Recall that according to our rules he or she has to actually travel to the different countries. You can't just sit at a desk and order trades on a computer.
Do you think you can make money in this world? Think about it, what would you look for?
At first sight it seems that you cannot make any money. In fact, if you go from one country to its neighbour and back, you end up with the same amount of money. However, it is possible to make money if you come back a different way!
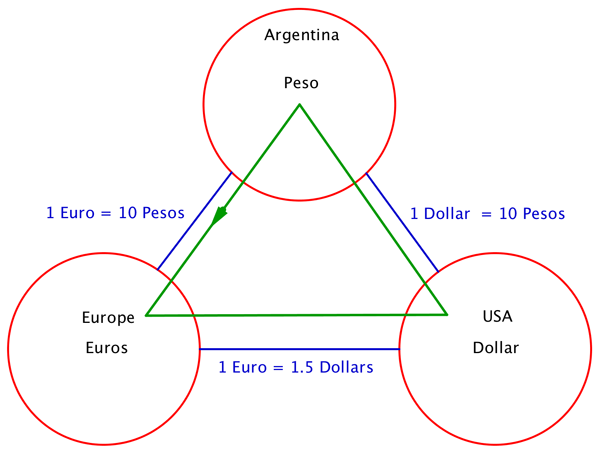
Here we see three countries with the respective currencies. On the blue bridges we see the corresponding exchange rates. If you follow the circuit along the green line, you would earn money. You would have a gain factor of 1.5 or earnings of 50%.
As an example let us consider three currency regions, say the USA, Europe and Argentina, with their corresponding currencies Dollars, Euros, and Pesos. Now let us imagine that there are bridges connecting these three countries, see the figure above.
The exchange rates are as follows:
1.5 Dollars = 1 Euro
1 Dollar = 10 Pesos
1 Euro = 10 Pesos
We can earn money by starting in Argentina with 10 Pesos, then going to Europe to get 1 Euro, and then going to the USA to get 1.5 Dollars. Finally we go back to Argentina and get 15 pesos. We started with 10 and ended with 15. The gain of this circuit is a factor of 1.5, or earnings of 50%. If you started the circuit with X Pesos, you would have 1.5 x X Pesos at the end. This factor is independent of the currency units. If the Argentinean government changes from Pesos to Australes, then the gain of the circuit is still the same, it is still a factor of 1.5.
You might think that the banks were dumb to set the "wrong" exchange rates and that speculators are taking advantage of them. Well, this is according to the rules we have enunciated. The banks set the exchange rates they want. With some choices there will be opportunities to speculate and with some others there will not be. The speculators have a very simple mind, they only care about earning money and they will choose the path that makes them earn most money. In the above situation the speculators would be moving in circles going from Argentina to Europe to the USA and back to Argentina. They would be following the green line in the figure above.
Previous article: A quick introduction to electromagnetism Next article: Electromagnetic economics
Back to the Finance and physics package
These articles contribute to our Stuff happens: The physics of events project.
About the author

Juan Maldacena is the Carl Feinberg professor at the Institute for Advanced Study at Princeton, New Jersey, USA. He works on quantum field theory and quantum gravity and has proposed a connection between those two (see this article).