
Leaning into 2012
Rising like a giant pringle from the Olympic Park construction site, the Velodrome is the first of the 2012 London Olympic venues to be completed.

The London Velodrome.
With its sweeping curved roof and beautiful cedar clad exterior the Velodrome is a stunning building. But what most of the athletes are excited about is the elegant wooden cycle track enclosed inside, the medals that will be won, and the records that might be broken, in the summer of 2012.
The track is a symmetrical circuit, 250m long, made up of two long straights linked by two 180 degree turns. And like all velodromes the track is sloped, from around 12 degrees on the relatively flat straights up to 42 degrees at the steepest part of the banked turns.
Seen from the centre or looking down into the turns from the spectator seats the banked turns seem perilously steep. But rather than tackling the slopes with caution cyclists use these steeply banked turns to create the high speeds necessary to fly around the track.
In order to move on a circular path you need an inward force, called the centripetal force, to pull you into the turn and stop you shooting off along a straight line. If you have a mass $m$, a speed $v$ and you are turning around a circle of radius $r$, then the centripetal force to move in this circular path at that speed is $$Centripetal \;\;\; force = \frac{mv^2}{r}.$$ The centripetal force can be a pulling force, like the force exerted when you swing a ball tied to the end of a string. But it can also be a pushing force, which comes from us instinctively leaning into a turn when riding a bike or running around a tight corner.

The London Velodrome's track is designed for maximum speed.
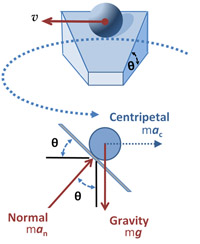
The forces acting in a banked turn. Image: Brews ohare.
"In effect, on every banking a rider climbs a small hill on entry to the banking and descends the hill as he leaves the banking and enters the straight," Dave Cockram, the National Facilities Officer for British Cycling, told Engineering and Technology Magazine. "The optimum design is one that allows a rider to travel at the maximum speed with the minimum effort and the design of tracks has evolved over the years from two long flat straights with two banked circular turns into very complex geometry involving short straights with slopes of 10 degrees or more, transition curves with steadily increasing banking angles leading into circular curves with banking angles of around 45 degrees and transitions back into the straights of different slopes and radii."
Suppose you had a banked turn with the track tilted at angle $\theta$ degrees to the horizontal and following a curve of radius $r$. Then if we ignore the effect of friction and the bike and rider remain perpendicular to the tilted track, the track pushes up with a force $F$ at an angle of $\theta$ to the vertical. So the vertical componet of this force, which is $F \cos{\theta},$ is exactly equal to the vertical force due to gravity, $mg,$ of the rider and bike: $$F\cos{\theta} = mg.$$ The horizontal component of this force, $F\sin{\theta},$ is exactly equal to the centripetal force, $mv^2 / r,$ where $v$ is the speed of the cyclist: $$F\sin{\theta} = m v^2 /r.$$ Bringing these two equations together then gives what's known as the {\em rated speed} of the curve: $$v = \sqrt {r g \tan{\theta}}.$$
This is the speed at which the cyclist can move through the turn due to the geometry alone, without any help from the force of friction. The rated speed of a turn banked at 42 degrees around a curve of radius 25m is around 54km/h. But the same curve on a flat track would have a rated speed of zero — the only way you could follow that curve is to lean into the turn and rely on the friction of the track, and leaning at an angle of 42 degrees while moving at 54km/h is a risky business.
The Velodrome track has been designed to produce world-record-beating times. But the geometry of speed has also inspired the curves of the sweeping roof and the cedar clad exterior. The external shape of the building allows for seating around the whole of the track, creating, according to Olympic cycling legend Chris Hoy, a "wall of noise" and a "gladiatorial atmosphere". Let the games begin.
Further reading
- There is an excellent explanation of circular motion in athletics, including speed skating and cycling on physicsclassroom.
- You can go on a virtual tour of the new velodrome.
- Here's a nice article on the velodrome in The engineer.
- And you can read about the centripetal force and banked turns on Wikipedia.