The lines of intersection and metallic numbers
We are looking at an infinite family of circles. The first circle is centred on the point $(0,0)$ and has radius $1$. Every other circle is centred on the South pole of the previous circle and has radius $A$ times that of the previous circle. (In the first example in the main article we have $A=\sqrt{2}$, but we give a sketch of the proof for general $A$.)
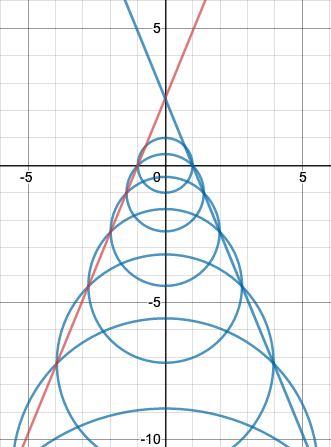 We want to show that all the intersection points that lie on the same side of the $y$-axis lie on a straight line, as shown in the diagram above.
We will also show that the two lines of intersection meet the $y$-axis in the point $(0,1/(A-1)).$ If $A=A_n=\lambda_n-(n-1)$ we have
$$\frac{1}{A-1}=\frac{1}{\lambda_n-n}=\lambda_n,$$
as claimed in the main article.
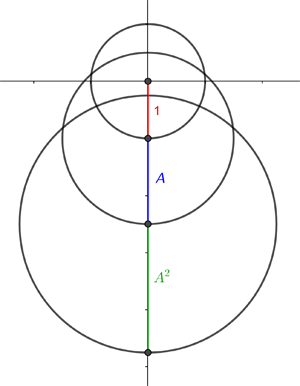
First notice that the radius of the $nth$ circle is $A^{n-1}$. This is because the first circle has radius $1$ and any other circle has radius $A$ times the radius of the previous circle.
Also notice that for $n\geq 2$ the $nth$ circle has centre $(0,-(1+A+A^2...+A^{n-2})).$ That's because the centre of the first circle is $(0,0)$ and the $y$-coordinate of the centre of any other circle is the $y$-coordinate of the centre of the previous circle minus the radius of the previous circle. (The first circle has centre $(0,0)$.)
We want to show that all the intersection points that lie on the same side of the $y$-axis lie on a straight line, as shown in the diagram above.
We will also show that the two lines of intersection meet the $y$-axis in the point $(0,1/(A-1)).$ If $A=A_n=\lambda_n-(n-1)$ we have
$$\frac{1}{A-1}=\frac{1}{\lambda_n-n}=\lambda_n,$$
as claimed in the main article.
First notice that the radius of the $nth$ circle is $A^{n-1}$. This is because the first circle has radius $1$ and any other circle has radius $A$ times the radius of the previous circle.
Also notice that for $n\geq 2$ the $nth$ circle has centre $(0,-(1+A+A^2...+A^{n-2})).$ That's because the centre of the first circle is $(0,0)$ and the $y$-coordinate of the centre of any other circle is the $y$-coordinate of the centre of the previous circle minus the radius of the previous circle. (The first circle has centre $(0,0)$.)
 Our proof rests on the fact that there is quite a simple transformation of the plane which sends each circle in the family to the next one along. This transformation, call it $f$, consists of a scaling by a factor of $A$, followed by a translation by 1 in the direction of the negative $y$-axis. In other words, $f$ sends a point with coordinates $(x,y)$ to the point with coordinates $(Ax,Ay-1).$
Our proof rests on the fact that there is quite a simple transformation of the plane which sends each circle in the family to the next one along. This transformation, call it $f$, consists of a scaling by a factor of $A$, followed by a translation by 1 in the direction of the negative $y$-axis. In other words, $f$ sends a point with coordinates $(x,y)$ to the point with coordinates $(Ax,Ay-1).$
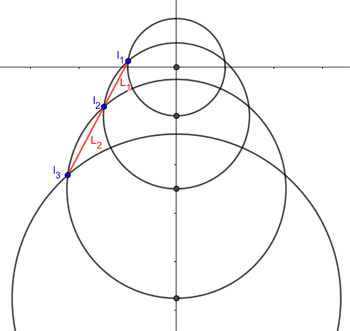 By point (2) above, $f$ sends $L_1$ to another straight line segment
(rather than some curvy shape). Because $f$ sends each circle to the next one along, that line segment, call it $L_2$ is the one connecting the intersection points $I_2$ and $I_3.$ Point (2) also says that $L_1$ and $L_2$ have the same slope — and from this it follows that $I_1$, $I_2$ and $I_3$ all lie on a straight line. You can apply the same argument to other line segments connecting consecutive intersection points, to show that all intersection points lie on the same straight line, call it $L$.
The argument above also shows that $f$ sends $L$ to itself. This implies that
$$Ab-1=b.$$
Rearranging gives
$$b=1/(A-1),$$
as required.
By point (2) above, $f$ sends $L_1$ to another straight line segment
(rather than some curvy shape). Because $f$ sends each circle to the next one along, that line segment, call it $L_2$ is the one connecting the intersection points $I_2$ and $I_3.$ Point (2) also says that $L_1$ and $L_2$ have the same slope — and from this it follows that $I_1$, $I_2$ and $I_3$ all lie on a straight line. You can apply the same argument to other line segments connecting consecutive intersection points, to show that all intersection points lie on the same straight line, call it $L$.
The argument above also shows that $f$ sends $L$ to itself. This implies that
$$Ab-1=b.$$
Rearranging gives
$$b=1/(A-1),$$
as required.

The family of circles with the two lines of intersection. The y-intercept is the silver ratio.

The centres and radii of the first three circles.
We leave the following two facts for you to prove:
- The transformation $f$ sends a circle with centre $(0,c)$ and radius $r$ to circle with centre $(0,Ac-1)$ and radius $Ar.$
- The transformation $f$ sends a straight line with equation $y=mx+b$ to the straight line with equation $y=mx+Ab-1$.

Points of intersection and the line segments connecting them.
Back to the main article.