The fingernail problem and metallic numbers
In this article we will look at a beautiful geometric problem and its link to a very special family of numbers: metallic numbers, which arise as generalisations of the famous golden ratio.
We looked at metallic numbers in a previous Plus article, but here's a quick recap. The golden ratio arises from the following geometric problem. Given a piece of line, divide it into two segments so that the ratio between the entire line and the longer of the two segments equals the ratio between the longer of the two segments and the shorter one.

We'd like (A+B)/A = A/B.

The silver ratio arises from dividing the initial line like this.
Now let's move on to our geometric problem with its intriguing link to metallic numbers. It starts off quite simply, with a question involving the trimming of fingernails.
The fingernail problem
Suppose you want to cut your fingernails but misplaced your only pair of nail clippers. You do, however, own a pair of straight scissors. Could you, with a series of straight cuts, form a smooth, round, shorter fingernail?
Let's analyse this problem by first making a few simplifying assumptions. We could, to begin with, approximate the shape of fingernail with a semi-circle. We will use a semi-circle of radius 1 for convenience:
A semi-circle of radius 1.
We also need a fairly straightforward procedure with which to cut the fingernail. For this, we begin by first cutting the circle into a triangle with two equal sides, like so:
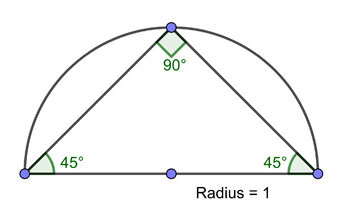
A semi-circle of radius 1.
We call the bottom line in this figure the base edge. Apart from the base edge, every other side (let's call these other sides exposed edges) has equal length. By Pythagoras' theorem the exposed edges have length $\sqrt{2}$. At every next step, a corner of the shape is clipped off so that the shape has one more exposed edge, and the new exposed edges all have the same length:
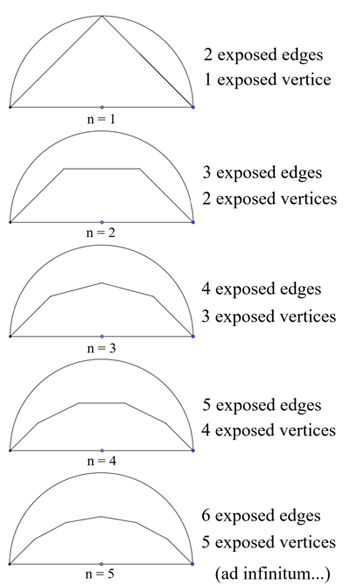
The cutting procedure.
Every successive cut produces a part of a regular polygon with more sides than the one before. If we had an infinite amount of time, we could continue the cutting procedure forever, and the number of sides of the polygon would tend to infinity. It turns out (as with similar problems with full circles, as shown below) that this will eventually produce an arc of a circle.
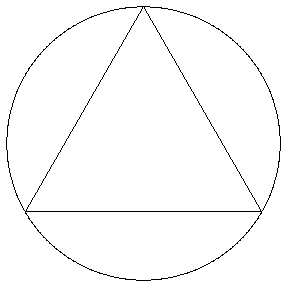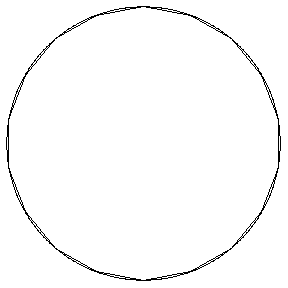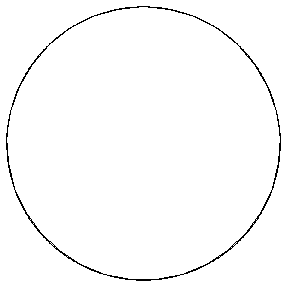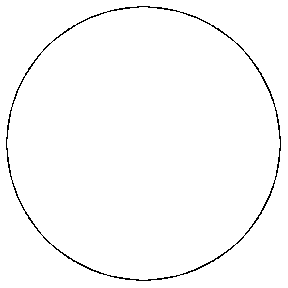
Adding sides to a regular polygon produces a circle in the limit.
Enter the silver ratio
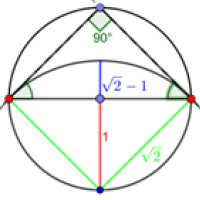
How much shorter is the newly cut fingernail compared to the original one? To work this out let's first find the defining features of the circle $O$ whose arc describes your newly cut fingernail. First note that the two end points of the base side of our triangle (shown in red in the diagram below) are points on the final circle. That's because in our procedure these points are never cut off. The two exposed sides of the equilateral triangle are tangent to the final circle.
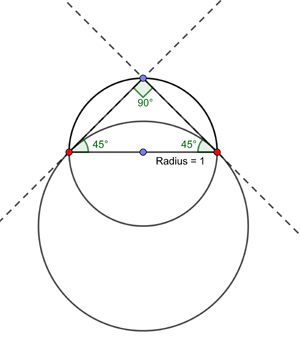
The end points of the base side are points on the circle O, and the two exposed sides of our triangles are tangent to the circle at these points.
A line that is tangent to a circle at a given point is perpendicular to the radius of the circle which ends at that point. Our construction therefore gives us two radii of $O$, shown in green in the diagram below.
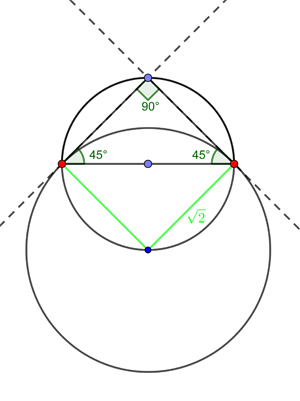
The green lines are radii of the circle O.
A little inspection of the symmetry in the diagram will convince you that the two radii have the same length as the exposed side of the original equilateral triangle, namely $\sqrt{2}$, and that the two radii meet exactly at the "South pole" of the original circle. The meeting point of two radii of the circle O is of course the centre of O. So we now know that O is centred on the South pole of the original circle and has radius $\sqrt{2}$.
Now let's use the base line of the original triangle as the line from which to measure height. The height above this base line of the original fingernail is 1 (the radius of the original circle).
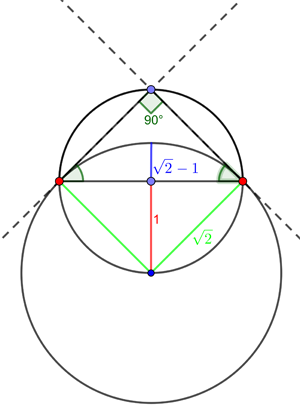
The ratio of the height of the old fingernail and the height of the new fingernail.
A family of circles
In our problem above we had two circles: the second circle is centred on the South pole of the first and has radius $\sqrt{2}$ times that of the first. We can now construct a third circle: as its centre we take the South pole of the second circle and for its radius we multiply the radius of the second circle by $\sqrt{2}$. In the same way we can construct a fourth circle from the third, a fifth from the fourth, and so on, giving us an infinite family of circles. In this family every successive circle has radius $\sqrt{2}$ times the ratio of the previous circle and is centred at the South pole of the previous circle.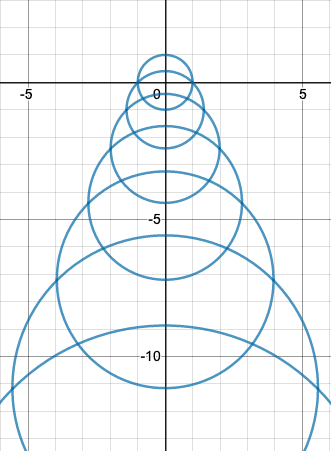
A family of circles.
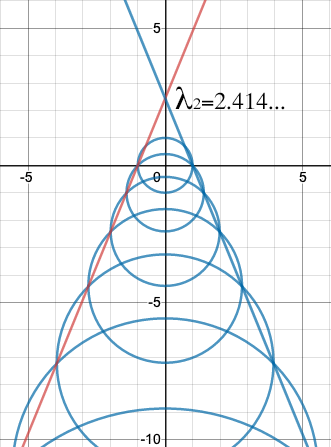
The lines of intersection associated to our family of circles. The y-intercept is the silver ratio.
It turns out that these two lines of intersection again involve the silver ratio: the point at which they meet the $y$-axis (and each other) has coordinates $(0,\lambda_2)$. (You can work this out for yourself or see the calculation here.)
It seems that the silver ratio is written all over our extension of the fingernail problem! And if you do the calculations, you will find that this seems to hinge on the fact that $$\frac{1}{\lambda_2-2}=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1 =\lambda_2.$$Other metallic numbers
This suggests that we may be able to generalise the construction of our family of circles to get all other metallic numbers too. One thing we could change is the ratio of the radii of successive circles. Let's call this ratio $A$. In the above construction we had $A=\sqrt{2}$, which is related to the silver ratio as follows:
$$A=\sqrt{2} = (\sqrt{2}+1)-1=\lambda_2-1.$$ So what if, for any other natural number $n$, we choose this ratio to be $A_n=\lambda_n-(n-1)$ by analogy? The first circle in our family will again be centred at $(0,0)$ and have radius $1$. The second will be centred at the South pole of the first, so that's the point $(0,-1)$ and have radius $A_n$. The ratio between the height of the top of the first circle above the $x$-axis and the height of the top of the second circle above the $x$-axis is $$\frac{1}{A-1}=\frac{1}{\lambda_n-n}=\lambda_n.$$ That's exactly analogous to the result we got above, where arcs of the two circles represented fingernails.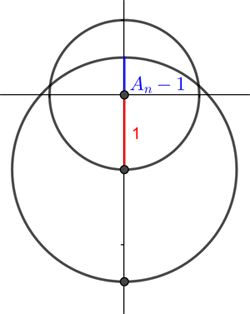
Ratio between the heights of the arcs of the circle above the x-axis.
What about those lines of intersection? It's possible to show (see here) that for $A=\lambda_n-(n-1)$ these meet the $y$-axis at (and each other) at the point $(0,\lambda_n)$.
The interactive below lets you play with different values for the ratio $A$. Move down the left panel to find the slider that varies $A$. To make the left panel disappear so you can see more of the graph, click on the double arrow at the top right of the panel. To help you find the values corresponding to the metallic numbers, the first four are:
\begin{eqnarray*}A_1&=&\lambda_1-0&=&\lambda_1 \approx 1.618\\ A_2&=&\lambda_2 -1 &=& \sqrt{2} \approx 1.414\\ A_3&=&\lambda_3 - 2 & \approx& 3.303 - 2 =1.303\\ A_4&=&\lambda_4 -3 &\approx &4.236 - 3 =1.236.\end{eqnarray*}Thus, a simple problem about a fingernail opens a door to an infinite collection of very special numbers!
About the authors
Gokul Rajiv is a first year computer science and mathematics student at the National University of Singapore and Yong Zheng Yew is a first year engineering student at the Singapore University of Technology and Design. They worked on the fingernail problem when they were at high-school and found it interesting enough to share.
