Article
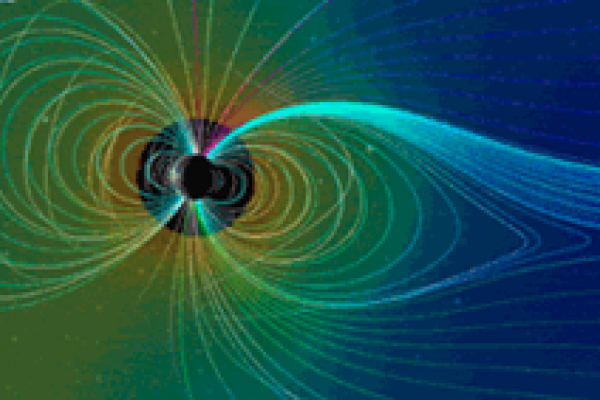

Why is the Earth a magnet?
It's a good question with a fascinating answer.



What do we know about mpox, what do we not know, and what efforts are going into modelling it?





Maryna Viazovska has won one of this year's Fields Medals for a ground-breaking result in the theory of sphere packings.


Barry Mazur has received the 2022 Chern Medal for profound discoveries in topology, arithmetic geometry and number theory.

