
The Abel Prize 2022: Dennis Sullivan

Dennis Sullivan. Photo: John Griffin/Stony Brook University/Abel prize.
This year's Abel prize has been awarded to the US mathematician Dennis Sullivan for ground-breaking work in a range of mathematical topics. The Abel prize is one of the highest accolades in mathematics. Awarded annually by the Norwegian Academy of Science and Letters, it honours the entire body of work of the mathematicians who receives it and comes with nearly £650,000 in prize money.
Sullivan has worked in a "dazzling variety" of mathematical areas. These include topology, which studies geometric shapes without paying attention to exact geometric quantities such as lengths, areas or angles (see here) and the study of dynamical systems. As is often the case with brilliant mathematicians, Sullivan's ability to draw connections between seemingly distinct areas has been a key to his success. According to the Abel prize citation, "Dennis Sullivan's insistent probing for fundamental understanding, and his capacity to see analogues between diverse areas of mathematics and build bridges between them, has forever changed the field."
Hopping along
In the area of topology, Sullivan made important contributions to an endeavour central to the field: understanding all the topological shapes that exist in a given dimension (see here for a brief introduction). But, having studied dynamical systems for my PhD, I was particularly excited about Sullivan's contributions in this area. As the name suggests, dynamical systems involve some sort of change that can be described by mathematical expressions.
As an example, take the equation $$y=x^2.$$ This doesn't appear particularly dynamical, until you realise that you can apply it again and again. For example, imagine you are sitting on the number line at the point $x=2$ and have decided that you are going to jump to the number you get when you plug $x=2$ in the equation. That number is $$y=2^2=4,$$ so you hop two units along. If you now apply the equation again to this result, you get $$y=4^2=16,$$ prompting you to hop ahead to $16.$ Applying it again to the latest result gives $$y=16^2=256,$$ causing you to take quite a leap. Doing this indefinitely (this is called iteration) you find that your motion along the number line is given by the sequence $$2,4,16,256,65536,4294967296...,$$ which is called the orbit of the initial value $x=2.$
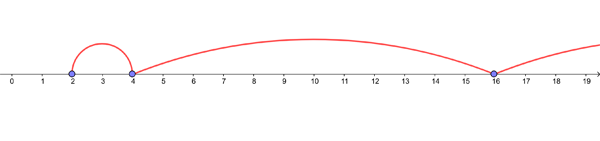
Hopping along the number line.
The orbit you get can depend very much on the initial value you choose. For $x=2$ your journey takes you rapidly towards infinity, but for the initial value $x=1/2$ it takes you towards 0 in ever decreasing steps: $$1/2, 1/4, 1/16, 1/256, .....$$ And if you started at $x=0$ you'd get stuck where you are, since $$0^2=0.$$
Chaos and fractals
Rational maps
A rational map is of the form $$R(x)=\frac{P(x)}{Q(x)},$$ where $ P(x)$ and $Q(x)$ are polynomials. Polynomials have the form $$P(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0,$$ where the coefficients $a_i$ are constants.
A rational map is not defined for values of $x$ at which $Q(x)=0$, so it is not defined everywhere on the complex plane. However, there is a way around this by defining the rational map on the Riemann sphere, rather than the complex plane. Find out more here.
The dynamics in the example above was confined to the number line, but there is a way (using complex numbers) to make equations like the one above direct the motion of points on the two-dimensional plane. You start at any point on the plane you want, and the equation tells you where to hop next, with iteration taking you on a never-ending journey around the plane.
The dynamics that arise were studied in the early twentieth century for a family of equations known as rational maps, of which our example above is a member. But it was only when computers made it possible to calculate long parts of an initial value's orbit, and to plot these orbits, that mind-blowingly beautiful pictures like the following were revealed.

The Julia set associated to the function y=x2-1. The Julia set is indicated in white. The remaining part of the image (the green and blue areas) belongs to the Fatou set. As you can see, the Fatou set consists of many individual components in this case.
(See the box above to find out what rational maps are—strictly speaking, they are defined on the Riemann sphere rather than the plane.)
The picture above shows the Julia set associated to the equation $y=x^2-1$ (when applied to complex numbers). Julia sets are named after the mathematician Gaston Julia, and they represent a kind of watershed of the dynamics dictated by the equation: points on the Julia set behave very differently from those around them. Orbits that start on the Julia set always stay on the Julia set and the dynamics there is chaotic in the mathematical sense: even if two initial values are incredibly close to each other, their orbits don't stay that close together. Julia sets of rational maps are usually fractals of breathtaking intricacy.
The rest of the plane, consisting of all the points that are not in the Julia set, is called the Fatou set, after the mathematician, Pierre Fatou. Orbits that start in the Fatou set always stay on the Fatou set, but this time the dynamics is more orderly. Loosely speaking, orbits that start close together stay close together. Technically speaking, the dynamics is equicontinuous on the Fatou set. (There are many more things we could say about Julia and Fatou sets, find out a little more on the topic in Unveiling the Mandelbrot set.)

Another Julia set, shown in green, this time for the function y = x2+c where c is approximately equal to the complex number -0.51+i0.52. The blue area belongs to the Fatou set. In this case the Fatou set consists of just one component. Image: Morn, CC BY-SA 4.0.
No wandering components
Once the beautiful structures associated to rational maps were discovered, a multitude of questions posed themselves. As you can see in the plots above, the Fatou set consists of components that are separated from each other by bits of the Julia set. And although you might not be able to see it because the components get too small, there can be infinitely many of them. This is the case for first plot above. For the second, the Fatou set only consists of one component, shown in blue.
If you apply the corresponding equation to an entire component, you will find that it is moved neatly onto another component (which might be itself). One question that arose naturally when people first studied the dynamics of rational maps was whether there could be a component whose orbit visits infinitely many other components, without ever becoming periodic. Such a component would be called a wandering domain.
This was an easy question to ask that turned out to be incredibly hard to answer. But in 1985, when the question was over 60 years old, Sullivan found a solution, to huge acclaim. His no wondering domains theorem showed that the orbits of all components of the Fatou set of a rational map eventually become periodic, moving through the same cycle of components again and again.
Making connections
To prove the no wandering domains theorem Sullivan made a brilliant connection with a result from a class of dynamical systems that at first sight appear very different from the ones you get from rational maps. A Möbius transformaton is an expression of the form
$$y=\frac{ax+b}{bx+c},$$ where $a$, $b$, $c$ and $d$ can be real or complex numbers. Two examples are $$y=\frac{x+1}{x-1} \;\;\; \mbox{and}\;\;\; y=1/x.$$
A Möbius transformation is itself an example of a rational map, but unlike other rational maps, collections of Möbius transformations can form self-contained structures called groups (see here to find out what a group is). As before with the rational maps, using complex numbers makes it possible to apply a Möbius transformation to a point in the plane, giving you another point in the plane as a result. Thus, when you are faced with a group of Möbius transformations and some initial point, you can look at all the points where these transformations take the initial point, again obtaining a kind of orbit.
Amazingly, the dynamics of such a group of Möbius transformations can generate fractals very similar to those arising from rational maps, separating the plane into an analogue of the Fatou set and an analogue of the Julia set (see this article to find out more).

This image depicts the limit set of a group of Möbius transformations. It looks a lot like a Julia set. This image was created by David Wright and first appeared on Plus in this article.
No mathematician can resist such a tempting parallel, and Sulllivan was no exception. During the 1980s he started a dictionary which translates concepts in the dynamics of rational maps to concepts in the dynamics of Kleinian groups, which are particular groups of Möbius transformations. The work proved foundational in the field, enabling people to prove results in one part of the dictionary using tools developed for the other.
More generally, Sullivan's work on dynamical systems identified universal features and fundamental principles in conformal dynamics, a subfield of the theory of dynamical systems which involves the kind of equations we have looked at in this article.
There is much more we could say about the work of this "charismatic and lively member of the mathematics community," as Alex Bellos put it in his brief biography. "[Sullivan] has moved from area to area, seemingly effortlessly, using algebraic, analytic and geometric ideas like a true virtuoso," says the Abel prize citation, which also describes other aspects of Sullivan's work.
Congratulations Dennis Sullivan!
Further reading
- Maths in a minute: Topology
- Maths in a minute: Complex numbers
- Maths in a minute: The Riemann sphere
- Unveiling the Mandelbrot set
- Fantastic fractals
- A fat chance of chaos
- Maths in three minutes: Groups
- Non-Euclidean geometry and Indra's pearls
About the author
Marianne Freiberger is Editor of Plus. Her PhD was supervised by Shaun Bullett, who conceived of a way of combining the two sides of Sullivan's dictionary, coming up with dynamical systems that behave like a Kleinian group on one part of the Riemann sphere and like a rational map on the other. In her thesis Marianne studied some of Bullett's ideas.