
The Chern Medal 2022: Barry Mazur
This year's Chern Medal has been awarded to Barry Mazur, a mathematician of Harvard University. The medal is awarded every four years at the International Congress of Mathematicians "to an individual whose accomplishments warrant the highest level of recognition for outstanding achievements in the field of mathematics".

Barry Mazur. Photo: Lance Murphey.
Mazur received the medal for his "profound discoveries in topology, arithmetic geometry and number theory, and his leadership and generosity in forming the next generation of Mathematicians".
We were lucky to speak to Mazur in the run-up to this year's Congress which is run as a hybrid event with the in-person part taking place in Helsinki, Finland. He told us an astonishing story of changing perspectives, new directions, and a very personal view of mathematics.
From radio to rubber geometry
Mazur got into mathematics because he loved radio. "The physics of radio, the mystery and magic of that physics, got me hooked when I was 12 years old," he says. At high school he became an amateur radio operator, beaming messages in Morse code to other operators around the world.
"I was fascinated by how this 'action at a distance' could possibly happen, and was dubious about any explanation of it," he says. "I thought of myself as a 'philosopher of electronics', and enrolled at MIT hoping to follow a path that had such a description. But the minute I got there, I discovered that what I thought was 'philosophy of electronics', everybody else called mathematics."
Once he started on maths in earnest, Mazur became interested in objects quite a lot messier than the waves that bring us radio: knots. As we all know from bitter experience, knots have a way of fooling us, shape-shifting in front of our eyes as we try to undo them. They are perfect objects for mathematicians to investigate, not so much because that might help us undo knots in real life, but for the thrill of the study. "Knot theory is so wonderful, if you're into it you get a sense that your geometrical intuition is ever expanding," says Mazur.See here for all our coverage of the ICM 2022 and the prizes awarded there.
The first thing you realise when looking at knots is that their exact shape and size is not what matters. What characterises a knot is to do with the way it is tangled up, not with the way it is laid out in space. Classical geometry, with its precise notions of shape and size, isn't so useful here. What you need instead are the more forgiving notions of topology. This field of maths considers two shapes to be the same if one can be deformed into the other by stretching, squeezing or bending, without doing something dramatic such as cutting the shape or glueing bits of it together. Topology is sometimes referred to as rubber sheet geometry.
Not a knot
Armed with the topological mind set, Mazur ventured on his PhD. The work involved what you could think of as the simplest kind of knot: a simple loop, the shape you get from an untwisted rubber band. You can arrange such a loop on a tabletop in an untold number of ways without breaking its smooth un-knotted structure. And since the loop itself is a deformed circle, the inside and the outside of the loop on the table are just deformed versions of the inside and the outside of a circle — this intuitive fact is made mathematically precise in something called the Jordan curve theorem.
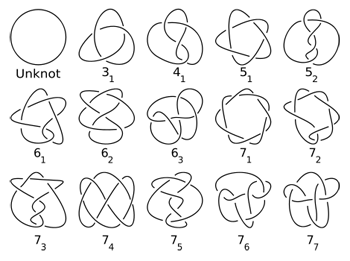
This image shows the so-called unknot (top left) as well as other prime knots which are defined by the number of crossings. Prime knots are knots that, in a certain sense, cannot be considered decomposable. Find out more about prime knots here.
Mazur's PhD work did what mathematicians often do when they have some result in geometry or topology: they ask if it's also true in higher dimensions. The reason they do this is because they can — they have a way of describing higher-dimensional shapes even though they are impossible for us to visualise. Deep mathematical insights often lie hidden in those higher dimensions.
In his PhD thesis Mazur proved a higher-dimensional version of the Jordan Curve theorem, valid for all dimensions. It is often referred to as the Schoenflies Problem. (In three dimensions we can still visualise what’s going on: the problem is about how deformed spheres can sit in surrounding three-dimensional spaces.)
The work produced one of many mathematical notions that now carry Mazur's name: the Mazur swindle. It is called that because it involves a clever mathematical argument that really shouldn't be allowed but, in the setting Mazur was looking at, turns out to be perfectly legitimate. If you fancy some mathematical diversion, see here to get a gist of the swindle.
While really a result in topology, the Jordan curve theorem hints at an approach that is often taken in knot theory: rather than looking at a knot itself they look at a space they imagine the knot to be sitting in, minus the knot itself. This not-knot space can tell you a lot about the knot itself. Mazur helped to develop the deep mathematical insights needed to explore it. Curiously, the approach also led him into an area that has nothing at all to do with knots: number theory.
From knots to numbers
Deceptively simple, number theory is interested in the integers 1, 2, 3, 4, and so on, and their arithmetic. An example of a question a number theorist might ask is whether there are three integers a, b and c, which satisfy the equation
$$a^2+b^2=c^2.$$ In this example the answer is yes. For example, $a=3$, $b=4$ and $c=5$ will do, as $$3^2+4^2=9+16=25=5^2.$$
The prime numbers are particularly important in number theory. They are numbers that can only be divided by themselves and 1, such as 2, 3, 5, 7, and 11. Because they can't be factored into smaller components they are often thought of as the atoms of number theory: if you want to prove something about all integers, proving it for the primes usually goes a long way, as the other numbers will follow suit more easily.

The ancient Greek mathematician Euclid proved that there are infinitely many primes. He is the man with the compass in this painting by Raffaello Sanzio called The school of Athens.
The first few prime numbers are bunched up together quite closely, but as you go up the number line, they become sparser. We know that there are infinitely many primes, but just how they are distributed among the other numbers is still a mystery. It's the subject of one of the biggest open problems in maths, called the Riemann hypothesis (you can read more about this here.)
Number theory is notorious for posing easy-looking problems that turn out to be fiendishly hard to prove. In a beautiful article from 1991 Mazur compared those problems to beautiful and tempting flowers, writing that, "number theory swarms with bugs waiting to bite the tempted flower-lovers who, once bitten, are inspired to excesses of effort".
The flower that tempted Mazur, however, wasn't a simple equation or easy statement — it was an analogy he spotted with knot theory. Mazur realised that if you considered the primes as analogous to knots, and the other integers as analogous to a space that surrounds the knot, then you could adapt the powerful ideas of knot theory to apply in number theory. "The idea of transposing the vocabulary on knots to the vocabulary on numbers was intriguing," he says. "It was not only enormous fun but also a good in-road into the intuition on number theory."
One result of this approach was a proof of the Iwasawa Main Conjecture, which Mazur provided together with Andrew Wiles in the early 1980s. The proof can be viewed as an analogue of the Riemann hypothesis that works in a different setting than the one mentioned above. It also led Mazur to other important results and, crucially, set new directions in number theory.
A famous flower
Proving, or even stating, the Iwasawa Main Conjecture requires deep mathematics we can't begin to explore here. What we can do, however, is visit one of the tempting flowers that have driven generations of mathematicians to excesses of effort. In the example above we found a set of three integers that satisfy the equation
$$ a^2+b^2=c^2.$$ There are in fact infinitely many such sets, known as Pythagorean triples. But what if we replace the exponent of $2$ in the equation by $3$ to get $$a^3+b^3=c^3.$$ Are there integer solutions then? What if we replace the exponent by $4, 5, 6,$ or any other integer $n$? In 1637 the French mathematician Pierre de Fermat had figured out that the answer is "no". When the exponent in the equation is an integer greater than $2$, then there are no integer solutions that are not all $0$. Fermat scribbled in the margin of a textbook that he had found a "marvellous proof" for this fact, which the margin was too small to contain.
It was this scribble that set mathematicians off on a three-century long struggle for a proof of what became known as Fermat's Last Theorem.
As you probably suspect by now, their journey sent them into deep reaches of mathematics that, on the face if it, you wouldn't expect to be related to the problem. One thing that became clear in the 1970s was that another class of equations was going to be important in the study of Fermat's Last Theorem. They are called elliptic curves, given by equations of the form
$$y^2=x^3+ax+b,$$ where $a$ and $b$ are integers.
As you might remember from school, studying shapes like circles or parabolas, is that an equation can also define a curve. Amazingly, the shape of such curves can tell you a lot about solutions to the equations involved and are therefore extremely interesting to number theorists — you can read more in our article about the work of Manjul Bhargava, who won a Fields Medal at the 2014 International Congress of Mathematicians.
Mazur was one of the mathematicians who applied himself to elliptic curves, in fact they play a role in the Iwasawa Main Conjecture mentioned above. Exploiting the beautiful symmetries displayed by solutions that sit on the curves, Mazur was able to prove the so-called torsion conjecture for elliptic curves. Apart from being a result of "supreme elegance and beauty", as the Chern Prize citation puts it, the result initiated new areas of study that helped pave the way for a proof of Fermat's last theorem. This was finally provided in 1994, over 350 years after Fermat's scribble, by Mazur's collaborator Andrew Wiles (see this article for more).
Maths is personal
The Chern Medal is awarded for lifetime achievement in mathematics. What we have touched upon in this article is only a small proportion of Mazur's work.
His prize citation describes him as having a "pluralistic view" of mathematics. "All human beings have some way of approaching the world with mathematical, or near-mathematical sensibilities, intuitions, experience," he said when we asked him what he thought this meant. "And these mathematical approaches and predilections are, in the end, personal, and [can] hardly [be] classified by gross labels."
Mazur is also being honoured for the leadership and generosity he showed to people just starting out in their careers, including the nearly 60 PhD students he supervised. When we asked him what he enjoyed about working with the next generation, his answer was simple: "Most of the time they teach me more than I teach them."
About this article
Marianne Freiberger and Rachel Thomas, Editors of Plus, interviewed Barry Mazur in June 2022.
This content was produced as part of our collaborations with the London Mathematical Society and the Isaac Newton Institute for Mathematical Sciences. You can find all our content on the 2022 International Congress of Mathematicians here.

