Magic 19: Solution

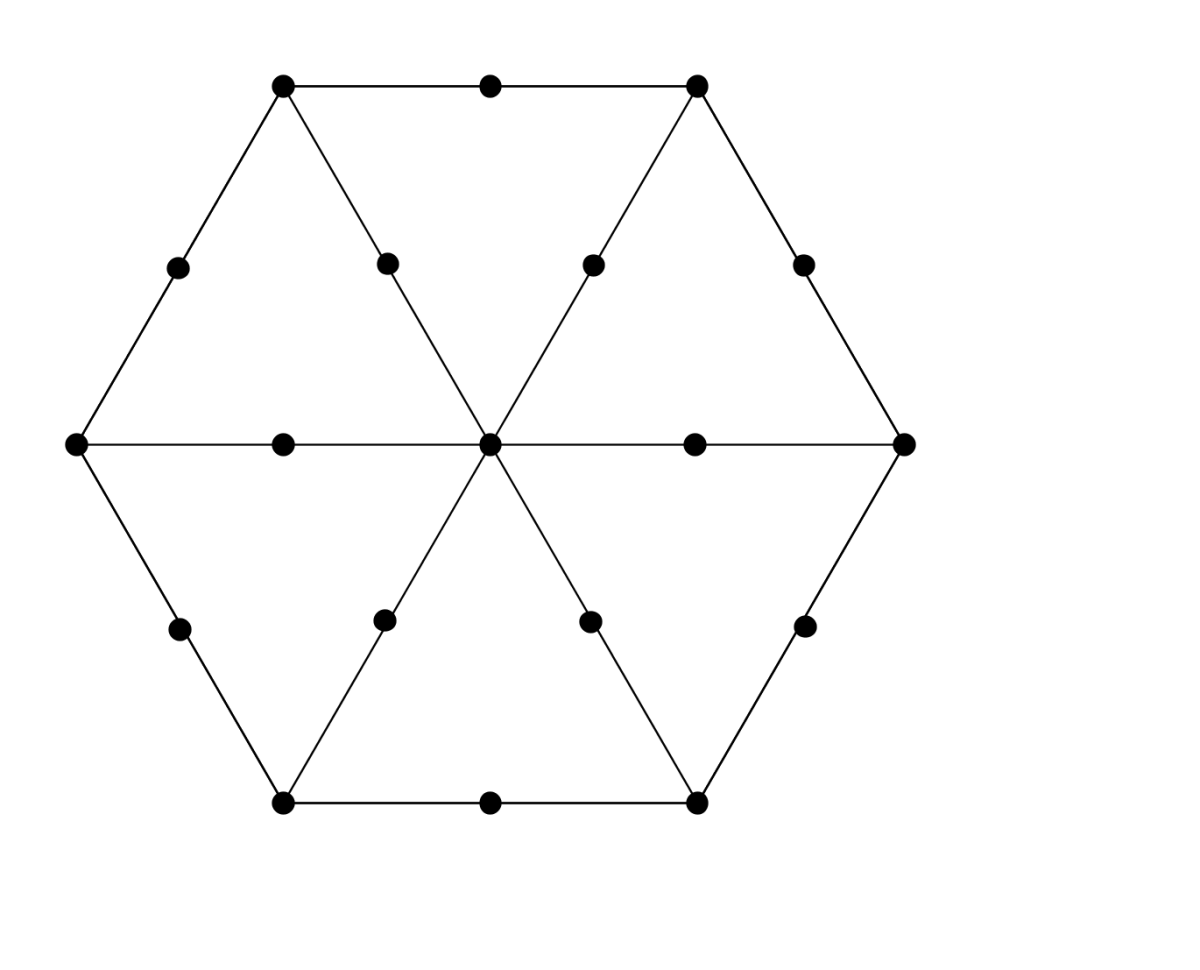
Here are 19 dots arranged in a hexagon. Your task is to label the dots with the numbers 1 to 19 so that each set of three dots that lie along a straight-line segment add up to 22.

Happy puzzling!

(Download the grid to print and scribble on.)

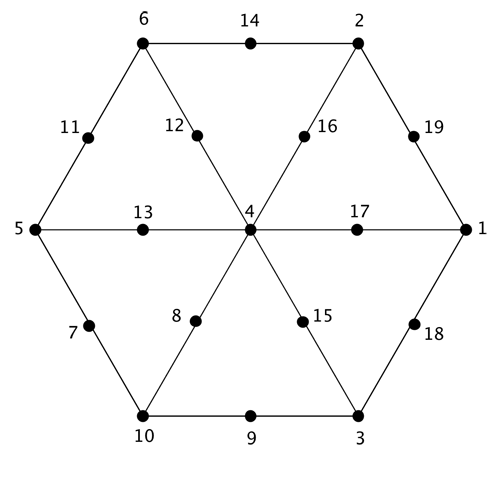
Solution

Here's one solutions. If you have found others, or a good strategy for solving the puzzle, please let us know!

Back to main puzzle page

Add new comment

If x is the central dot, y1

Comment

If x is the central dot, y1 to y6 the dots participating in 3 lines, z1 to z12 the dots only participating in one line, and if A=y1+y2+y3+y4+y5+y6 and B=z1+z2+...+z12, then:

x+A+B=190 (the sum of all natural numbers from 1 to 19)
6x+3A+B=264 (the sum of all 12 lines with a sum of 22)

Therefore:
A=(74-5x)/2 (1)
B=(306+3x)/2 (2)
With x,A,B being natural numbers

Applying to x its possible values, i.e. 1,2,3,...,19 we have:
For x=1, A= 34,5 --> so x isn't 1
All odd values for x give the same result

For x=2, A=32 and B=168. We accept x=2, because in this case A has a minimum value of A=1+3+4+5+6+7=26

Same goes for x=4, since A=27 and B=159, with Amin=24

For x=6, A=22 and B=162, with Amin=22; x=6 is the last acceptable value for x, since:
for x=8, even though A and B are natural numbers, and therefore acceptable values, A < Amin and therefore x>8 is not an acceptable solution. Moreover, x has been shown to be an even number.

However, if x=6, one cannot find any solution when trying to solve the grid. Therefore, solutions are acceptable only if x=2 or x=4.

Love Anonymous' summing approach!

Comment

Beautiful approach. I got the 3 connections at each corner vertex, and 6 in the middle vertex, 1 for every other vertex, too. Then I went on to reason that 19 consists of 10 uneven and 9 even numbers, since 22 is even, and only three even numbers or two uneven and one even yield an even result, I went on to find a configuration on the grid, satisfying this. Which proved to be a tedious effort. However, convinced that this ought to be true, I didn't conceive of the summing up, which as presented by you, proves very elegant.

Thanks for such a logical explanation and method, these magic riddles often have a habit of getting me in a bad mood, for their lack of solving methodology.

A third solution

Comment

This post is from last year, I know, but I just recently discovered this webpage!

I found a third solution in addition to the two mentioned here. It has number 2 in the center and the numbers in the corners are (in clockwise order) 1,3,5,7,4,12.
After limiting down the center number to either 2 or 4 and thereafter checking different possibilities I found the three solutions now mentioned, and I do believe that these are the only possible ones.

One more...

Comment

In fact, there is one more with 2 in the middle, with vertices labelled (4,3,1,7,9,8).

So, recapitulating we have:
with 4 in the middle (6,2,1,3,10,5)
with 2 in the middle (4,3,1,7,9,8); (4,12,1,3,5,7); (5,3,1,8,4,11)

And I think that is!
Best

I used the fact that 22 is

Comment

I used the fact that 22 is composed of either: 2 odds and 1 even OR 3 evens, mapping that on the grid meant putting an even in the middle and the having 2 all even radii and 4 of 2 odds and one even. filling in lead to the first solution. doesn't give you a repeatable method but hey ho

Magic 19

Comment

Look closely: There are 15 sets of 3 dots that lie along a straight line making the puzzle unsolvable as far as i can see.