
The magical mathematics of music
The astronomer Galileo Galilei observed in 1623 that the entire universe "is written in the language of mathematics", and indeed it is remarkable the extent to which science and society are governed by mathematical ideas. It is perhaps even more surprising that music, with all its passion and emotion, is also based upon mathematical relationships. Such musical notions as octaves, chords, scales, and keys can all be demystified and understood logically using simple mathematics.
Pitch: Wave frequencies

Music appears to be transmitted by magic, escaping from your expensive stereo - or a loudly passing car radio, or a guitar-strumming maestro - and accosting your eardrums in one fell swoop. In fact, sound progresses as a wave through the air, and sound cannot be produced without an atmosphere. (Or, as the horror movies would say: in space no one can hear you scream.)
A sound wave creates minute pockets of higher and lower air pressure, and all the sounds we hear are caused by these pressure changes. With music, the frequency at which these pockets strike your ear controls the pitch that you hear.
For example, consider the note called "Middle C" (usually the first note learned in piano lessons). This note has a frequency of about 262 Hertz. That means that when Middle C is played, 262 pockets of higher air pressure pound against your ear each second. Equivalently, the pockets of air arrive so quickly that one pocket strikes your ear every 0.00382 seconds. We can draw a graph by putting an X at every time when a pocket of air arrives:

This graph provides a sort of "picture" of Middle C. By itself, it does not tell us much. However, such graphs provide a new perspective on the relationships between different musical notes.
A basic rule is that higher-pitched notes have a higher frequency, corresponding to more frequent air pocket arrivals. For example, the note Middle G (seven semi-tones higher than Middle C) has a frequency of about 392 Hertz, corresponding to 392 air pockets per second, or a time period of 0.00255 of a second between arrivals:

With the higher note (Middle G), the air pockets arrive more frequently - corresponding to a higher frequency, and thus to more X's in the graph.

If you listen carefully to an ambulance siren or a train whistle, you will notice that the noise sounds higher while the vehicle is approaching, and lower after the vehicle has passed by. This is because the approaching movement compresses the X's together, making them arrive more frequently and produce a higher pitch, while the departing movement stretches out the X's and produces a lower pitch. This is musical frequency in action.
So how does this help us? Well, by using knowledge of sound frequencies carefully, such musical mysteries as octaves and chords can be unraveled.
Double the fun: Octaves
No musical notes fit together better than those which are exactly one octave apart. Pairs of notes like Middle C and High C. Or Middle G and High G. Such pairs arise constantly in popular music, as in the first two notes of the classic Somewhere over the rainbow, or the initial "I'm sing..." of Singing in the rain - or the first two notes of the third line of Happy Birthday.

Often in a symphony, one instrument (like a violin) plays a note one octave above that of another instrument (like a double bass). Piano arrangements inevitably include the same note at different octaves. When improvising in blues or jazz music, it hardly matters which octave you choose to play, just which notes within the octave you choose to play. Notes which are one octave apart sound almost like the same note, or at least a new variation on the same note.
What is it that makes notes one octave apart fit together so well? Consider High C, the note which is exactly one octave above Middle C.

For High C, the air pockets arrive once every 0.00191 seconds. This is precisely half the time period (or twice the frequency) of Middle C. The arrivals of High C are not random, or arbitrary, or picked out of a hat. Rather, they are precisely twice as frequent as the arrivals for Middle C.
This is a universal truth of octaves. Going up one octave is always the same as doubling the frequency. Just as the frequency of High C is twice that of Middle C, so the frequency of High D is twice that of Middle D, and so on. Notes one octave apart are always bound together by this basic relationship.
If we play both Middle C and High C at the same time, then their air pockets fit together in a certain pattern:
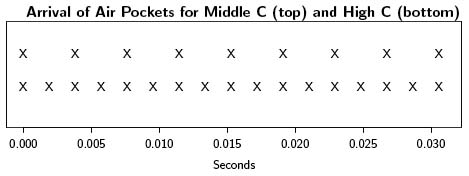
Since the frequency of High C is exactly twice that of Middle C, the two notes line up perfectly. Every two air pocket arrivals for High C correspond perfectly to one arrival for Middle C. The X's for the two notes match up exactly. That is why the two notes fit together so well, and indeed sound almost the same. Their high pressure air pockets arrive in perfect synchronisation.
Similarly, that is why High D fits in so well with Middle D, and indeed why any note fits in so well with the note one octave above or below. In every case, the frequency of one note is exactly twice the frequency of the other, leading to a perfect fit.

One easy way to see this is on a guitar. There, pressing a guitar string at the twelfth fret cuts the string precisely in half. This makes it vibrate precisely twice as quickly. This leads to a frequency which is twice as high, and thus corresponds to a note one octave higher. For example, the first string of a guitar is normally tuned to Middle E. Playing that same string with the twelfth fret pressed produces a High E - a note one octave higher, with frequency twice as high.
The same pattern continues as we increase the octaves. The note two octaves above Middle C (sometimes called High High C) has a frequency four times that of Middle C. And the note an octave above that one, has a frequency eight times that of Middle C. In principle, we could keep increasing the octaves, and doubling the frequencies, forever - but after a certain point, the notes would be so high that only dogs could hear them.
In perfect harmony
Notes an octave apart do indeed fit together well. In a sense, they fit together too well. If you play Middle C and High C together, then there is no discordance at all. However, the result sounds sort of hollow, or even boring. More interesting combinations like chords result if we bring in other notes, too. But which notes sound good together, and which ones don't?
Consider the notes Middle C and Middle G. In fact, these notes form a "fifth" interval and fit together well. But why is this? Well, let's examine their wave graphs together:

We see that every second arrival for Middle C, lines up almost perfectly with every third arrival for Middle G. Once again, the two wave patterns fit well together. The two notes complement each other, rather than clashing. That is why lots of music involves the notes C and G - from the first two notes of the chorus of the traditional song Land of the silver birch, to the first two notes of the Star Wars musical theme.
Since 3 time periods for Middle G correspond to 2 time periods for Middle C, we can also say that the frequency of Middle G is about 3/2 times as large as that of Middle C. Since 3/2 is a nice, simple fraction, that is why C and G sound good together.
By contrast, the notes C and F-Sharp do not fit together well. If those two notes are combined, they don't sound quite right. They rarely appear as a pair in musical compositions or songs of any kind, at least not in a sustained way. A look at their graphs explains why:

This time, the X's just don't line up well. They have no simple relation to each other. The fit just isn't there. (Well, it is true that five time periods for C isn't so far off from seven periods of F-Sharp. But it isn't so close either, and anyway, seven is too large a number of time periods to have to wait.) So, combining C with F-Sharp isn't so great, but combining C with G works well. These fundamental truths apply regardless of your favourite musical style.
Striking a chord
Combining the notes C and G produces a sound which is fine, but not very exciting. To get a really pleasing sound, let's add a third note - E. Middle E is four semi-tones (a "major third") above Middle C, and three semi-tones (a "minor third") below Middle G. When all three notes are played together, they form the "C major chord", which is a sweetly harmonious, happy sound, like a barbershop quartet. It is the basis for music as diverse as Row, row, row your boat, and the symphonies in C Major of Mozart and Beethoven and Schubert.
Why do these three notes - C, E, and G - sound so sweet together? Let's have a look.
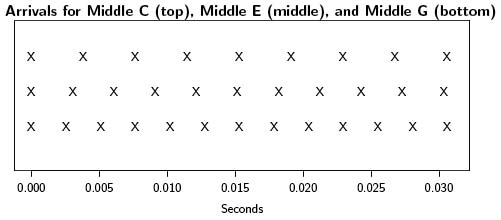
We see that certain of the X's line up almost perfectly. Indeed, 4 time periods for Middle C, and 5 time periods for Middle E, and 6 time periods for Middle G, are all practically equal. So, about once every 0.015 seconds, the X's all line up.
So, even though certain of the X's do not line up for these three notes, quite a number of them do. This combination of variety and consistency is just what is required to produce the C Major chord - one of the most pleasing sounds known to humanity, and the basis of multitudes of tunes from Mendelssohn to Metallica.
So, humanity's quest for beautiful music amounts to finding creative and interesting ways to line up the air pocket X's of different musical notes.
Temper, temper

So why is it that the notes C and G fit together well, but the notes C and F-Sharp do not? Who decides which notes will have their X's line up well, and which notes will not? The answer is, mathematics decides!
Remember that High C has a frequency which is twice as large as Middle C. On the other hand, High C is twelve semi-tones above Middle C. There are eleven other notes - C-Sharp, D, D-Sharp, E, and so on - squeezed in between Middle C and High C. What are their frequencies? How do they fit in?
Early musicians - as far back as the Greek mathematician and musician Pythagoras of the sixth century B.C.E. - tuned musical instruments specially for each key. For example, when playing in the key of C, the note Middle G would be tuned so that its frequency was exactly 3/2 times that of Middle C. This would make the X's line up perfectly, so the notes would fit together exactly right. However, this system required different tunings depending on which notes you were planning to play, or in which key your music was written.
Over the last couple of hundred years, a more universal system has been used instead. This system - called equal tempering, a version of well tempering - spaces all twelve notes of the octave equally. In this way, a single tuning can be used regardless of the key being chosen, or the music being played.
Equal tempering is a system for breaking up each octave into twelve equal semi-tones. Since each octave represents multiplying the frequency by a factor of 2, each semi-tone represents multiplying the frequency by the twelfth root of 2 - a number which produces two when twelve copies are all multiplied together. This number is about 1.059463, because twelve copies of 1.059463, all multiplied together, is equal to 2.
So what does this mean? If we start with Middle C as a base, then Middle C-Sharp, one semi-tone above Middle C, has a frequency which is 1.059463 times as large as Middle C. Then Middle D, two semi-tones above Middle C, has a frequency which is 1.059463 multiplied by 1.059463, or 1.122462, times as large.
Continuing in this way, we eventually reach Middle G, seven semi-tones above Middle C. The frequency of Middle G is 1.498307 times that of Middle C.
But wait. 1.498307 is almost exactly the same as 1.5, or 3/2. This explains why every three time periods for Middle G, correspond to two time periods for Middle C. The two frequencies have a nice simple ratio, 3/2, and that is why they fit together so well.
Similarly, the frequency of Middle E is 1.259921 times that of Middle C. This ratio is very close to 1.25, or 5/4, and explains why every five time periods for Middle E correspond to four time periods for Middle C. Hence, like G, the note E also fits in well with C.
Another good example is the note Middle F, whose frequency is 1.334840 times that of Middle C. This is very close to 1.333333, or 4/3. And, indeed, C and F also fit well together (their interval is called a "fourth").
On the other hand, Middle F-Sharp has a frequency which is 1.414214 times that of Middle C. The number 1.414214 isn't too close to any nice simple fraction (it isn't too far away from 1.4, or 7/5, but numbers like 7 are too large to be of much help). That is why the notes F-Sharp and C do not fit well together.
So, to figure out which notes fit well together, we don't need to guess, or use trial and error, or study musical theory for years. We just need to remember the equal-tempering principle, and multiply copies of 1.059463 together to see whether or not we get a simple ratio of frequencies.
Unlocking the key

Experienced musicians are always discussing what key to play in. There is no cooler moment for a jazz musician than, when asked if they can play I got rhythm, to be able to reply, "Sure, dude. What key?"
Changing a song's key raises or lowers all the notes by the same amount. This change might make the song more convenient to play on a particular musical instrument, or more comfortable for a vocalist to accompany. If done properly, the key change should have essentially no effect on the way the song "sounds" - it should be just as recognisable, just as lovely, and just as catchy, in the new key as in the old. Indeed, it should be exactly the same song, just performed at a higher or lower pitch.
How can this be? How can a song be the same, but different? How can we change the pitch without changing the tune?
From our understanding of frequencies, the answer is clear. To make the notes higher (say), we make their frequencies faster, i.e. make the X's closer together. But to make the song sound the same, we leave the relationships between the X's just as they were before. We compress each row of X's by exactly the same factor. Equivalently, we raise each note by exactly the same number of semi-tones.
For example, suppose you are playing a song in the key of C, and are using a C Major chord, with the notes C, E, and G as before. You then want to change to the key of E, and use an E Major chord instead. How do you do this?
Well, to change Middle C to Middle E, you have to raise the note by four semi-tones, or equivalently multiply the frequency by 1.259921. So, to preserve the sound of the chord, you have to do exactly the same thing with the other two notes. Middle E also gets raised by four semi-tones, with frequency multiplied by 1.259921, to turn into Middle G-Sharp. And, Middle G gets raised by four semi-tones to High B. The resulting air pocket arrivals look like this:
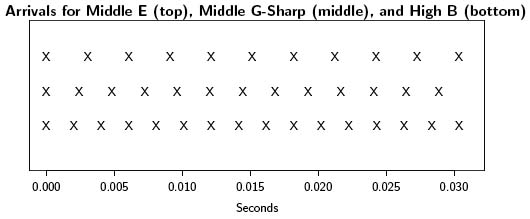
We have thus created a chord E Major, which is just like C Major, except four semi-tones (or a factor of 1.259921) higher. The E Major chord sounds just as sweet, just as pleasing, as the C Major chord we saw earlier. The only difference is, the E Major chord has a somewhat higher pitch. We have successfully switched keys, from C to E.

There are many similarities between this E Major chord (consisting of E, G-Sharp, and B) and the previous C Major chord (consisting of C, E, and G). In each of them, every four spacings in the top row, and every five spacings in the middle row, and every six spacings in the bottom row, all line up well. So, every little while, the X's for all three rows are practically on top of each other. This is why the two chords have the same pleasing sound.
On the other hand, for E Major this confluence happens faster. While for C Major the X's line up about once every 0.015 seconds, for E Major they line up about once every 0.012 seconds. That is why E Major - while sounding similar to C Major in every other respect - also sounds somewhat higher, a fact the vocalist might well appreciate.
So the next time you are accompanying a beautiful starlet in her triumphant performance of her new jazz hit, and she turns to you and says with a wink, "Let's do it in the key of E instead of C this time", don't panic. Simply raise all of your frequencies by a factor of 1.259921, and wait for the audience's wild applause.
About the author

Jeffrey Rosenthal is a professor in the Department of Statistics at the University of Toronto, and is an amateur musical performer who plays several instruments. His book Struck by Lightning: The Curious World of Probabilities is being published in September 2005 by HarperCollins Canada.
Comments
Anonymous
Just want to say thanks to the Author of this page it is very clearly explained and very helpful.
Anonymous
This article is excellent. Thank you.
Anonymous
amazing...........very simple yet informative.................really helpful......:)
Anonymous
I think you will find that Galileo's contribution to Harmony (1623) was anticipated by Kepler in 1619. These works are not easy to find.
Anonymous
Thank-you, thank-you, thank-you.
I can't figure something out unless I understand the why, and learning the guitar has been driving me crazy. This is awesome.
Matt
Anonymous
this page helped me complete my research project. there is some excellent information here. thanks a lot!!!!!!!
Anonymous
I have been reading page after page on why certain intervals correspond and such but I didn't really get it until I read yours! I can't thank you enough! I literal let out a huge ohhhhhhh when I was reading your page! It made everything click! Thank you so much for taking the time to write this! You can't even begin to understand how helpful this has been! :D
Anonymous
One of the most fundamental part which is missing in most music books is precicely the topics provided in this web sitr. Congratulation and thanks. Now I suggest we go further and analize music in terms of numbers. A tempered chromatic scale means there is no flat or sharp notes, but instead, there is a group of musical notes each one of equal importance, it is like a stair with the same steps no matter how high or how low we are in the stair. If we keep constant the number of crhomatic steps between two musical notes then we maintain the type of musical interval. The same applies when dealing with a bigger group of musical notes (a chord). I learned and analyze music in terms of numbers. A "Maj" chord for me es just (4,3) which means you play the tonic ( the lowest note in this particular case), then you move 4 chromatic steps higrher and play the resulting note, and finally go 3 steps further and play the third note, and there you have...a major chord. The most common chords are of course: (4,3), (3,4), (2,5), (5,2), (4,3,2), (3,4,2), (4,3,3), (3,4,3), (4,3,4), (4,4,3), ... do you want to go further...then do this: Make a list of numbers by using only numbers 3 or 4. Ii.e. (3,4,3,4),...... try all possible mathematical combinations priorizing those combiations which do not repeat tonalities....there you have...all chords used in tertial harmony...just play with numbers, just make music by combining numbers, and finally, by algebraical operations among numbers. How many muslcal scales de we have, let say for now, with 7 tonalities per octave ? the number of mathematical solutions is ( 12 above 7 )= 7 ! / ( 12 ! * ( 12 - 7 ) ! ) ( note that n ! = 1 x 2 x 3 x 4 ...x n ). I trully recommend to think in numbers when you think in music. Consonance and dosonance, order and disorder, ..both can represented as number values and sorted by number values ( increasing or decreasing ).
my email is goodrock.producciones@gmail.com for further comments. Regards and thank you for this exellent web page !!!
Anonymous
I enjoyed your article. One thing I don't understand is why of sound travels as waves, two notes played together form chords instead of averaging to give the sound of the frequency in between. For example why doesn't playing A# and C of the same octave sound the same as B. Compare this to light, where combining 2 colors gives the color of light in between (yellow and blue make green).
Anonymous
This is a very good question
For when we hear two pure tones together WE HEAR BEATS
Of course the ear in non-linear - so that explains that! ....... WRONG
Sine (A) + sine(b) is half the sine of A+B plius half the cosine of A-B (or summat like that)
So the "beats" are REAL - in the air - even BEFORE some ear mangles them up.
The astounding BEAUTY of the whole thing is a pure tone AFTER being horribly mangled by our ear STILL SOUNDS GREAT (even if a little dull).
But the nerve signals sent to the brain are HORRENDOUS!
Anonymous
Light waves use superposition. Here's a link to a wikipedia article on superposition and interference.
http://en.wikipedia.org/wiki/Superposition_principle#Wave_interference
Anonymous
Let's just say that anyone with an email address has the ability to alter almost anything on Wikipedia and therefore, is not very trustworthy. In Debating we learn to never trust Wikipedia - and in all reality, should you, as well? Wikipedia is an unreliable source used for approximating information and in the case your point has been proven correct, than perhaps you should have used a more reliable source. And also... Light waves? I thought this was sound frequency.
Anonymous
Wikipedia is a bad source don't trust it
Oliver Lamb
Physics teacher: both light and sound waves are subject to superposition.
This means that when considering what the total wave "looks" like, it might not always be a nice sinusoidal shape. For instance, when combining a wave with another wave twice its frequency, (a note plus its octave; deep red light and very violet light) the resultant wave approaches a sawtooth wave.
Also, although Wikipedia is not 100% reliable, it is a superb source. It is attended to by numerous experts, and typically explains topics excellently.
Anonymous
From my understanding of Physics and Mathematics, a few things take place. All light travels at the same speed, but some light streams have different frequencies then each other. Consider how the brain interprets light signals. An object either absorbs or reflects light, and when light reflects or refracts off of an object at our scale of mass, not planetary or galactic size where gravity takes effect, the angle the light reflects at is the same angle it leaves at. Example: A wall standing upwards at 90 degrees and light from a street light hits it at an agle of 30 degrees. At the point of intersection if you take a perpendicular bisector to the wall so that it is horizontal with the ground, the light travels 30 degrees below that bisector in the opposite direction it came in from. Well this is how our eyes react to light, and given two light streams to produce another is the forming of pure light or white light. Where the speed of light is constant, the speed of sound on the other hand is ONLY constant within the medium it is in. Sound travels faster through gas, than it does water or a preceived to be solid object. The more dense an object the more the acceleration of sound decreases. We have to consider quantum mechanics as well. The actual electrons or charges of the particular atoms that are in that medium comes into play, while sound and friction can almost be interchangeable, either way you look at it they are both virbrations where light is not. The same wave models that represent the electron cloud containing each of its orbitals/electron pairs with their electron spins, "I belive is the effect of sound", causes wave interference. This is why you end up having sounds at different velocities and each sound also has their own frequency as well as amplitude. Light does have frequency like sound, but has no amplitude. I tried to explain this in the easiest way possible. A simple way to visualize this would be speak a word and listen to how long you can here it. It dissapates. Then take a flashlight into a dark room, and turn it on against the wall. (Provided the batteries don't run out), The light will always show against the wall. Your voice litterally travels all the way through the wall and out the building, where as light is reflecting back a percentage of its intensity too you. Some sound does bounce off of objects but sound does move through all mediums. I theorictally believe that sound itselt moves into eternity or infinity, only that it gets smaller and smaller and smaller forever, anotherwords its velcotity and accleration is decreasing as its limit is approaching 0. I believe this because no matter where you look in the Universe 0 degrees Kelvin is only Theoretical. All things are moving hence friction or vibration and there is sound. This is why it is important to watch what you say. The cosmos are recording your voice.
Anonymous
I hope this comment was just a troll/joke.
Light has no amplitude? Are you stupid? No amplitude = nothing. Pure blackness.
You've run around a bunch of silly tangents as well.
Anonymous
I totally agree. Stop spouting tummy-rot on subjects you evidently don't know much on, correct your spelling mistakes and look forward to higher grades in life. "No amplitude"? Are you kidding me?
Buckmeister1
Fact Check!
Sound actually travels faster through water than through air, approximately 4x faster, . 767 mph in air at sea level and 68 deg. F , (344 meters per second at 20 deg. C for our Northern friends.)
Anonymous
Combining Yellow and Blue light does not give green light. It makes white light. Light is additive color mixing. 'Yellow and blue make green' only refers to paint. If i have paint that reflects yellow, in actuality it ABSORBS all other colors besides yellow (subtractive color mixing). So by mixing paints I DECREASE the spectrum of light that is reflected, and get green.
Adding waves isn't as simple as averaging the frequency. Mixing two waves with different frequencies actually gives a wave with two parts: one part that is the average frequency, like you said, and another part that is the difference between the frequencies, which creates "beating."
More here: http://www.acs.psu.edu/drussell/demos/superposition/superposition.html
So yes, the result is a wave that has a frequency similar to a 'B' when you hit those two notes at the same time, but it sounds different because of beating. Real music is also comprised of a bunch of different harmonics and beats, it's not just pure sine waves for each note. So you get a much more complex sound by hitting chords.
Ian777
Our ear is a different machine than our eyes and use different method of analyzing input data. Our ear process the sound waves as mixtures of different frequency (20hz to 20khz) and send it to our brain exactly that: mixture of different frequencies. Our eyes, however, process lights differently than our ear. Two light waves of diffent frequencies will be mappex in our brain as average of the two frequencies. Thats why color mixing works.
Anonymous
Nice article. Well written. I feel inspired to learn more.
Anonymous
Very clear explanation; thanks a lot.
If anyone can add something about a string wave (which cameras can photograph), and what is an overtone, would sure appreciate.
Anonymous
Well done. I am a long since accomplished musician and have known these things for some time. Just as one of your other readers said about knowing the whole thing, I must agree. I have been struggling with Precalculus and its seem to have to do with the inability to switch over my problem solving skills with the guitar to math. The math training has helped my guitar playing tremendously and I was pretty talented before hand. The study of lifting (x) value zeros from polynomials has pushed a natural technique shift into using hammering open notes back to the root note for the respective key. An example would be the D to open E relation ship within descending riff at the end of "Extreme's Hole Hearted." chord progression. Before the math training I was perhaps playing it correctly, now I play it intelligently. You have a unique ability to explain simplicity along side complexity. Excellent work sir. Make some money at it.
Rob
Anonymous
How do you make those frequency graphs?
Anonymous
wow, i sure got lucky, hit your article first. i was wanting to know the mathematical breakdown of notes on a scale. why and what progression of spacing does a luthier put the frets on a fingerboard? trying to understand better the reasoning for the layout of harmonicas. i understand things governed by the laws of nature clearly,(math, physics, ect.). it's things like "English", or languages,created by man than
t confuse me. thanx. now i get it.
Anonymous
thank you, Jeffrey, for explaining in simple, pleasing terms what I have failed to be able to appreciate in other forms.
Anonymous
This is brilliant. I've never really understod frequency in general, and wanted to find what the relationship was between different notes. My daughter studies music and I love this secret language and wondered how everything just works. This is so clever and really clearly explained. Thank you =)
Anonymous
Is that why the "big bang sound waves" traveling thru space arrive at our atmosphere and are recordable? Can the big bang "sound" be recorded in 0 atmosphere? Does it have to hit some atmosphere to be detected again?
Anonymous
This is an excellent article! I studied and played classical piano as a youth for 8 years and I've now worked professionally in the music industry for 26 years. Your article articulated in mathematical but layman's terms what I've known in my heart all along but could not express. Why is music so stirring to the human soul? We are made from the same equations! The groundbreaking gravitational waves just detected in the Cosmos were found to emit a note on our sensors at a humanly perceptible frequency similar to.....you guessed it! Middle C! Gravitational waves as old as the Cosmos itself, 13.7 billion years old. Like seeing a snapshot of the Big Bang itself. And their ghost emits a tone perceived by the human ear and brain as middle C! Music moves humans so deeply because....we are all MADE of the same stuff as the Cosmos itself! I am an atheist and science is the only truth. Thank you for bringing readers closer to the truth.
Kevin
Your comments echo a lot of my own feelings, but with a different conclusion. How we can take something as beautiful as music and convert it to mathematical formulas is truly wonderful. Before reading this excellent article, I had a feeling that harmony in music has been discovered as something orderly that can be explained by mathematics. Order like that does not come into existence by random chance. It strengthens my faith in God the Creator of the universe who alone deserves recognition for these gifts we enjoy.
Anonymous
I must add my appreciation to you Jeff... and a desire to learn more. Thanks to other contributors too for interesting comment :) M
kayla
I've just started music technology and I'm really enjoying it and am so glad I came across your article. But the other day my teacher did this really trippy thing with us. He mentioned a few things Jeffrey Rosenthal did (sine waves, pressure, hrtz, frequencies) but he just played the E note and held it. (he said if we closed our eyes it might help) he then played a B and made us lock onto that note. Then when he played the E again he told us to hear the B within the E note he played. No one else heard it but i'm pretty sure I did. He did it a few times and towards the ending as the E note is trailing off it sort of sounds like the B note? He did this a couple of times and it got clearer and clearer. The other students just looked at us like we were crazy but I could definitely hear it! He then did the same thing but with the G sharp key and I sure as hell was able to pick up that note within the E as well. He then said that's what makes up the E chord. The B and G sharp you could hear within the E, when played at the same time makes up the E chord. He then went on to talk about flattening the G making minors and so on but he'd discuss that later... Anyways, does anyone else know what I mean? I felt this article gave the scientific reason why.
Anonymous
Satisfying. Thanks. :) I have been looking for months out of curiosity. My Physics book didn't help much. Thanks, Sir Jeffrey. :)
Browser
Thanks for writing this up, really helped me!
anonymous
I was wondering if the pitch of the note an octave higher than one before it had a pitch which was double that of the one before it. If you could get back to me that would be great.
Werner
I'm 44 years old and learning how to sing. Maths is an old friend but music is new to me so in learning to sing I'm coming across all these new things that many aren't able to explain and you're left with: that's just the way it is or it just sounds right. Your explanation is clear, to the point and all encompassing. You've taken the voodoo out of music and chords and octaves. It's entirely clear to me now why you need to sing spot-on pitch if you're trying to have a nice sounding voice - slightly off is going to throw Xs out of alignment in many different ways. Thank you, sir!
IvanP
Thank you for the explanation, now i finally can appreciate music in a different perspective. Always wondered why there are different octaves with same repeating notes. And you even explained chords! Separate thanks for that, as I'm trying to learn basic guitar playing and now i know how they work (my mathematician mind is very stiff on music).
Yogesh Raval
Sir,
Why Note E is not so loud as other notes? I have felt that this note E is soft dull. In Indian classical sa re ga m..... E is Komal ga in C scale. I hope that this thing will be satisfied by scientifically and mathematically too.
Anil Grover
Very well explained!!! Thanks.
Arup B
Finally I understand that the fourth is a calculation in frequency of the sound of the key.
Udo Matthias
Cool stuff, i love frequencies and electronic sound music.
udo
Jay Singh
Clearly Explained and Helpful
Thanx
Deborah-May Torrens
Thank you for the information.
I found the content to be interesting and very informative.
The body is like an orchestra. All instruments in the orchestra (cells in the body) need to be tuned to the right note (frequency).
If one of the strings on the violon or keys on the piano are off-key, then the entire orchestra (the body) hears and feels it.
Thank you Teacher. :-D