In maths an invariant of an object is a quantity that stays the same when you make some sort of a change to the object. 

An example from geometry

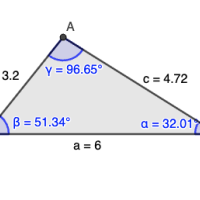
As an example, think about a triangle drawn on a flat piece of paper. You can change the triangle's size by scaling it, that is, multiplying the length of each of its size by the same factor. When you do this, the three angles of the triangle will stay the same. The angles of a triangle are invariants under the operation of scaling the triangle.

You can see this in the Geogebra applet below. Use slider to scale the triangle (multiplying its three sides by the same factor $r$). The angles remain the same.

An example from arithmetic

As another example, think of two numbers $m$ and $n$ with $m>n$. The difference between them is $m-n$. Now add the same amount of $r$ to each of the original numbers to get $m+r$ and $n+r$. Their difference is

$$(m+r)-(n+r)=m-n,$$

which is the same as the difference between the original two numbers. Therefore, the difference between two numbers is an invariant for the operation of adding a constant $r$ to both.

You can visualise this by looking at the numbers as they sit on the number line, as shown in the Geogebra applet below. Use the slider to add the same amount $r$ to both $m$ and $n$ to get $n^{\prime }$ and $m^{\prime }.$ The difference $d$ between the two numbers doesn't change as when you do this.

An example from topology

Like geometry the field of topology studies shapes. But unlike geometry, it doesn't care about the exact values of lengths, angles, and the like. In topology two shapes are considered the same if you can morph one into the other without tearing or gluing. This means  that a perfectly round sphere is considered to be the same shape as a slightly deformed sphere. 

It also means that a perfectly shaped doughnut (technically called a torus) is considered to be the same as a coffee mug. As you can see below, one can be morphed into another without tearing or gluing. 

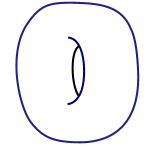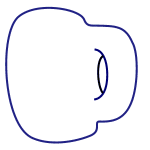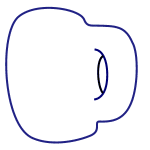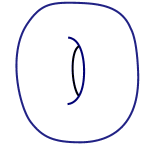
Quantities such as the lengths of lines or the values of angles don't survive this morphing process — their values will change, so they are not invariants. However, one thing that doesn't change is the number of holes a shape has. That's because you can only create a hole by tearing a shape or gluing parts of it together. Hence the number of holes is an invariant under the operation of morphing without tearing or gluing. 

Why do we care about invariants?

Knowing the invariants of an object for a given type of transformation is incredibly useful. For starters, it tells you that you don't need to re-measure or re-calculate the invariant quantity after you've applied the transformation. You don't need to re-measure the angles of a triangle after you have scaled it. You don't need to re-calculate the difference between two numbers after you've moved them along the number line by the same amount. And you don't need to worry about having created or lost holes when morphing a shape without tearing or gluing.

Invariants can also help you identify objects that are related to each other by the transformation in question. For example, suppose you want to find out whether two triangles are scaled versions of each other, but you don't quite trust your eye-sight. If you know the three angles of each triangle, then eye-sight doesn't matter.  If the two sets of angles are the same, then you know for sure that one triangle is a scaled version of the other.

Similarly, the number of holes of a surface, an invariant under morphing without tearing or gluing, gets you a long way in determining its topological type. If a surface has zero holes, just like the sphere, then as long as it is also closed and orientable (see here to find out what these terms means) it is topologically the same as the sphere. 

We can go even further: any closed and orientable surface that has one hole is topologically the same as the torus, any closed surface that has two holes is topologically the same as a torus with two holes, any closed surface with three holes is topologically the same as a torus with three holes, and so on.

 

When it comes to classifying surfaces the number of holes, a topological invariant, plays a starring role!

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.