
Maths in a minute: Optimisation
We all know we need to make the best of things – but how exactly do we do that?
What we need is an area of maths called optimisation, which usually involves maximising something (say the amount of crops we can grow from a field) or minimising something (say the amount of water you need to grow those crops).
Making the best of things
To give an idea of how this might work let's consider the example of a farm somewhere in the tropics in which we want to grow two crops, such as cocoa and pineapples. If $x$ is the amount of cocoa we plan to grow in one year, and $y$ is the amount of pineapples, the unit cost of cocoa seed is $a$, and of pineapple seed is $b$, then the total cost $C$ of growing the two crops is given by
\begin{equation}C = ax+by+d,\end{equation}
where $d$ is the upfront cost we must take on just to use the field in the first place (such as labour, irrigation, pesticides etc). Similarly, when we harvest the crops we might expect a unit return of $e$ on the cocoa, and of $f$ on the pineapples. Thus we might make a profit $P$ given by
\begin{equation}P=ex+fy.\end{equation}
Finally, if the amount of space taken up by a unit cocoa is $g$ and by a unit pineapple is $h$ then the total amount of space $S$ taken up in the field by our two crops is given by
\begin{equation} S = g x + h y. \end{equation}
The problem faced by our farmer is then as follows. They want to grow the right amount of cocoa $x$ and pineapples $y$ which in turn maximises their profit $P$. But at the same time they must also want to keep the cost $C$ below some maximum $C_{max}$, (their total available cash) and require that the space taken up is less than the total area of the field given by $S_{max}$. These two conditions are called constraints. In mathematical terms the problem of maximising the profit becomes:
Maximise $P$ over all positive values of $x$ and $y$ subject to $C C_{max$ and $S
Linear programming
This problem is a special example of a constrained optimisation problem called a linear programming problem. The problem can be solved using a graph. We show an example in which the optimal combination of $x$ and $y$ is highlighted. The horizontal axis represents $x$ and the vertical axis represents $y$. The shaded area is bounded by the lines defined by the constraints and contains values of $(x,y)$ that satisfy the constraints. The optimal combination of $x$ and $y$ occurs at the corner point $A$ of the shaded figure. Perhaps you can work out for yourself why this is the case — if not see here to find out more.
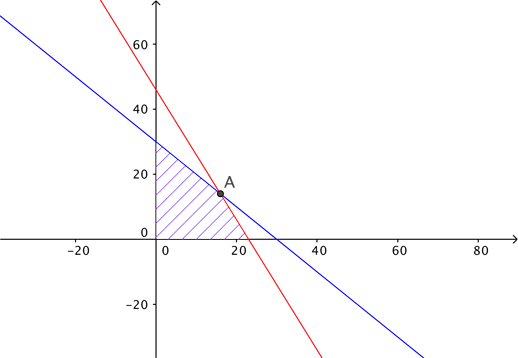
The problem with a=e=g=h=1, b=f=2, and c=4. The optimal combination of x and y occurs at the corner point A of the shaded region.
Generally a farmer will have many more crops, or even animals, to consider, as well as many more constraints, such as labour costs, irrigation costs, and the resistance of each crop to disease and the impact of the weather. This leads to more complex problems similar in form to the one above, but involving many more variables and constraints. A key feature of our problem is that it is linear: we see $x$ and $y$ and their multiples in it, but not more complicated functions such as $x^2$, $x^3$ or $x\times y$.
Remarkably, despite their apparent complexity, there is an algorithm to solve all such linear problems. It is called the simplex algorithm, and its invention in 1947 by George Dantzig was one of the key developments in mathematical algorithms in the 20th century. Today countless optimisation problems are solved by the simplex algorithm, from problems in farming to some of the most complex problems in economics and scheduling.
When the expressions involved are not linear you need to use more complex techniques, such as non-linear programming, but we will leave these for another day!
This is article is edited version of How much maths can you eat? by Chris Budd. You can read more in that article, and in our other content about optimisation on Plus.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
