Maths in a minute: The power of powers

Submitted by Marianne on October 16, 2015

Bored of solving quadratic equations? Can’t be bothered with cubics? Then it’s time to step into the infinite — and marvel at the fact that many of the functions you’ll have come across can be expressed using infinite sums made of powers of $x.$

A great example are the trigonometric functions sine and cosine. It turns out that they can be expressed as follows

  \[ \cos {(x)} = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + ... \]    
  \[ \sin {(x)} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ... , \]    

where $n! = n \times (n-1) \times (n-2) \times ... \times 2 \times 1.$ For both of these series the beautiful pattern continues indefinitely. Choosing a particular value for $x,$ you will find that the infinite series converges to $\cos {(x)}$ and $\sin {(x)}$ respectively.

Similarly beautiful series can be used to express the exponential function $e^ x$ and the natural logarithm $ln(x)$:

  \[ e^ x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3! } + \frac{x^4}{4!} + \frac{x^5}{5! } + ... \]    

and

  \[ \ln {(x)} = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \frac{(x-1)^5}{5} - ..., \]    

though in the case of the logarithm this only works when $0 < x \leq 2.$

Other functions too can be expressed using a power series, also called a Taylor series, and this is a very useful thing: for example, you can approximate the value of any of the functions above at $x$ simply by evaluating the first few terms of the power series.

For example, if your calculator doesn’t have a cosine button and you want to work out $\cos {(1)}$, you can approximate it by:

  \[ \cos {(1)} \approx 1 - 1^2/(2 \times 1) + 1^4/(4 \times 3 \times 2 \times 1) = 1 - 1/2 + 1/24 \approx 0.54. \]    

The following figure shows how the graphs of the functions coming from the first few terms of the power series of the cosine function approximate the graph of the cosine function itself.

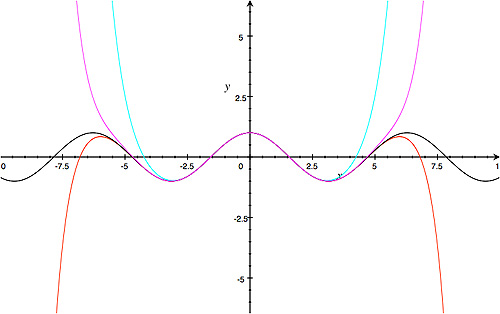Graphs

The black curve is the graph of $\cos {(x)}.$ The cyan curve is the graph of

  \[ f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}. \]    

The purple curve is the graph of

  \[ f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}- \frac{x^{10}}{10!}+ \frac{x^{12}}{12!}. \]    

And the red curve is the graph of

  \[ f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}- \frac{x^{10}}{10!}+ \frac{x^{12}}{12!} - \frac{x^{14}}{14!}. \]    

Comments

Submitted by Anonymous on October 17, 2015

We know that sin(0)=0 ,and if we apply it to the infinte sum of sin(x) we find sin(0)=1 . So why does it not works ?!?

Submitted by Marianne on October 19, 2015

There was a mistake in the formula, which we have now corrected. Apologies for confusing you!

Submitted by Anonymous on October 18, 2015

sin(x) is, of course, not 1 -x^3/3! + ..., as mentioned above, but x - x^3/3!+...

Submitted by Marianne on October 19, 2015

Thanks to the two previous commenters for pointing out the mistake, we've corrected it.

Submitted by Anonymous on October 19, 2015

Shouldn't the expression for sin(x) begin with x, instead of 1?

Submitted by Anonymous on November 3, 2015

I was enlightened by this article, especially after being scared off trig functions at school. I was even more enlightened when I punched in cos (1) into my calculator, a Casio fx-85GT PLUS which does have a cosine button, and got 0.9998... instead of 0.54... After an hour's bafflement I realised I needed to shift the set-up to radians, whereas I'd never got beyond degrees at school. Great, something more I've learnt. Purely as a matter of curiosity though, is it possible to come up with a power series that does as neatly converge on a value in degrees?

Chris G

Submitted by Anonymous on November 4, 2015

Hi, you will see that at x=2 x Pi (= 6.284..) cos(x) has completed one whole cycle; as there are 2*Pi radians in one cycle. There are also 360 degrees in one cycle. Therefore there are 360 / ( 2 x Pi) = 57.295779.... degrees in one radian. Now simply multiply every term in the expansion by 57.3 and you have the result in degrees. Of course it is easier to just use the original expansion and do a single multiply of the result by 57.3.

I hope this helps! Tony S

Submitted by Anonymous on November 8, 2015

Thanks Tony, but I'd already assumed there are so many degrees per radian. What intrigued me was the way that series expressed the cosine function without needing to incorporate any such conversion factor and what was special about radians as opposed to degrees which enables this. In the same vein, I was wondering if there was any similarly elegant and simple series which could do the same for degrees.

Chris G

Submitted by Anonymous on November 6, 2015

Love this article!

Submitted by Anonymous on December 31, 2015

Great insight, Please provide links for further reading and Original geniou/s who gave us this explanation.