Maths in a minute: The power of powers

Bored of solving quadratic equations? Can't be bothered with cubics? Then it's time to step into the infinite — and marvel at the fact that many of the functions you'll have come across can be expressed using infinite sums made of powers of $x.$ A great example are the trigonometric functions sine and cosine. It turns out that they can be expressed as follows $$\cos{(x)} = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + ... $$ $$\sin{(x)} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ... ,$$ where $n! = n \times (n-1) \times (n-2) \times ... \times 2 \times 1.$ For both of these series the beautiful pattern continues indefinitely. Choosing a particular value for $x,$ you will find that the infinite series converges to $\cos{(x)}$ and $\sin{(x)}$ respectively. Similarly beautiful series can be used to express the exponential function $e^x$ and the natural logarithm $ln(x)$: $$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3! } + \frac{x^4}{4!} + \frac{x^5}{5! } + ...$$ and $$\ln{(x)} = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3} - \frac{(x-1)^4}{4} + \frac{(x-1)^5}{5} - ...,$$ though in the case of the logarithm this only works when $0 x \leq 2.$ Other functions too can be expressed using a power series, also called a Taylor series, and this is a very useful thing: for example, you can approximate the value of any of the functions above at $x$ simply by evaluating the first few terms of the power series. For example, if your calculator doesn't have a cosine button and you want to work out $\cos{(1)}$, you can approximate it by: $$\cos{(1)} \approx 1 - 1^2/(2 \times 1) + 1^4/(4 \times 3 \times 2 \times 1) = 1 - 1/2 + 1/24 \approx 0.54.$$ The following figure shows how the graphs of the functions coming from the first few terms of the power series of the cosine function approximate the graph of the cosine function itself. 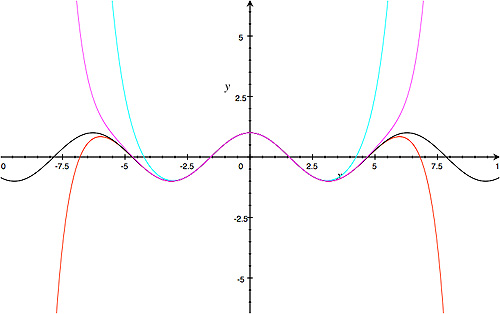The black curve is the graph of $\cos{(x)}.$ The cyan curve is the graph of $$f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}. $$ The purple curve is the graph of $$f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}- \frac{x^{10}}{10!}+ \frac{x^{12}}{12!}. $$ And the red curve is the graph of $$f(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4 !} - \frac{x^6}{6!} + \frac{x^8}{8!}- \frac{x^{10}}{10!}+ \frac{x^{12}}{12!} - \frac{x^{14}}{14!}. $$