Maths in a minute: The Riemann sphere

Submitted by Marianne on October 1, 2013

If you walk around the two-dimensional plane you can keep walking indefinitely in all directions. You could say, in a very hand-wavy and intuitive sense, that there is infinity all around the edge of the plane, only of course you can never get to or see that edge. But still, you could try to imagine what happens if you shrink that infinity-edge to a point. Perhaps this would be a little like tightening the draw string on the rim of a fabric bag. Once you've tightened it, the bag is closed and resembles a deformed sphere.

Stereographic projection. Image: Jean-Christophe Benoist.

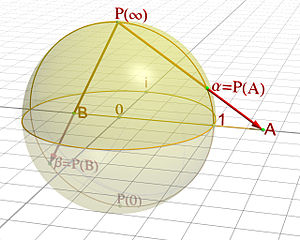
There is a way of making this intuition precise. Imagine a sphere and the plane that contains its equator. For any point p on that equatorial plane, draw the straight line that connects it to the North pole of the sphere. That straight line is going to intersect the sphere at some point. If p is on the exterior of the sphere it will intersect the Northern hemisphere of the sphere. If p is in the interior of the sphere the line will intersect the Southern hemisphere of the sphere. And if p lies on the sphere, so it's actually on the equator, it will itself be the intersection point. This way of associating to every point in the plane exactly one point on the sphere is called the stereographic projection.

It's easy to see that the further out on the plane your point p, the closer its projected image on the sphere is to the North pole. But no point on the plane projects to the North pole itself. The North pole is still available and as a sequence of points move out towards infinity on the plane, their projections move towards the North pole on the sphere. So you now declare that infinity is just a point (you draw the drawstring tight) and that its projection is the North pole of the sphere.

What you get is a continuous one-to-one correspondence between your plane together with infinity and the sphere. The two can be treated as one and the same thing. The plane with a point at infinity appended is called the Riemann sphere after the 18th century mathematician Bernhard Riemann (although strictly speaking the Riemann sphere is the complex plane with infinity appended — see here for more on complex numbers).

This is incredibly useful. You are probably familiar with functions that take the number line into itself. An example is $f(x)=1/x:$ it takes a number $x$ from the number line as input and returns $1/x$ as output. Unfortunately, the function is not defined at $x=0$ because division by $0$ is not allowed. However, as $x$ gets closer and closer to $0,$ $f(x)$ gets closer and closer to plus infinity if you're coming from the positive side, or minus infinity if you're coming from the negative side. If you could treat plus and minus infinity as one and the same ordinary point, then the function could be defined at $x=0$ and would be perfectly well behaved there. You can also define functions that take the plane into itself (the complex function $f(z)=1/z$ is an example) and again they may not be defined at every point because you have division by 0. However, by treating infinity as an extra point of the plane and looking at the whole thing as a sphere you may end up with a function that's perfectly tame and well behaved everywhere. A lot of complex analysis, the study of complex functions, is done on the Riemann sphere rather than the complex plane.

Comments

Submitted by Anonymous on April 8, 2015

So I can divide any number by 0 then??

Submitted by Marianne on April 13, 2015

Yes, you can do that on the Riemann sphere, which contains a point we can call infinity. however, division by 0 is still undefined if you are working with the number line or ordinary complex plane.

Submitted by Anonymous on September 20, 2015

This is exactly the kind of explanation I was looking for

Thank you very much

Submitted by Anonymous on October 23, 2015

North pole of the sphere must be vertical to the plane. And the line touching only the north pole would be tangent to the circle, and this tangent would be perpendicular to the radius of the sphere touching that point (North Pole) , which means the line touching the north pole only would be parallel to the plane (I mean to the line on the plane vertically below it) and the distance of it from the plane would be equal to the radius, always. So unless the radius of the sphere is equal to 0, or the plane is not flat, the line will never touch the plane, which means there is no point 'infinity' on the plane! Or is it that, that very thing is called infinity? I mean, is the point that never comes infinity?? Or am I wrong?? Is the actual matter quite different????????? Please help....

Submitted by Marianne on October 26, 2015

You are correct. No point on the plane projects to the North pole itself. But as a sequence of points move out towards infinity on the plane, their projections move towards the North pole on the sphere. So you now declare that infinity is a point, though not a point on the plane. It's an additional point. Its projection is the North pole of the sphere.

Submitted by math.nights on March 19, 2016

Arabic: https://goo.gl/N0BBr3

Submitted by polyv3x on October 25, 2016

What would result from the Riemann sphere if it could be reduced to a single point at the northern pole? I guess my question is how to interpret the sphere as it collapses to a point, and then becomes a plane with orthogonal projections?