Maths in a minute: Tiling troubles

Out of all the regular polygons there are only three you can use to tile a wall with: the square, the equilateral triangle, and the regular hexagon. All the others just won't fit together.

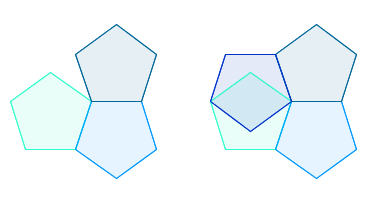
Trying to fit pentagons around a point.

It’s quite easy to prove this. A regular polygon with $n$ sides has interior angles of

$180\frac{n-2}{n} \mbox{ degrees.}$

Suppose you try and make a tiling by fitting several copies, say $k$ of them, around a point so that they all meet at a corner (see the image above). Then the $k$ angles must add up to 360 degrees. If they add up to less there will be a gap, and if they add up to more then copies of the polygon will overlap.

So we need

$k \times 180\frac{n-2}{n} = 360,$

which means that

$k = \frac{2n}{n-2}.$

The term on the right hand side can be rewritten to give

$k = \frac{4}{n-2}+2.$

Since $k$ is a whole number (the number of copies of the polygon you are fitting together), this means that $4/(n-2)$ must also be a whole number. Therefore $n-2$ can only be equal to 4, 2, and 1, which means that $n$ can only be equal to 6, 4, and 3.

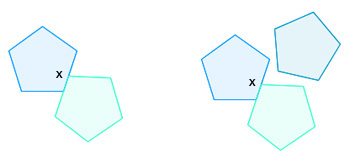
Trying to fit a third polygon with two copies offset against each other.

You could also try to make a tiling in which a corner of the polygon does not necessarily meet the corner of a neighbouring copy, but sits at some point $x$ along the neighbouring copy’s side. That neighbouring copy would therefore have an interior angle of 180 degrees at $x$ (since $x$ is in the interior of one of its sides). To make a tiling you would have to fill the remaining 180 degrees with $k$ copies of the polygon, so you would need

$k \times 180 \frac{n-2}{n} = 180.$

Using a similar argument as above you can convince yourself that this only works when $n=3$ or $n=4.$

You can read more about tilings on Plus.

Maths in a minute: Tiling troubles

Comments

Tiling a wall and polygons

translation

Non Regular Pentagons