Maths in a minute: Triangle central

How do you balance a cardboard cut-out of a triangle on a pencil? Trial and error is one way, but maths can save you lots of bending down and picking it up. Take the pencil and a ruler and connect the mid-point of each side to the opposite corner. You'll find that the three lines intersect in a single point, which lies exactly a third of the way from the midpoint of each side to the opposite vertex. That point, called the centroid, is the centre of mass of the triangle. If the triangle is made from uniform material, so it's not more lumpy in some places than in others, then the centroid is the unique point on which you can balance it without it tipping over. Amazingly, the centroid would also be the centre of mass of the triangle if its mass was concentrated only at its corners, and evenly divided between them.

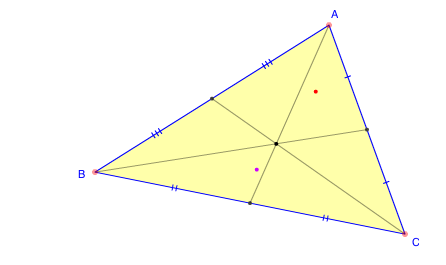
The centroid of a triangle. Image created using an interactivity from Math Open Reference.

Instead of drawing a line from the mid-point of a given side to the opposite corner, you could also draw the line which passes through the mid-point but forms a right angle with the side the mid-point is on. If you do this for each side you again get three lines, and again these meet at a single point, called the circumcentre of the triangle. If you now draw a circle with the circumcentre as its center passing through one of the triangle's corners, you will find that the other two corners of the triangle lie on the circle too! The circumcentre of the triangle is also the centre of the unique circle that contains the three corners of the triangle. But it doesn't need to lie inside the triangle — in fact, it only does if all the triangle's angles are less than 90 degrees (so the triangle is acute). If one angle is greater than 90 degrees (the triangle is obtuse) then the circumcenter lies outside the triangle, and if one angle is exactly equal to 90 degrees then it is the mid-point of the hypothenuse.

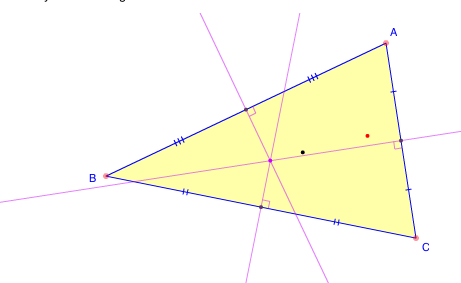
The circumcentre of a triangle. Image created using an interactivity from Math Open Reference.

But there's another point that qualifies as a centre of a triangle. You find it by drawing aline from each corner that is perpendicular to the opposite side. Amazingly, the three lines again meet in a single point, called the orthocentre. As for the circumcentre, the orthocentre lies inside the triangle if the triangle is acute and outside it if it is obtuse. If one of the angles is exactly equal to 90 degrees then the orthocenter will be one of the corners.

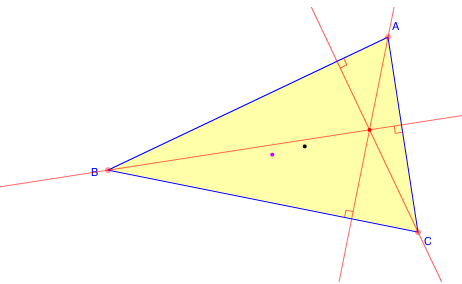
The orthocentre of a triangle. Image created using an interactivity from Math Open Reference.

And what links all these points together? A straight line! The beautiful fact that the centroid, circumcentre and orthocentre of a triangle all lie on a straight line was first noticed in the 18th century by Leonhard Euler, one of the most prolific mathematicians of all time. That line now carries his name: it's called the Euler line of a triangle. You can play around with the three different centres and the Euler line on Math Open Reference which has beautiful interactive demonstrations, from which we made the images illustrating these articles.