The numbers 6, 28 and 496 are perfect. But are they the only ones?

Centuries before the invention of calculus, mathematicians began investigating the properties of and relationships between whole numbers. As such, the study of these numbers, a branch of mathematics now known as number theory, remains one of the oldest mathematical discipline. It has a rich history full of deep and fascinating questions, many of which remain unsolved centuries later.

One such question involves perfect numbers. A perfect number is a whole number which equals the sum of its proper divisors: for example, $6$ is divisible by $2,3$ and $1$ and is also equal to the sum $1+2+3=6.$ Similarly $28$ is divisible by $1,2,4,7$ and $14$ and equal to $1+2+4+7+14=28.$ Indeed, perfect numbers fascinate mathematicians and non-mathematicians alike because their understandable definition contrasts with their complexity and mystery.

Perfect numbers and Euclid

The story of perfect numbers began over twenty-three hundred years ago in one of the most influential mathematical works ever published: The Elements. Born around 300 B.C., the Greek mathematician Euclid founded the study of perfect numbers as a teacher at Alexandria under the reign of Ptolemy the First.

Though often thought of as strictly a geometer, Euclid studied many branches of mathematics, and number theory certainly failed to escape his grasp. In the final proposition of chapter nine of Elements, Euclid proves that

If any multitude whatsoever of numbers is set out continuously in double proportion, (starting) from a unit, until the whole sum added together becomes prime, and the sum multiplied into the last (number) makes some (number), then the (number so) created will be perfect.

Let's pick this rather complicated statement apart using an example. Starting from the number $1$ (a unit) we multiply subsequent numbers by $2$ (continuously in double proportion) to obtain a sequence of numbers $1, 2, 4, 8, 16$. Upon adding these numbers together, we arrive at the prime number $1 + 2 + 4 + 8 + 16 = 31$ (a prime number is a number which is only divisible by itself and $1$). Euclid's result says that the sum $31$ multiplied by the final number in the sequence, $16$, will be perfect. That is, $31\times 16 = 496$ should be perfect.

This is true: the divisors of $496$ are $248, 124, 62, 31, 16, 8, 4, 2$ and $1$ and $$1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248=496.$$ In fact, $496$ is the third perfect number, after $6$ and $28$.

Euclid's incredible result inspired generations of subsequent mathematicians, as it provides a sure way of discovering new perfect numbers. There is a sticking point though: to get a perfect number at the end, the result of the sum (in our example $31$) must be a prime number. But this isn't always the case, and checking it requires a substantial amount of computation. Even today, mathematicians obsess over ways of identifying new prime numbers because it's far from easy.

Perfect numbers and Nichomachus

The next major player in our story goes by the name of Nichomachus. Another Greek philosopher, Nichomachus lived around 150 A.D. and was a leading member of the school of thought started by the famous Pythagoras. Unlike Euclid, Nichomachus felt little need to provide rigorous proofs of his results, though he asserted their truths nonetheless.

According to Nichomachus, non-perfect numbers are somewhat monstrous.

Thus, his impact on perfect numbers lies, not in neat propositions, but rather on the classification of numbers — which he presented in his work Introduction to arithmetic — as either abundant, deficient or perfect.

According to Nichomachus, a deficient number $n$ is a number whose proper divisors sum to something smaller than $n$, an abundant number $n$ has proper divisors which sum to something larger than $n$, and — as we have seen — a perfect number $n$ has proper divisors whose sum is precisely $n$. Naturally, every number will fall into one of these three categories.

Nichomachus not only classified numbers in this way, but also argued that deficient and abundant numbers are of lower quality than their perfect counterparts:

In the case of the too much, is produced excess, superfluity, exaggerations and abuse; in the case of too little, is produced wanting, defaults, privations and insufficiencies. And in the case of those that are found between the too much and the too little, that is in equality, is produced virtue, just measure, propriety, beauty and things of that sort — of which the most exemplary form is that type of number which is called perfect.

Indeed, subsequent thinkers often followed Nichomachus's classification, treating perfect numbers as having a certain divine quality. For example, the fourth-century theologian Saint Augustine wrote in The City of God that "Six is a number perfect in itself, and not because God created all things in six days; rather, the converse is true. God created all things in six days because the number is perfect".

As another example, Hrotsvit, a tenth-century German poet, refers to perfect numbers as "the principal numbers" and even discusses the first four —  $6, 28, 496,$ and $8128$ — in her play Sapientia. Therefore, Nichomachus began a tradition of deifying perfect numbers which, in its own way, continues even today.

Perfect numbers and Ibn al-Haytham

Over twelve hundred years after the death of Euclid, we travel to the Middle East for another result on perfect numbers. The Persian mathematician Ibn al-Haytham studied a wide variety of fields, ranging from physics and optics to number theory and geometry. In particular, he voraciously studied Euclid's Elements as a case study for mathematical methods.

As far as perfect numbers were concerned it appears that Ibn al-Haytham was the first to suggest that the converse of Euclid's proposition was also true: that Euclid's process for generating perfect numbers in fact produces all perfect numbers that are even (to find out why they are all even, see the next article in this series). Although Ibn al-Haytham wasn't able to fully prove this result, he was the first mathematician to attempt a complete characterisation of all even perfect numbers. Many subsequent mathematicians attempted to emulate Ibn al-Haytham's work, hoping to make additional progress, but the world had to wait an additional seven hundred years for a full characterisation to emerge.

Perfect numbers and Euler

Leonhard Euler, 1707-1783. Portrait by Johann Georg Brucker.

Born in 1707, Leonhard Euler remains one of the most prolific mathematicians to have ever lived. Indeed, almost every field of mathematics bears a result with his name, and number theory is no exception: Euler finally proved that Euclid's algorithm for producing perfect numbers in fact produces every even perfect number.

As such, even perfect numbers are in exact one-to-one correspondence with primes of the form introduced by Euclid. In addition, Euler identified the eighth perfect number — the first new perfect number to be discovered in two hundred years:

$$(2^{30})(2^{31}-1) = 2,305,843,008,139,952,128.$$

Considering the long periods of time that elapsed between discoveries of perfect numbers, some mathematicians lost faith in the idea that more would ever be discovered. Indeed, Peter Barlow wrote, in An elementary investigation of the theory of numbers, that

[Euler's perfect number] is the greatest prefect number known at present, and probably the greatest that ever will be discovered; for, as they are merely curious without being useful, it is not likely that any person will attempt to find one beyond it.

However, Peter Barlow died in 1862, just twenty-one years before the discovery of the ninth perfect number. Advances in number theory and — later — a new technological era, made identifying unimaginably-large perfect numbers a real possibility.

Perfect numbers today

Fast forward to today. To date 51 perfect numbers have been discovered; the largest has 49,724,095 digits (you can see a list of all of them here). Even more impressive, it has over three million more digits than the 50th perfect number, discovered just one year earlier. This progress results from a powerful partnership between mathematics and computer science, a phenomenon which Figures 1 and 2 illustrate.

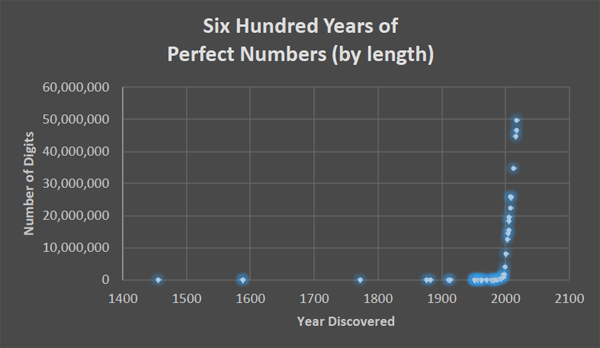
Figure 1: A plot comparing the number of digits to the year discovered of the 5th through 51st perfect number. The spike starting just before the year 2000 marks the introduction of the Great Internet Mersenne Prime Search (GIMPS), a collaboration of thousands of mathematicians which simultaneously runs on almost two million computers.

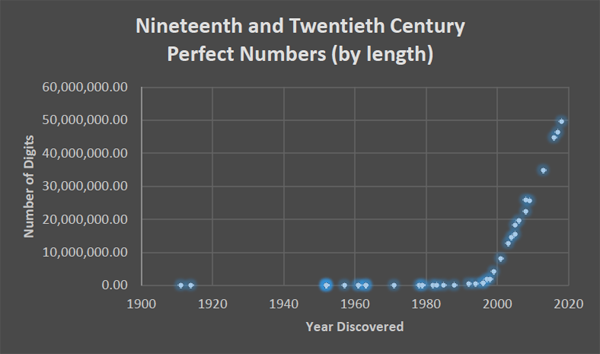
Figure 2: A zoom-in of figure 1, emphasising the development of perfect numbers in the 19th and 20th centuries. Notice that the increased slope in the 21st century represents not more perfect numbers, but rather substantially larger perfect numbers.

Of course, computing perfect numbers remains quite distinct from proving facts about them. Even though we discover new even perfect numbers almost every year, many questions require further exploration:

• What common properties do all perfect numbers, odd or even, share?
• Are there infinitely many even perfect numbers?
• Are there any odd perfect numbers?

Countless mathematicians have chipped away at these questions, with either heuristic arguments or specialised cases. Yet, general answers remain elusive. In the following two articles, Perfectly even and Perfectly odd, we summarise, elucidate, and connect substantial results on these questions, with the ultimate goal of engaging mathematicians and non-mathematicians alike in perhaps the most bizarre definition of perfect.

About the author

Kyrie Johnson is a college student who will be starting a doctorate programme in maths next fall. They are particularly fond of number theory because they adore how some of its most accessible problem statements — such as perfect numbers, Fermat's Last theorem, and the distribution of prime numbers — require intricate and complex solutions. When they're not thinking about number theory, they like rock climbing, listening to music, and playing games.