
Meet the hyperbola
Out of the conic sections, we are most familiar with the circle and its generalisation, the ellipse, and the parabola. To most of us, the hyperbola seems a far stranger beast.
Like the ellipse and the parabola, you can produce a hyperbola by slicing through a double cone. If you think of the double cone as two cones, one balancing vertically above the other on their points, then a circle is created by taking a horizontal slice. Angle your slice and the cross section you create is an ellipse. If your slice is angled parallel to the surface of the cone, then your slice will create a parabola. And finally, if you slice through the double cone vertically you create a hyperbola.
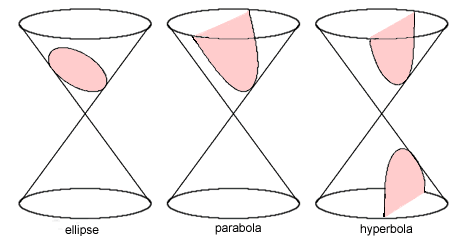
The conic sections (the circle can be thought of a special type of ellipse)
(Image from nrich)
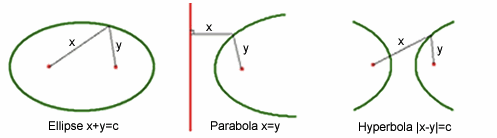
You can also describe all of the conic sections as a locus: a set of points that all satisfy a particular property. A circle is the locus of points the same distance from the centre (the focus of the circle), an ellipse is the locus of points with the same sum of distances from two foci (x+y equals a constant c in the image above), a parabola is the locus of points equidistant from a focus and a straight line called the directrix (x=y) and a hyperbola is the locus of points with the same difference of distances from two foci (|x-y| equals a constant c).
In some ways, you could say that the hyperbola is when the conic sections really get interesting. Unlike the others, the hyperbola comes in two separate matching pieces, each reflecting the other in a line running between them. There is another line of reflection for the hyperbola that runs through the two pieces cutting them exactly in half. The distance along this line of reflection between the two pieces of the hyperbola is called the major axis. The semimajor axis is, as you'd expect, half this distance and is indicated with an a in the illustration below.
The arms of the hyperbola are contained by two asymptotes, the diagonal lines in the illustration below. The arms approach closer and closer to, but never touch, the asymptotes as the hyperbola extends outwards. The perpendicular distance from the major axis to the asymptotes, measured from where the major axis meets the hyperbola, defines what is called the semiminor axis, indicated as b in the illustration below. The minor axis is twice this distance, and lies along the line of reflection running between the two pieces of the hyperbola.
These two numbers, a and b, define the shape of the hyperbola. Any hyperbola can be written as $$ 1=\frac{x^2}{a}-\frac{y^2}{b} $$ using a suitable rewriting of your coordinates. Try altering the values of a and b in the illustration below to see the effect on the hyperbola's shape.
The angle $\alpha$ in the illustration above is the angle the asymptotes make with the major axis, sometimes called the semiangle of the hyperbola. The value of this angle is also given by the values of a and b, as the semimajor axis (a) forms a right-angled triangle with the asymptote, the height of which is given by the semimajor axis (b). Therefore $\tan(\alpha)=b/a$.

A hyperbolic tiling of the disc. Image created by David Wright. (You can read more about this tiling here.)
Hyperbolas lead to many new and intriguing mathematical ideas. Hyperbolic functions are trigonometric functions based on hyperbolas rather than circles. You can define the normal trigonometric functions using a unit circle (that is, its radius is equal to 1). Think of a line from any point on the circle to the centre. Then the cosine and sine of the angle this line makes with the positive x-axis is just the x and y coordinates of the point.
Instead consider a point P on a unit hyperbola (one with $x^2-y^2=1$, so $a=b=1$) and the line passing through P and the centre (which is the intersection of the minor and major axes, the intersection of the asymptotes, and the point (0,0) for the unit hyperbola). Then we can define the hyperbolic cosine (cosh) and hyperbolic sine (sinh) of the angle this line makes with the major axis as the x and y coordinates of the point P.
If you go far enough along this path you end up in an entirely new type of geometry, hyperbolic geometry, which yields many important and beautiful mathematical insights. (You can read more here.) A hyperbola may seem more complicated than some of the other functions you're used to, but it is worth the effort to get to know it better. And you've probably already met one at school: the lovely graph of y=1/x is the first hyperbola most of us meet.
About this article
Rachel Thomas is Editor of Plus.
Comments
Anonymous
Please explain to me the value of angle alpha. Last time I studied Trig the tangent of alpha was sine/cosine which in the illustration would be b/a. What did I miss? Please advise.
Old trig student from long ago
Marianne
Thanks for spotting this mistake! The tangent of alpha is indeed b/a, we have corrected it.
Jay
The Geogebra interactive insert is broken and only says 'Page removed :( This page was removed. Please go to www.geogebra.org!' for me now. Does anyone else have the same problem?
Rachel
Thanks for letting us know - hopefully it is fixed for you now!