James Maynard has been counting prime numbers that don't have the number 7 as a digit. As he informed us at the recent European Congress of Mathematics, he has proved that there are infinitely many of them. The sequence starts with 2, 3, 5, 11, 13, 19, and then carries on forever.

James Maynard.

That's a very cute result — but why? What's the point, and why did the European Mathematical Society see fit to award Maynard one of its prestigious prizes?

The answer is that prime numbers are hugely important in mathematics, and that Maynard's result about primes without 7s is a test case. "Although the prime numbers are on some level very simple, most of the basic questions about them we still don't know how to answer," he explains. "So we're working slowly, developing techniques that will hopefully be able to answer more fundamental questions. [The result about primes without 7s] was a nice test case problem that I have been working on to develop some of the techniques we use to understand prime numbers."

Prime numbers are natural numbers that can only be divided by themselves and 1. Because of this indivisibility they are often described as the atoms of number theory. Every other natural number can be "made" from these atoms in the sense that you can write it as a product of primes. The number 24, for example, can be written as

24 = 2 x 2 x 2 x 3,

and the number 110 can be written as

110 = 2 x 5 x 11.

In a similar way, every other natural number can be written as a product of primes. We have known this since the time of the ancient Greeks, who also managed to prove that there are infinitely many prime numbers. As you go up the number line, you'll never run out of primes.

Many other prime questions, however, remain open. As you move up the number line, the primes appear to become sparser and sparser, but mathematicians still don't know how exactly they are distributed among the other numbers. That question relates to the Riemann hypothesis, one of the most famous unsolved problems in mathematics (see this article to find out more). Another thing you'll find when you look at the sequence of primes is that every now and again they appear to come in pairs that are just two apart: 3 and 5, 5 and 7, 11 and 13, 17 and 19, and so on. These pairs do become less frequent as you look at larger primes, but do they ever stop, or are there infinitely many of them? That's the subject of the famous, and unsolved, twin prime conjecture. (You can see other famous problems relating to the primes here.)

Maynard explaining his result to mathematicians at the ECM in Berlin.

Last year we reported on Maynard's work on gaps between primes. That kind of work inches towards a proof of the twin prime conjecture: if you can prove (as people have) that there are infinitely many pairs of primes that have a gap of 246 between them, then perhaps you stand a chance of improving this result to show the twin prime conjecture is true: that there are infinitely many pairs of primes that have a gap of 2 between them.

Maynard's result about primes without the digit 7 also creeps up on problems like the twin prime conjecture. It's about starting with a set of numbers that have a particular, possibly rare, property (for example not having 7 as a digit) and asking how many of those are prime. The twin prime conjecture can be viewed similarly: start with all numbers that are 2 less than a prime number, and ask how many of those are themselves prime. If you can show that there are infinitely many of them, then you have proved the twin prime conjecture.

As Maynard admits, however, mathematicians are currently pretty "hopeless" at answering these kind of questions. "Finding primes with particular properties, and particularly rare properties, is a very hard problem, which in general we don't know how to do," he explains. "The vast majority of big numbers have lots and lots of 7s in them, so having no 7s is a rare property for any whole number to have." The fact that, despite this rarity, Maynard was able to prove that there are infinitely many such primes counts as an impressive feat. There's nothing special about the number 7, incidentally. Maynard's proof works equally well for any other number: so we now know that there are infinitely many primes without 1 as a digit, or 2 as a digit, or 3, or 4, or 5, and so on.

Prime music and prime pictures

The mathematical tools used to prove such results about primes are a great example of how versatile, and beautiful, maths can be. One of them goes back to the 19th century French mathematician Jean Baptiste Fourier. Fourier was interested, not in numbers, but in the way heat is transferred through a metal plate. He decided to think of the heat source as a combination of regular oscillations, and inadvertently developed mathematical tools for dealing with oscillations — waves — of any kind. Today, the tools that originated with Fourier find many applications in engineering, from descrambling radio signals to digitising music (you can find out more in this podcast).

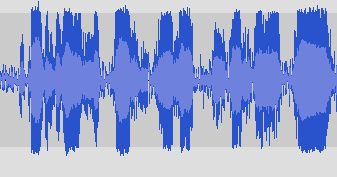
This is what the recording of our interview with Maynard looks like on the sound processing software on our computer. The computer stores this wave form as a list of numbers. The idea of Fourier analysis is to decompose messy wave forms like this one into components representing pure sounds.

But how are they useful in number theory? "It's exactly the same philosophy that engineers use when they employ Fourier analysis to decompose a musical sound into individual notes," explains Maynard. "If someone plays a chord on the piano, then that's actually several different notes superimposed on one another. Fourier analysis is a way of separating these out into individual notes." The idea is that a sound can be represented mathematically — Fourier analysis then decomposed that representation into individual expressions representing individual notes.

It turns out that the mathematical techniques that engineers use when they are studying sound waves can be applied to very abstract pure mathematical problems as well. "I might be interested in the number of primes with certain properties and Fourier analysis gives a way of describing this as slowly changing fluctuations, like waves," says Maynard. "If the number of primes oscillated in a certain way, I'd find this as some 'note' associated to the prime numbers. [The mathematician] Marcus du Sautoy has written a book called The music of the primes which precisely describes this idea of waves being associated to the prime numbers (see this article for more). How loud those individual waves are, and whether they are harmonious or inharmonious, is a very useful way of looking at the primes and allows us to use our intuition about the physical world for purely abstract things."

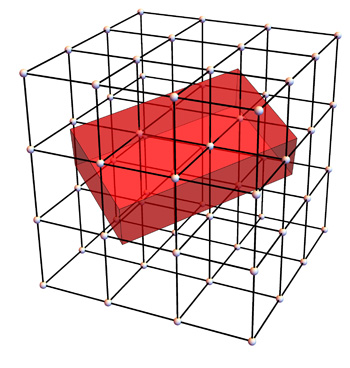
A cuboid sitting on a lattice of points. The number of lattice points inside the cuboid tells Maynard whether there are troublesome terms in his equations.

In another flourish of elegance, Maynard was able to connect his prime music to a picture. It involves a cuboid (an object like a cube, but whose faces can be rectangular rather than square) which sits on a lattice of points. "It turns out that the 'notes' associated to prime numbers were very quiet and didn't cause a disturbance in the equations I was looking at, unless a certain cuboid had unusually many [lattice] points inside it. If a cuboid had many points inside it, then this meant it was possibly the case that these different notes would be much louder and cause lots of problems in my equations." Using the geometric picture, Maynard was able to see what could cause disharmonies in his maths and deal with the problem. It's a beautiful switch from music to pictures.

"This kind of thing is very symptomatic of modern mathematics," says Maynard. "You're quite often tying together lots of different areas of mathematics, and maybe draw inspiration from physics and engineering as well, which normally you wouldn't have thought as associated at all. If you say 'prime numbers' nobody thinks music and nobody thinks cuboids with points in them. But it turns out that all of these things can be related to each other, and this combination of different techniques has proved very useful in mathematics."

Maynard hopes that these different techniques, which came together so neatly for his problem about missing 7s, will also lend themselves to other problems about the prime numbers. So we hope that we'll be able to report on another of Maynard's successes soon.

About this article

Marianne Freiberger is Editor of Plus. She interviewed James Maynard at the European Congress of Mathematics in Berlin in July 2016.