Mouthwatering maths

You'd think a quest for the perfect poppy-seed bagel is one for bakers and chefs, but it's the mathematicians who have made the latest breakthrough. Ed Saff and Doug Hardin, mathematicians from Vanderbilt University, have been working to come up with a new and improved way to distribute points uniformly on various types of surfaces. Not only would this give them a more perfectly appointed bagel, but it would also have applications in computer graphics, explain well known patterns in nature and be an important advance in mathematics itself.

Doug Hardin, left, and Ed Saff (Photo by Daniel Dubois)

Plotting a large set of equidistant points on a flat surface doesn't take a mathematician: any draughtsman can do it. Throw in a curve or two, however, and the problem gets much tougher. For complex surfaces like spheres and bagels (or more mathematically, a torus), it becomes so hard that mathematicians have not found a way to do it with absolute precision. In fact, in 1998 the Fields medallist Stephen Smale listed finding such an arrangement of points on a sphere as one of his Mathematical Problems for the Next Century, saying even an attempted solution was "likely to have great importance for mathematics and its development in the next century".

Hardin and Saff have analysed a method for generating large numbers of points that are spread with near uniformity over practically any surface of any dimension. Their efforts are described in the November issue of Notices of the American Mathematical Society. Their approach assumes that there is a repelling force acting between the points, and then, depending on the strength of the force, positions the points in the most energy-efficient manner (one that minimises the total amount of energy in the system). For example, if the points strongly repel each other, then they tend to spread apart until there is as much distance between them as possible.

In particular, the mathematicians investigated equilibrium cases in which the repelling force between any pair of particles is inversely proportional to the distance between them raised to a power. Their formulation is a generalisation of the inverse square law that is well known in physics, where it describes the behavior of forces such as electrical charge and gravity. In their work, the power depends on a parameter labeled s. Hardin and Saff have shown that when s is small, the points act as if they are responding to a long-range force (like gravity or electromagnetism), and when s is large they act as if they are subject to a short-range force (such as the strong force that binds the atomic nucleus together).

"Think of a room full of people," says Hardin. "In the short-range case, they act like fighting dictators and move until they are spread uniformly around the room. In the long-range case, however, they act as if they are afraid of crowds and end up lining the edge of the room."

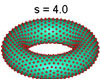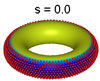
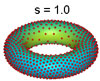
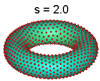
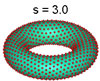
The distribution of points on torus for various values of s
(Illustration by Prof. Rob Womersley, University of New South Wales)

This long-range/short-range behavior is illustrated by the distribution of points on the surface of a torus. In the case of a thousand points, when s is small, the points line up along the outer rim of the bagel and look something like the pattern of treads on a tyre. As the value of s increases, however, the points spread out over more and more of the surface until, for a critical value of s, they reach the stage where they are spread as uniformly as possible. As s increases beyond that critical values the points may move about but the overall uniformity remains the same.

Hardin and Saff have also discovered - and rigorously justified - that this critical value of s is precisely equal to the dimension of the surface to which the points are restricted. In the case of the two-dimensional surface of a bagel, for example, using a value of s greater than or equal to two produces the most uniform distribution of seeds, resulting in the "nearly perfect" poppy-seed bagel. But using a value of s less than two will not spread the seeds evenly.

It could be so much better with just a sprinkling of maths!

The new results extend previous work by Saff and colleagues that focussed on points on the surface of a sphere. Saff and Hardin have extended that work so that it is no longer limited to spherical surfaces, but also applies to elliptical, toroidal, saddle and other two-dimensional surfaces, as well as three-dimensional volumes. Their work can even be applied to surfaces of four or more dimensions.

The procedure has a surprising number of applications. Among other things, it comes in handy when trying to digitise curved surfaces for computer graphics and animations with greater efficiency, in placing the elements of a sonar net on the ocean bottom in the best locations to detect the presence of submarines, and in testing radar systems in aircraft to ensure uniform coverage.

Their theorems also help explain a variety of natural phenomena. They describe some well known patterns such as the distribution of spores on spherical pollen grains and electrons on the surface of a sphere. They also promise to provide new insights into the nature of more complex patterns such as the surface structures of certain viruses and the locations of cracks in crystalline materials. "It's a nice mix of mathematical theory, computation and physics," says Hardin.

The insights provided by this model may be useful in creating new materials on the micron scale with novel physical and electrical properties. The mathematicians are collaborating with physicists Mark Bowick of Syracuse University and Alex Travesset at Iowa State University to explore this possibility. In particular, the researchers believe that an improved understanding of the relationship between certain chemical forces and surface shapes will allow them to create new kinds of thin films and self-assembling membranes which could be useful in certain medical applications.

"I think that we are really at the very beginning of something very big and very exciting that we couldn't see when we looked only at the sphere," says Saff. "Now, if we could only figure out how to design the perfect cheese danish!"