
The origins of fractals
Karl Weierstrass
At the turn of the century hostility was growing between some groups of mathematicians. The cause of this enmity was that certain analysts had shown that functions need not necessarily possess some properties which other analysts thought functions ought to possess. Mathematicians such as Karl Weierstrass were inventing new functions so bizarre as to shock much of the mathematics community. Hermite and his pupil Poincaré in particular described Weierstrass' new creations as "deplorable evil"!
By way of an introduction, we start with a look at the function F(x)=|x|; this has the property that when x>0 then F(x)=x and otherwise F(x)=-x.
Now consider what happens at x=0, shown in the graph below:
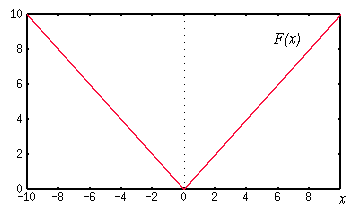
F(x) is continuous by which we mean that there are no gaps in the line. We may consider any continuous function as one which can be drawn without taking your pen off the paper. At the position F(0) there appears to be a "dent" in the line which does not look smooth, no matter how close you zoom in. This is a discontinuity in the slope (or gradient) of the curve as it suddenly changes from one angle to another. At this position the curve is not differentiable as there is no way to calculate the gradient. Being differentiable at a point x is normally defined as looking smooth at that point.
In the late 19th century it was believed that all continuous functions must be differentiable (smooth) in at least one location. It was Karl Weierstrass who proceeded to create a function that was nowhere differentiable, but was still continuous. This means that the gradient of the curve can never be found. A version of Weierstrass' function presented here is based on an infinite sum of cosine curves, and a general case is
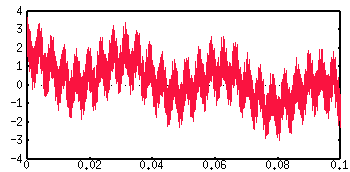
Graph of C(x) against x, where in this case a=8 and b=0.9.
The following sequence shows the curve as an increasing number of cosine terms are added together:
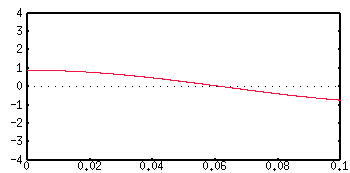
The first term n=1
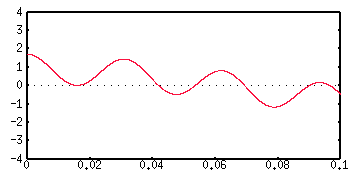
The sum of the first two terms n=1 and n=2
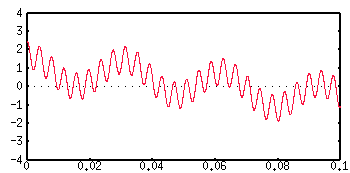
The sum of the first three terms n=1, n=2 and n=3
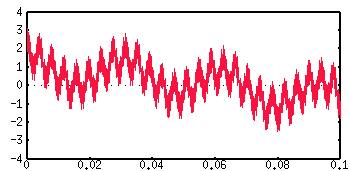
The sum of the first four terms n=1, n=2, n=3 and n=4
At the time there was no conceived use for these functions and many mathematicians were alarmed at losing the property of differentiation as a constant. Hermite described these new functions as a "dreadful plague" and Poincaré wrote
"Yesterday, if a new function was invented it was to serve some practical end; today they are specially invented only to show up the arguments of our fathers, and they will never have any other use".
David Hilbert
Despite these remarks many mathematicians continued to create these "pathological monster" functions and one of the most famous and well used functions was created by David Hilbert. Hilbert was a much respected mathematician at the turn of the century, although his contemporaries such as Gordan often failed to appreciate Hilbert's revolutionary approach to solving problems. This is particularly true of Hilbert's proof of the finite basis theorem which he submitted to Mathematische Annalen, a theorem that Gordan had proved twenty years earlier using a much more computational approach. Today, Hilbert is particularly remembered for his famous 23 Paris problems (which included Goldbach's conjecture - see "Mathematical mysteries: the Goldbach conjecture" in Issue No 2), and also through the concept of Hilbert space, a vital tool in quantum theory.
Hilbert's particular contribution to the "pathological monster" functions has the property of not only being continuous but also surjective, a space filling curve.
Space Filling Curves
The Hilbert space filling curve is created by starting with an initial shape, looking like a staple, that is, copied and rotated four times with connecting lines inserted to fill a square area. Its simplicity and beauty derive from the fact that it progressively subdivides a square array down into an infinite array of sub-squares. The final curve is created by repeating the copying process infinitely many times. The first few stages are shown below.
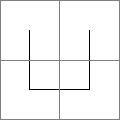 |
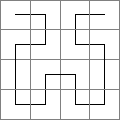 |
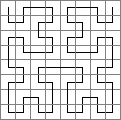 |
 |
This curve is one-dimensional but has the property that it completely fills a two-dimensional space. The corresponding function we will define as H which takes a single real number x and returns a pair of real numbers (u, v) written H(x)=(u,v). This is termed a parametric representation for a curve. It has the following properties:-
- H(x) is a one-to-one mapping (also known as injective) so that if H(x)=H(y) then x=y. This means that the line does not overlap with itself.
- H(x) is onto (also known as surjective) so that every two-dimensional point in the square (u,v) may be expressed as H(x) for some x. This means that the line covers all possible points in the square.
- H(x) is a continuous function. This means that there are no gaps in the line.
Since H is injective, we can find an inverse mapping H-1. Such an inverse mapping would translate a point on the square (u,v) to a value on the line H(x). However, this inverse mapping is not continuous; two neighbouring points on the square, H(x) and H(y) say, will map onto two points x and y on the curve, but these points can be almost any distance away from each other. Since our original function H was continuous, this shows us the important fact that not all continuous functions have a continuous inverse.
Fractals
The term fractal now commonly used to define this family of non-differentiable functions that are infinite in length was introduced in the mid 1970s by Benoit Mandelbrot. The term fractal is derived from the Latin adjective FRACTUS, whose corresponding verb FRANGERE means "to break"; a description which well suits the look of these curves.
To find out more about fractals, take a look at "Modelling nature with fractals" elsewhere in this Issue.
Further reading
The mathematics of fractals is discussed in a few fun web sites:
and in many books including:
- Fractals Everywhere, second edition, by Michael F Barnsley revised with the assistance of Hawley Rising III. Boston; London: Academic Press Professional, c1993
- Computers, Pattern, Chaos and Beauty: graphics from an unseen world by Clifford A Pickover. Stroud: Sutton 1990
- The Fractal Geometry of Nature by Benoit B Mandelbrot. San Francisco: W H Freeman, c1982
Some of the images and text in this article come from the following book:
- Fractal Geometry in Digital Imaging by Martin J Turner, Jonathan M Blackledge and Patrick R Andrews
- Charles Hermite
- David Hilbert
- Benoit B Mandelbrot
- J Henri Poincaré
- Karl T W Weierstrass
- Paul Albert Gordan
Comments
Sean Siegel
Dear Dr. Turner,
I am an undergraduate college student from just outside of Washington, D.C. and I would just like to thank you for your incredible work on fractals. I do not consider myself to be very skilled in mathematics but this is a concept I would very much like to understand and apply to a number of different aspects of life. I have spent the last few months studying infinity and I believe that the mathematics of fractals are critical to helping us understand it. I would love to learn everything and anything more about this subject that I possibly can.