
Light attenuation and exponential laws
Introduction
In 1947 a young Bedouin shepherd found some ancient scrolls while investigating a small opening in the cliffs near the western shores of the Dead Sea. Three ancient scrolls were made from leather, wrapped in decayed linen, and were covered in ancient scripts.

In that same year, Willard Frank Libby of the University of Chicago also discovered Carbon-14, a radioactive isotope of carbon. This led to a method of dating once-living materials by measurements of the radioactivity of the sample. Beta particles (electrons from a nucleus) are emitted when Carbon-14 present in the sample decays into Carbon-12 (the latter is a common and stable isotope) and the rate of these emissions can be measured.
During the following few years, more discoveries were made at four more sites. Hailed as the theological and historical finds of the century, these documents were and still are considered to be of immense importance to Western religion. They have been the source of much controversy, especially since many scholars have been refused access to them in their present place of safe keeping. However, at least one fact could be determined using Libby's Carbon-14 dating technique, which was developed by Libby and his team by 1950 - the age and therefore authenticity of the scrolls.
This dating technique relies on the fact that the number of Carbon-14 atoms released by a radioactive material follows an exponential function when plotted against time. Because of this, radioactivity is said to follow an exponential decay law.
Exponential Laws
Radioactivity is just one of many physical processes that obey an exponential law. Another example, which is a direct analogue of radioactive decay, is radiation attenuation (non-charged particles and electromagnetic radiation) in matter. Newton's Law of Cooling is also an exponential decay law. Likewise, the rate at which electric charge dissipates from a capacitor through a resistor follows an exponential decay law (this has a direct analogy with fluid leaking from a container, where the flow of fluid from the container plotted against time decreases exponentially).
 A planar vibration under resistance gets exponentially "damped out", like ripples from a bobbing fishing float.
A planar vibration under resistance gets exponentially "damped out", like ripples from a bobbing fishing float.The simpler mathematical models of population growth (of bacteria or other animals), where there are no restrictions on food and competition does not exist either within the colony or from outside the colony, give rise to exponential growth models. Populations subject to exponential decay arise in simple life-forms such as viruses subjected to ionising radiation, giving an exponential decrease with increasing radiation dose.
Many other processes and models rely on assumptions which incorporate the ideas of exponential decay or growth in a more involved way (for example the exponential damping of vibrations) and because of this an understanding of exponential relations is a very basic requirement in the sciences and applied mathematics.
Exponential Functions
Arguably, exponential functions crop up more than any other type of function when using mathematics to describe the physical world. For an exponential function y=bax, a general result is that when a>1 the function is a growing exponential function, and when a<1 the function is a decaying exponential function.
Selecting different values of the base value a, there turns out to be only one value of a such that the gradient of the graph is unity at x=0. (This property turns out to be useful in solving differential equations and finding the particular exponential function one needs.) This particular base value is denoted e, and is approximately 2.71828.
Light attenuation
To get a feel for how exponentiality manifests itself physically, let's look at how light (or any electromagnetic radiation, including, for example, X-rays), decays in its brightness (intensity) through a medium.
Consider a thin slice of material. How thin? Well, physically we can't make the slice thinner than one molecule or atom, but we will also put an upper limit on the thickness of the slice: it must not be so thick that any molecule of the substance "lies behind another" taking the line of sight to be perpendicular to the surface of the slice (see the diagram below). We could call this a "no shadowing" constraint. This means physically that the number of atoms per unit volume must not be too large if the "no shadowing" constraint is to be met for our chosen thin slices.
If we took such a thin slice (at this upper bound value of "no shadowing") then we could split the slice even further (into "very thin" slices) where, even if we place several of these behind each other, we will still get no shadowing. So instead of the "thin slice", let us take such a "very thin slice".
![[IMAGE: photons hitting a slice of matter]](/issue13/features/garbett/noshadowing1.gif)
Photons arriving - front view
Now consider the incoming light particles (we will consider light as being made up of particles, and ignore its dual wave nature). We will make the simplistic assumption that if a molecule of material happens to be in the way of an incoming photon, then the photon will be absorbed by the molecule. (This is in fact not that bad an assumption for low-energy photons.) We further assume that the photons are spread out in space randomly in the y-z plane (parallel to the face of the slice) and that the photons travel only in the positive x direction.
Clearly the number of photons absorbed by such a slice depends on the number of molecules in the slice. Of course it also depends on the time interval, so it is better to consider the number of photons absorbed per second as our dependent variable.
![[IMAGE: Photons hitting a slice of matter]](/issue13/features/garbett/noshadowing2.gif)
Photons arriving - side view
Out of six incoming photons in the figure, two are absorbed. This constitutes an attenuation of the beam of photons at the rate of 1/3 per slice. Placing another very thin slice behind the first one would result in twice as many molecules being presented to our incoming photon beam, and we naturally then expect twice as many photons to be absorbed per second (and so removed from the beam). Notice this is true only because of the way a "very thin slice" satisfies the "no shadowing" criterion. Putting three such slices one behind another leads to tripling the number of photons absorbed per second.
![[IMAGE: three very thin slices]](/issue13/features/garbett/3slices.gif)
Photons arriving - side view
Now we use the (almost inevitable) next step, courtesy of the calculus - we take the limit as the thickness of the slice tends to zero:
Now we can write
The relationship
is the differential form of the attenuation law for light transmission. Its particular form is that of the general equation form previously mentioned:
This general form states that: the value of the rate of change of a quantity (here y), with respect to a certain independent variable (here x), is proportional to the quantity itself.
It is exactly this property which leads to a process obeying an exponential law.
The sign of the constant of proportion, c, in the equation above, will determine whether the process is one of growth or of decay.
From earlier, we know a solution to the differential equation above is some exponential function y=bax; or rather, putting this in the standard form for exponential functions,
as expected.
The solution to the attenuation law of light photons can then be written as
We can go further however, since we can easily find (arguing physically) the value of A above.
Clearly, when the beam is at the surface of the material, no photons will have been absorbed (no molecules yet encountered). Thus for x=0 we know that n is the value of photons per second measured at x=0. Call this value n0. Inserting x=0 into the equation above gives us
and so the equation becomes
This last formula is the Attenuation Law for light photons in matter (the non-differential form). It is also called the Lambert Law of Absorption, in honour of the Swiss-German astronomer/mathematician/physicist Johann Heinrich Lambert.
In actual fact m is itself a function of the photon energy, and also the material itself (its density and its composition), which means that the exponential law only applies in the case of a photon beam consisting of photons with the same energy value, in a material that is uniform in nature. Because it varies between systems (beams of different photon energy and different materials), the quantity m is called a coefficient, and is known specifically in radiation physics as the linear attenuation coefficient.
Chances of Surviving
Let's consider some of the features of what we have ended up with so far.
We have a mathematical solution telling us the number of photons per second we expect to measure at any distance, x, into material (given pre-knowledge of the number of photons per second entering the material, and also the value of the linear attenuation coefficient).
Taking the solution and dividing both sides by n0, we get
We can interpret this as "if we throw in n0 photons (in one second), then the expected fraction that survives (has not interacted with a molecule) to a depth of x is n/n0".
It is then a natural step to apply this value of the expected fraction (out of the whole bunch of photons) to the chance of any single photon surviving (as is done all the time in statistics). In this case we could assert that the chance of a single photon surviving to at least a depth x is equal to n/n0.
Notice how we have a law here that essentially reflects what must be a chance (or stochastic) process. In actual fact (but from more fundamental considerations) there is no way of predicting whether any individual photon will interact or not, only the probability of it interacting (or surviving) as a function of the depth.
So the probability a photon survives to at least a depth x is P(x) = e-mx.
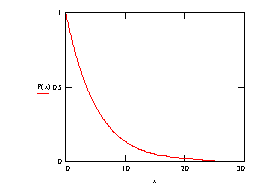
Note that the P(x) plot never drops to zero (except at a depth of infinity!) and that the rate of change of the probability of survival (the slope dP/dx) increases with distance (ie the negative slope gradually tends to "flatten"). It is interesting to consider this from a physical viewpoint.
Looking down an arbitrary line of sight of travel along which an individual photon could travel, then typically a molecule will be seen head on, as it were, and this molecule would be at some particular depth. Assuming a random collection of molecules within the material, it is of course not a certainty that a molecule will be seen head on for any arbitrarily chosen line of sight, but as the depth increases there is more and more chance that such a molecule will arise. As the depth increasese further, there is also more and more likelihood that another molecule will be encountered that "lies in the shadow" of the first molecule. Increasing the depth brings with it more "shadowed molecules" but these represent no increase in probability of an interaction for any photon that did happen to traverse that particular line of sight, since such photons have already been removed from the beam by the first head on collision.
Choosing many such lines of sight - according to a large population of photons - gives now a more general result: increasing the depth means more likelihood of shadowing, for the average photon, and so there is less proportionate increase in a chance of being absorbed, per unit depth of travel.
In The Ubiquitous Exponential Laws II - Radioactive Decay, to appear in the next issue of Plus, Ian Garbett shows how radioactive decay obeys an exponential law, and explains how we can use this fact to date artefacts such as the Dead Sea Scrolls.
About the author
 Ian Garbett lectures in applied radiation/radiological physics within the Medical Radiation Science courses at Charles Sturt University, Wagga Wagga NSWAustralia.
Ian Garbett lectures in applied radiation/radiological physics within the Medical Radiation Science courses at Charles Sturt University, Wagga Wagga NSWAustralia.
He graduated in 1977 with a BSc Honours in Applied Physics from the University of Lancaster, and obtained an MSc in Medical Physics from the University of Leeds in 1987.
He is interested in various theoretical aspects of radiation and radiological physics, with an interest in mathematical modelling in general.
Current research involves a theoretical description of X-ray beam spectra.
Comments
Anonymous
Thank you for your excellent explanation of exponential decay (attenuation) of light. This is exactly what I needed for my class of biology students.
Lore Ayoub
Anonymous
This was a tremedous article and I used it to introduce modelling with differential equations to my Further Maths group.
Thank you!
k
sum
Thanks a lot for the great article! I enjoyed it very much.
However, I just have a small problem in understanding the following statement in the Light Attenuation section: 'If a quantity is proportional to two different quantities independently, then it is also proportional to the product of those two quantities.' Isn't it that the square of the quantity, rather than the quantity itself, should be proportional to the product of the two quantities ?
Could you please clarify this ?
Marianne
Yes you are right, the sentence is wrong! Thanks very much for pointing this out. We have changed the passage accordingly and hope it all makes sense now!
Anonymous
The original is , I believe correct.
For exammple wages ...assume due to (i) rate of pay , r, Ii) hours worked. t.
So W propto r. And W propto t
Then for this simple case infact consta nt of proportion = 1
W propto r*t
W = r*t
Triple the rate of pay, double the hours worked, then W is now six times larger!
It is. Correct to then state if W propto r And, independently, that W propto t, that also W propto r*t
It would not be correct to state W^2 propto r*t. .
The original author statement is then correct.
Anonymous
Thanks for helping me understand this, where dozens of websites have failed. This will be of great help in my Physics coursework
Jay C
Wow its usually not so easy for me to grasp texts involving science or math. However, the wording and breakdown presented in your articles allowed me to comprehend the laws and reasons behind the topic. You should really consider writing textbooks or manuals to help the academic success of highschool and college students your resources are very impactful thank you Ian!! Please share more of your resources if any are available!
Sairam K
Well , I had a little idea on this topic before, but now it made me clear of what goes behind the exponential attenuation of light during absorption. Thanks for such good explanation in such a lucid language.