
The music of the primes
Many people have commented over the ages on the similarities between mathematics and music. Leibniz once said that "music is the pleasure the human mind experiences from counting without being aware that it is counting". But the similarity is more than mere numerical. The aesthetics of a musical composition have much in common with the best pieces of mathematics, where themes are established, then mutate and interweave until we find ourselves transformed at the end of the piece to a new place. Just as we listen to a piece of music over and over, finding resonances we missed on first listening, mathematicians often get the same pleasure in rereading proofs, noticing the subtle nuances that make the piece hang together so effortlessly.

The one advantage that music has over mathematics is the physical connection that our body has with the sound of a composition. The hairs on the back of my neck never fail to stand on end when I hear Schubert's Death and the Maiden Quartet. The tingle factor stimulated by some pieces of music is something mathematics is rarely able to match. This is why those without any musical training can respond to a concert performance, whereas only after years of mathematical training does one eventually have the ears to listen to the great mathematical compositions.
Listen to Schubert's Death and the Maiden
It is one of the failings of our mathematical education that few even realise that there is such wonderful mathematical music out there for them to experience beyond schoolroom arithmetic. In school we spend our time learning the scales and time signatures of this music, without knowing what joys await us if we can master these technical exercises. Very few would have the patience to learn the piano if they were denied the pleasure of hearing Rachmaninov.
Riemann's Symphony
One of the great symphonic works of mathematics is the Riemann Hypothesis - humankind's attempt to understand the mysteries of the primes. Each generation has brought its own cultural influences to bear on its understanding of the primes. The themes twist and modulate as we try to master these wild numbers. But this is an unfinished symphony. We still await the mathematician who can add the final chords to this grand opus.But it isn't just aesthetic similarities that are shared by mathematics and music. Riemann discovered that the physics of music was the key to unlocking the secrets of the primes. He discovered a mysterious harmonic structure that would explain how Gauss's prime number dice actually landed when Nature chose the primes.
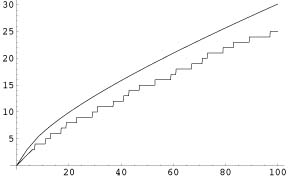
Gauss's function compared to the true number of primes
Riemann was very shy as a schoolchild and preferred to hide in his headmaster's library reading maths books rather than playing outside with his classmates. It was while reading one of these books that Riemann first learnt about Gauss's guess for the number of primes one should encounter as one counts higher and higher. Based on the idea of the prime number dice, Gauss had produced a function, called the logarithmic integral, which seemed to give a very good estimate for the number of primes. The graph to the left shows Gauss's function compared to the true number of primes amongst the first 100 numbers.
Gauss's guess was based on throwing a dice with one side marked "prime" and the others all blank. The number of sides on the dice increases as we test larger numbers and Gauss discovered that the logarithm function could tell him the number of sides needed. For example, to test primes around 1,000 requires a six-sided dice. To make his guess at the number of primes, Gauss assumed that a six-sided dice would land exactly one in six times on the prime side. But of course it is very unlikely that a dice thrown 6,000 times will land exactly 1,000 times on the prime side. A fair dice is allowed to over- or under-estimate this score. But was there any way to understand how to get from Gauss's theoretical guess to the way the prime number dice had really landed? Aged 33, Riemann, now working in Göttingen, discovered that music could explain how to change Gauss's graph into the staircase graph that really counted the primes.
Shapes and sounds
The key to understanding Riemann's ideas is to explore why a tuning fork, a violin and a clarinet sound very different, even when they are all playing an A, say. The graph of the sound wave of the tuning fork looks like a perfect sine wave. In contrast, the sound of the violin playing the same note looks like the teeth on a saw, a much more jagged sound. The animation below shows the contrasting wave shapes of a tuning fork, violin and a clarinet as they play an A.
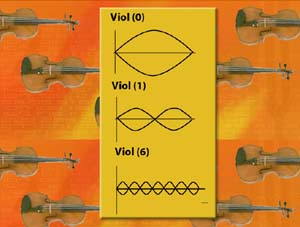
The reason the violin doesn't look and sound like the tuning fork is that it is playing, not just an A, but also a combination of different frequencies called the harmonics. We get an additional note for each sine wave that fits exactly along the length of the string. Each additional note beats faster, which means it sounds higher. As the notes get higher they get gradually quieter, which is equivalent to the height of the sine wave getting smaller.
By adding the heights of these additional harmonics onto the graph of the tuning fork, we see how we can change the sine wave into the saw-tooth shape of the sound of the violin. Follow this link to see the way the first five harmonics combine to build up the wave shape created by a violin.
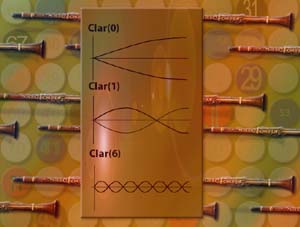
The sound of the clarinet, in contrast, is depicted by a sound wave that looks like the crenellations on a castle, which leads to its more closed sound, compared to the sharp note of the violin. In the same way as the violin's characteristic sound is made up of additional harmonic notes, the sound of clarinet too is built by simultaneously playing a combination of sine waves of different frequencies. This time the sine waves must fit the length of the clarinet but be open at one end, closed at the other. This results in the clarinet choosing a different sequence of harmonic notes to those favoured by the violin.
Again by adding the heights of all these sine waves together we can see the square shape of the clarinet emerging from the basic sine wave corresponding to the A of the tuning fork. Follow this link to see the way the first five harmonics combine to build up the wave shape created by a clarinet.
Riemann's harmonics
What Riemann discovered was that Gauss's graph is like the fundamental note played by an instrument, but that there are special harmonic waves that, when added to this graph, gradually change it into the true graph or "sound" of the primes, just as the harmonics of the clarinet change the sine wave into the square wave.

Some of the first few harmonics discovered by Riemann
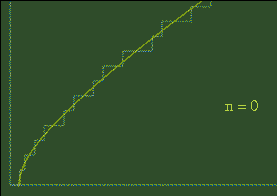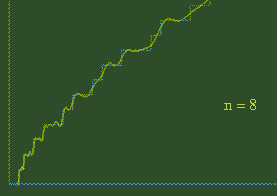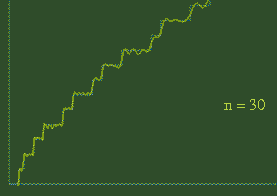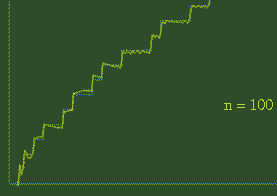
The effect of Riemann's harmonics
To the right is an animation showing the effect of adding on the first 100 harmonics. Adding on each new wave contorts the smooth graph that little bit more. Riemann realised that by the time you added on the infinitely many waves he had discovered, the resulting graph would be an exact match for the prime number staircase.
Revolutionary imaginings
But where on earth had Riemann found these strange prime number harmonics which corrected Gauss's guess into the true sound of the primes? Well, he was actually messing about with an exciting new subject that was emerging out of the French Revolution: the new world of imaginary numbers. For years people could not accept that a negative number might have a square root - after all, a negative times a negative is always positive. But the French revolution gave mathematicians the courage to think of new ideas. They invented new months and new days of the week, so why not new numbers? So came about the birth of the new number i, the square root of minus one. All the other imaginary numbers were got by taking combinations of this new number with the ordinary numbers, for example -3+4i.
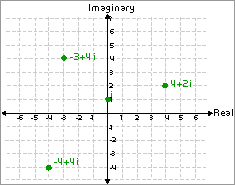
A home for the imaginary numbers
The most unsettling thing about these new numbers was working out where they were. There wasn't any room on the number line, which contained places for numbers like 2, -3, pi or e. It was Gauss, Riemann's teacher, who suggested creating a new direction for this new imaginary number i. The ordinary numbers (or real numbers as mathematicians call them) sat on the number line running East-West in this map of imaginary numbers, while the North-South direction corresponded to the imaginary part. So each imaginary number, like -3+4i, just became a point in this map: go 3 units west and 4 units north. Suddenly a two-dimensional map of the world of imaginary numbers emerged, making these numbers far more tangible.
Riemann was particularly interested in feeding imaginary numbers into functions. Usually we can draw a graph of a function where the input runs along the horizontal and the output is the height of the graph. But a graph of an imaginary function consists of a landscape where the output is represented by the height above any point in the world of imaginary numbers.

An imaginary landscape
Riemann had found one very special imaginary landscape, generated by something called the zeta function, which he discovered held the secret to prime numbers. In particular, the points at sea-level in the landscape could be used to produce these special harmonic waves which changed Gauss's graph into the genuine staircase of the primes. Riemann used the coordinates of each point at sea-level to create one of the prime number harmonics. The frequency of each harmonic was determined by how far north the corresponding point at sea-level was, and how loud each harmonic sounded was determined by the east-west frequency.
A pattern emerges
The points at sea-level could have been scattered randomly around Riemann's map. But when he plotted some of these points, a remarkable pattern emerged. The points at sea-level were all lined up: the east-west coordinate was the same for every point. This meant all the harmonics were playing in perfect balance. As the music evolved, each harmonic would crescendo but no harmonic would crescendo any louder than another. If there was a point at sea-level off this line, it would imply that one of these harmonics would eventually drown out all the rest. It would be like listening to an orchestra and hearing the sound of the tuba gradually drowning out the sound of the rest of the orchestra.
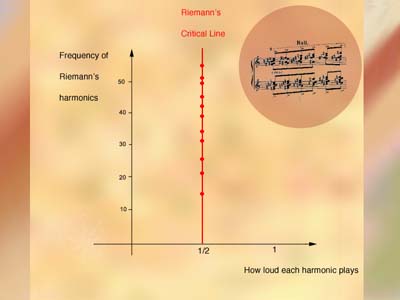
But Riemann couldn't prove that every point at sea level really lay on this magic leyline (or "critical line", as mathematicians call it) that seemed to be running through his landscape. But he hypothesised they did. And this is what all mathematicians would sell their souls to prove - even without the million dollar prize that has been offered for a solution. The Riemann Hypothesis: Prove that every zero of the zeta function lies on the line with real part equal to 1/2.
In some sense, Riemann's discovery represents a real triumph of the pattern searcher over the chaos Nature throws at us. Through Riemann's imaginary looking-glass world, the randomness of the primes is transformed into the order of these points at sea-level. Many great mathematicians have battled to prove this hypothesis and you can read their stories in my book The Music of the Primes, reviewed in issue 26 of Plus.
If the Riemann Hypothesis is true, it explains why there are no strong patterns in the primes. A zero off Riemann's critical line would cause a strong pattern to be stamped on the primes, as this one harmonic dominated the rest of the harmonics. The Riemann Hypothesis says that we believe this is not the case. The harmonics are in some perfect balance, creating the endless ebb and flow of the primes.
Gauss's guess is like the prediction that a six-sided dice thrown 6,000 times lands exactly 1,000 times on the prime side. The heights of Riemann's harmonic waves tell us how far Gauss's guess is from the way the prime number dice really landed, that is, the errors between Gauss's guess and the true number of primes.
So how fair are the prime number dice? Mathematicians call a dice "fair" if the difference between the theoretical behaviour of the dice and the actual behaviour after N tosses is within the region of the square root of N. The heights of Riemann's harmonics are given by the east-west coordinate of the corresponding point at sea-level. If the east-west coordinate is c then the height of the wave grows like Nc. This means the contribution from this harmonic to the error between Gauss's guess and the real number of primes will be Nc. So if the Riemann Hypothesis is correct and c is always 1/2, the error will always be N1/2 (which is just another way of writing the square root of N). If true, the Riemann Hypothesis means that Nature's prime number dice are fair, never straying more than the square root of N from Gauss's theoretical prime number dice.

Riemann: we still don't know if he was right
Riemann died shortly after he made his great conjecture aged only 39. Faced with the mess he left behind, his housekeeper destroyed many of his unpublished scribblings before she was stopped by members of the faculty in Göttingen. Did Riemann have a proof that was lost for eternity in the kitchen fire of his over-zealous housekeeper? We shall never know.
Riemann's early death deprived mathematics of one of the giants of its subject. Just as the world was denied the music of a mature Schubert who died at the same age as Riemann, the world is still waiting for a successor to capitalise on the insights generated by Riemann in his attempts to capture the music of the primes.
About the author

Professor Marcus du Sautoy is an Arsenal fan. His favourite primes are featured on the cover of his book The music of the primes (reviewed in issue 26 of Plus).
Comments
Anonymous
Really a question: Could someone tell me precisely what the ordinate and abscissa are in the three graphs shown? I have and have twice read "The Music of the Primes. Wonderful book, but I want more! I've got Edwards book; it's slow going, though so far I'm making it. I'm quite familiar with Fourier Analysis as applied to engineering and physics, but not to Number Theory. I have a Ph.D. in Applied Math, and am now retired and having fun studying the primes.
Anonymous
How can one compute the harmonics shown in the first picture in the section titled "Riemann's Harmonics"? Some Mathematica code would be highly preferred. Please get in touch with me at tvogler@me.com - thank you very much.
Ben
My vision isn't up to reading paper books any longer. Fonts are just too small. I went to Amazon's Kindle store to buy this, but to my regret, could not find it.
Juanmf@gmail.com
Thanks for this article, very well explained (still don't get 100% about Z function's meaning).
What's the real challenge?
A) to prove that all roots of Z fall in Real = 1/2, or
B) to prove that there exist an infinite set of harmonics, each containing the previous ones, that contains all the primes, the bigger the harmonic lenght, the bigger the accuracy?
Please contact me at juanmf@gmail.com (this commenting engine does not allow for notifications, it seems)
Edward Loper
What is the true nature of this question regarding Riemann's Hypothesis. To solve the hypothesis? To know 100% how to find and determine a prime..... And fast? Or is it in relation to space time as suggested by Tesla's believed link to singularities? What are you really looking for? Answer me honestly and without a standardised response and perhaps we can talk further. Rev.e.loper@gmail.com