Sir Walter Raleigh is perhaps best known for laying down his cloak in the mud for Queen Elizabeth I (though sadly this act of chivalry is probably a myth!) However, he also started a mathematical quest which to this day remains unsolved.

Sir Walter posed a simple question to his mathematical assistant, Thomas Harriot. How can I calculate the number of cannon balls in a stack? Harriot solved this problem without difficulty but started to wonder about a more general problem. What arrangement of the balls takes up the least space?

Harriot wrote about the problem to his colleague Johannes Kepler, best known for his work on planetary orbits. Kepler experimented with the problem and concluded that an arrangement known as the face centred cubic packing, a pattern favoured by fruit sellers, could not be bettered. This statement has become known as "Kepler's conjecture" or simply the sphere packing problem.

Fruit stacked using the face centred cubic packing.

To measure how good an arrangement is, mathematicians imagine that all of space is filled with spheres. They calculate the proportion of this infinite space, or volume, occupied by the spheres themselves. The remainder of the volume or space is formed by the gaps between the spheres.

The sphere packing problem has various applications. Firstly, it extends quite simply into other dimensions (in two dimensions it becomes the circle packing problem). It is also analogous to the problem of constructing optimal codes (see "Coding theory: the first 50 years" elsewhere in this issue). A proof of the conjecture may also help physicists to understand the structure of crystals, something that Harriot himself urged Kepler to consider in his work on optics.

Although the sphere packing problem has frustrated mathematicians for nearly four centuries there is light at the end of the tunnel. In 1953 the Hungarian, László Fejes-Tóth showed that given sufficient computing power the problem could be solved. The American mathematician, Thomas Hales is currently trying to do just that and is hopeful that within "a year or two" he will complete the calculations.

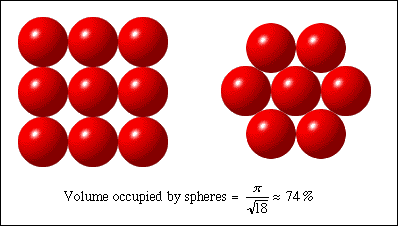
The face centred cubic packing (left) consists of layers of spheres. Each layer is positioned so that the spheres rest on the 'holes' of the layer below. This arrangement is not unique, the hexagonal close packing (right) is constructed in a similar way and is equally efficient.

The trouble with Hales' solution is that it cuts right to the heart of what many believe a mathematical proof should be. If Hales is successful there may be a feeling of anti-climax with no new insight immediately apparent.

It is therefore not surprising that some people are convinced that a more traditional proof is possible. Wu-Yi Hsiang, from California published just such a proof in 1990 but after much deliberation, the majority of mathematicians in the field remain sceptical claiming that there are holes in his argument.

Whether the holes in Hsiang's proof will be filled before Hales finishes his computation remains to be seen but it seems likely that Kepler's conjecture will, at least for the time being, remain a mathematical mystery.