
ART+MATH=X
Carla Farsi straddles two fields that many people believe are diametrically opposed: as well as being a professor of mathematics at the University of Colorado at Boulder, she is a working, exhibiting artist. After years of pursuing both interests separately she declared 2005 her Special Year for Art and Maths, and in an impressive effort put on various exhibitions, classes, movies, lectures, concerts, plays and an international conference — all to deepen the understanding of the relationship between maths and art. Plus interviewed her to find out just what this relationship is about, and what it feels like to have a foot in both worlds.

The birth of Hiroshima, Carla Farsi, oil on canvas. Reproduced with kind permission of the artist.
Painting by numbers?
When you look at some of Carla's artwork, you might be forgiven not to recognise any maths in it. Some of her installations in particular appear impulsive, even disordered, and — made from recycled objects — belong very much to the realm of reality. There are no meticulously worked out geometrical patterns, intricate fractals or perfectly recreated perspectives, as you might expect from an artist-mathematician. So what makes the connection between maths and art? Is there more to it than the fact that maths underlies patterns and perspective? "Visualisation is one of the main points," Carla says, "especially in geometry you can prove things visually, and the pictures can say as much as the actual theorem. But you can even go beyond geometry. Something that is logical, that makes a mathematical theorem, also makes some kind of a visual statement about structure and composition. It's almost like a piece of art, it has its own structure, logic, meaning. In a mathematician's head, the mathematical ideas, even if they're very abstract, can appear to be almost visual, intuitive."
Carla thinks that with the advance of computers, the visual and artistic aspects of maths will become more and more prominent: "Computers are developing so fast and we don't really know yet what they could do for us in the future. Maybe one day it will be sufficient to think about the images involved in a mathematical idea or proof, and a computer will compute the underlying equations for us. Right now, just drawing a picture is often not enough — a proper proof has to be more rigorous than that. But computers are already being used to prove theorems [see Plus article Welcome to the maths lab], and maybe one day a mathematician could simply present the computer with a picture, and the computer will be able to 'read off' the maths in it. In this way, mathematicians could spend more time on the creative aspects of maths — having the ideas — and computers could do the boring, automatic parts. At that point maths may be closer to art than it appears now."

A view of Carla's Cosmic orbifolds installation. Reproduced with kind permission of the artist.
So, what does it feel like, being an artist and a mathematician at the same time? Does proving a theorem feel very different from creating a piece of art? "No, the two don't feel very different. Of course, when you're doing maths, you're bound by rules much more than when you're doing art. In art you can change the rules — what you initially planned to do — half-way through, and I do that a lot. In fact, even if I've made up some rules at the beginning, I often find that I'm unable to stick to them, the practicalities involved force me to seek other routes."
Do Carla's motivation for doing maths and her inspiration to do art come from the same place? "Yes, I certainly think so, I'm absolutely positive about that. There is the same kind of fascination for me in both maths and art. It's all about expressing ideas, and sometimes maths works better and other times it's art.
What are these ideas? "That's a very difficult question! I think it's how I relate to the world, how I see and understand the world. I feel a relationship with certain objects, or objects of the mind, and I want to express that. For example, I may be touched by the idea of an explosion [Carla indeed painted a series of pictures on the subject of Hiroshima], and to express it, I may prefer to use art, bright colours. If I want to express or understand something more formal, maths may be better-suited."

Carla Farsi, Coming together, oil on canvas. Reproduced with kind permission of the artist.
Numbers by painting
But Carla didn't put on her Special Year just in order to contemplate those deep connections. First and foremost, she wants to open up the world of maths to those who are scared of it, or feel that it has nothing to do with real life. "Emphasising the visual and creative aspects of maths might make people like it more. I created a course at my university, aimed at non-maths students, which teaches maths using the visual arts. I think this could also be of great benefit to maths students, and here we could teach the more formal mathematical ideas."
A detail of a Gaudí mosaic.
Carla uses paintings and sculptures both to give an overall feel for the subject and to illustrate concrete maths objects and problems. An area that benefits most from the visual approach is topology. This branch of maths studies the nature of geometric objects by allowing them to distort and change. Think of a knot in an elastic band: its defining feature, the way the band winds around itself, remains the same even when you stretch the band. In this spirit, topologists regard any two objects that can be deformed into each other without tearing to be one and the same thing — have a look at Plus article In space, do all roads lead home? to see how a coffee cup can be turned into a doughnut.
Carla teaches topological ideas and methods using the sculptures of North American artist Helaman Ferguson, and also the works of Catalan architect Antoni Gaudí.
"With Gaudí I am a bit more loose. I introduce him when I talk about topological transformations of surfaces and also when I talk about spirals. Some of his work illustrates well the concept of topological deformation and I use it for that, as a general example. This is also useful when students ask (as they often do) how mathematics relates to things they see in the real world."

Detail of Gaudí's Casa Battló
Of course, no class on maths and the visual arts would be complete without fractals. Their often astonishing beauty comes from their infinite intricacy: no matter how closely you zoom in on a fractal, what you see is still extremely complicated and crinkly. What's more, it often looks similar to the whole fractal, a phenomenon called "self-similarity" (see the box on the Von Koch Snowflake below). There are various mathematical techniques to measure the crinkliness of a fractal, and Carla teaches them in her classes with the aid of fractals that occur in nature and art: "I teach my students how to compute the fractal dimension of a fractal. First I show them some examples from art and other fields, especially nature. Then we study the technique formally, and then apply it to images of fractal art. We also work out the fractal dimension of some of the original examples I presented them with."
As Carla points out, there are paintings containing fractals that were never consciously intended by the artist: mathematicians have shown that the drip paintings by abstract expressionist Jackson Pollock can be identified by their own particular fractal structures (see Plus article Fractal expressionism).
Symmetry is another concept that is as visual as it is mathematical. We can perceive it almost subconsciously — and it has been argued that it plays a vital role in our perception of beauty — yet it opens the door to a wealth of mathematical structure. A square, for example, has 8 symmetries: you can reflect it in the vertical, horizontal or diagonal axes, you can rotate it through 90, 180 or 270 degrees, or you can simply do nothing and leave it as it is. Each of these transformations is called a symmetry, because after you've done it, the square appears to be exactly as it was before. If you put all these 8 symmetries together, you get a self-contained system: whenever you combine two of them, by first doing one and then the other, you get one of the other symmetries in your set — try it! Such a self-contained system of symmetries is called a group, and symmetry groups are the gateway to abstract algebra. A simple visual consideration lands you in the thick of some quite advanced mathematics!
The Von Koch Snowflake The Von Koch snowflake is a fractal which is constructed from an equilateral triangle as follows: 1) remove the middle third of each side, If you keep going indefinitely, you end up with the fractal shown on the right. The outline of the snowflake is incredibly crinkly. In fact, it does not contain any straight line pieces at all: the middle third of any piece of straight line has been replaced by two sides of a triangle, creating a spike. Mathematicians measure the crinkliness of a fractal by the fractal dimension, a generalisation of our ordinary notion of dimension. The outline of our snowflake is too crinkly to be one-dimensional. On the other hand, it clearly is not two-dimensional either, since it contains no area. In this case, the dimension lies between 1 and 2, in fact it is equal to log(4)/log(3) = 1.2619. |
So, clearly, the visual arts can provide a very good entry to maths for non-mathematicians, but how would mathematicians or maths students benefit from a visual arts course? "It would help them to improve their visual skills," Carla says, "and this helps with mathematical intuition. I remember when I did my PhD, the professor would sometimes sketch something on the board to aid understanding, but those sketches usually got discarded pretty quickly. I think that, especially with the help of computers, people could learn how to "see" things they previously found hard to imagine. Colours, for example, can be used to convey a lot of information. Textbooks often only contain black-and-white pictures, if any. I think that someone skilled in the use of colours could create diagrams that represent the ideas much better". This is indeed something that has been done in some areas of mathematics. The famous Mandelbrot set, for example, is so colourful not only because it is prettier that way. The colours also have an exact mathematical meaning.

A detail of the Mandelbrot set.
Carla thinks that it is time to rethink the way we teach maths. "I can only really speak about my own school experiences in my native Italy, but I think that mathematics is often taught in a way that focuses more on the formal language than on ideas. I think there are many maths teachers who are not too aware of the ideas behind the maths and simply teach equations and formulae. So people usually don't see maths as a creative subject. Also, mathematics is hard, and if people find it difficult and not creative — well, of course they won't like it! We should think very hard about education and try to focus on ideas, rather than technicalities. Again, computers and visual representation could be pivotal in this. That's why I set up the Special Year; I really wanted to make people aware of what doing maths is really like, and that it has creative aspects."
The Special Year for art and maths
The range of activities Carla put on during that year is truly impressive. You can admire some of the visual exhibits on the digital gallery. In some of the works the connection to maths is clear: there is a beautiful digital rendering of some fluid-mechanics equations by Mark Stock, a self portrait depicting the "eureka moment" by Harvey Goldman, and an intricately patterned woven quilt by Erin Russek.

Sri Yantra, Erin Russek, fabric. Reproduced with kind permission of the artist.
Other exhibits, however, are not so clearly connected to maths. Sarawut Chutiwongpeti's video installation Untitled (Wishes, Lies and Dreams) explores the mechanisms underlying perception and the world of dreams and the unconscious. Does the unconscious play a part in maths, too? "I'm sure it does," Carla says, "though it's hard to express how exactly; I'm not a psychologist. It's the place from where we all bring our ideas. I think there is a connection between dreams and maths. Dreams have their own logic, that doesn't immediately make sense. In mathematics, too, we use many different types of logic, sometimes counterintuitive ones.

Droplet #7, Mark Stock, digital art. Reproduced with kind permission of the artist.
The exhibitions of visual art form only one aspect of the Special Year. There are various plays and concerts, each stressing that maths — and mathematicians — do not exist in an isolated world of books and blackboards. An example is Hugh Whitemore's play Breaking the code, directed by Cecilia Pang. It describes the life of Alan Turing, whose mathematical genius helped to break the Germans' Enigma code during the Second World War, but whose homosexuality meant that he was also breaking the moral code of the time. He was tried and punished for what the authorities considered his crime, and ultimately committed suicide. Carla says: "This piece is a magnificent illustration of an important concept: that mathematics and mathematicians are an integral part of the history of their time and not a totally isolated community, removed from the 'outside world'. Turing isn't an exception; there are many mathematicians whose non-mathematical lives influence their work, for example many women. But I believe that the relationship between maths and society is still more complex than this. The maths a society develops reflects its values and expectations — the maths the Maya did is different from that of the ancient Greeks."

O, Harvey Goldman, digital art. Reproduced with the kind permission of the artist.
A concert called Mathematics made music was another highlight. Most pieces — all performed by A. May, though written by different artists — used computers to generate or distort sound. An example is Brian Evans' Amazilia. Evans digitalises sound — he turns it into numbers — which then get mapped to coloured points on a screen, and to new sounds. The result is a piece that slowly unfolds in front of your eyes and ears.
What is Carla's favourite aspect of her Special Year? "There is so much, it's hard to tell. What I found extremely rewarding is the way people reacted to it, especially people who are not mathematicians. They were very enthusiastic; I was only able to organise the program because I had so many volunteers helping me. People liked the idea that someone from the maths world was trying to engage the general public by representing maths in a way they could understand, and by introducing art that has mathematical meaning." And were mathematicians equally enthusiastic? "I found a good number of people who were interested, but also some that weren't, though they were a minority." What were their objections? "I think some people felt that by combining maths and art you lose some of the precision of maths, and some of the mathematical content — which is true, of course. I think some professional mathematicians find a lot of comfort in the rigour and structure of maths, and are reluctant to let that go."

A scene from the play 'breaking the code'.
Folding the orbit
Finally, let's have a look at a piece of Carla's own work: an installation called Cosmic Orbifolds (depicted above), which directly represents a maths object. Orbifolds come out of the study of groups, like the symmetry groups described earlier. This time, rather than a square, think of a round disk, and imagine rotating it around its centre; clockwise through 90 degrees. If you do this twice, you get a rotation through 180 degrees, three times gives a rotation through 270 degrees, and four times gets you back to where you started. As before, these rotations together form a group. Mathematicians say that this group "acts on the disk".
But what does it do to the disk? Well, it cuts it up into four equal pieces; see figure 1. Each rotation moves a piece to one of the other three pieces. In a sense, the four pieces are equivalent; the rotations simply interchange them. Once you know something about one piece, for example its area, you automatically know the same about the other three pieces. So, really, once you've got the rotations, it's enough to just consider one quarter of the disk. What's more, the radial segment a, which forms part of the boundary of the quarter piece, gets moves by a rotation to the radial segment b, which is part of the same quarter piece. In terms of our rotations, the two segments a and b are equivalent, so we glue them together and get a cone.
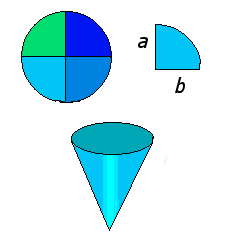
Figure 1
This cone is what mathematicians call the orbifold of the group. It encodes all the information about the group and the way it acts on the disk. We can reassemble the disk simply by cutting open the cone and applying our rotations to the resulting quarter. The point at the tip of the orbifold is special: it corresponds to the centre of the disk and is the only point that gets moved nowhere by the rotations. It's called the singular point of the orbifold.
Carla has worked a lot with orbifolds in her PhD thesis, which was about something called "C-star algebras". The orbifolds she worked on are spheres, not cones, but they also have singular points. "I found that the spheres were best represented by tents — especially since I don't have large amounts of money or tools to create spheres out of any other material. I like working with recycled objects a lot, it's very rewarding." The singular points are represented by umbrellas stuck into the tents. As in our example above, these singular points come from groups of rotations, and the segments of the umbrellas hint at that: each triangular umbrella segment can be moved to another by a rotation. "The idea was to represent all the orbifolds you can get from certain groups acting on a doughnut shaped space, or torus. But when I started putting my idea into practice, I got lost: I encountered lots of practical problems and had to change my 'rules'. But I enjoy that! In art you are subject to a 'rule of reality', while maths is so perfect. And what I like doing is to take those perfect mathematical buildings and put them into reality".
About this article

Carla Farsi is professor of mathematics at the University of Colorado at Boulder and an artist. She got her Mathematics PhD in 1989 from the University of Maryland and is the inventor and main organizer of the "2005 CU Special Year in Art and Mathematics". Her research specialty is non-commutative differential Geometry. As an artist, she likes to use recycled objects to build up humongous and chaotic geometric installations.
Marianne Freiberger is co-editor of Plus.
Comments
Anonymous
Hello there,
I have found your website very interesting to how Mathematics does relate to Art. I have set my self the dissertation question, "How can exploring the (shape and space) aspects of certain artists be used, to consolidate children’s mathematical understanding for e.g. Tessellation/ symmetry? " I have set myself this question because I am trainning to become a primary school teacher, and I am very passionate for the subjects mathematics and art, I also believe that there are clear links between both of these subjects.
I have chosen the above to be my question, as I want to see if you are able to consolidate children’s mathematical understanding by using artists’ work. Children should gain a greater understanding about the meaning of key vocabulary used in shape and space. I do believe that I will be able to consolidate children’s mathematical understanding effectively depending on the artists and their work I decide to work with.
I have been looking for some relevant literature, but I am unable to find huge amounts. Could you point me in the write direction please?
My email address is che_jay@hotmail.co.uk
Thank you
Jay Chavda
Anonymous
you probably know about this artist already but I mention him just in case
Anonymous
i really liked the way you has used maths in art.