
The trouble with five
We are all familiar with the simple ways of tiling the plane by equilateral triangles, squares, or hexagons. These are the three regular tilings: each is made up of identical copies of a regular polygon — a shape whose sides all have the same length and angles between them — and adjacent tiles share whole edges, that is, we never have part of a tile's edge overlapping part of another tile's edge.

Figure 1: The three regular tilings.
In this collection of tilings by regular polygons the number five is conspicuously absent. Why did I not mention a regular tiling by pentagons? It turns out that no such tiling can exist, and it's not too hard to see why: a regular pentagon has five interior angles of 108°. If we try to place pentagons around a point, we find that three must leave a gap — because 3 × 108 = 324, which is less than the 360° of the full circle — and four must overlap — because 4 × 108 = 432, which is more than the 360° of the circle (see figure 2).
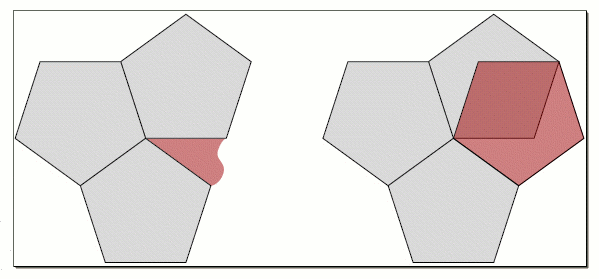
Figure 2: Three pentagons arranged around a point leave a gap, and four overlap.
But there is no reason to give up yet: we can try to find other interesting tilings of the plane involving the number five by relaxing some of the constraints on regular tilings. Let us drop the restriction that the tiles be identical copies of one polygon, and ask only that each individual tile have five-fold symmetry. That is, every tile contains a centre of rotation p such that rotations about p through 1/5th, 2/5th, 3/5th and 4/5th of the circle — in other words through multiples of 72° — leave the tile unchanged.
Is it now possible to find a set of shapes with five-fold symmetry that together will tile the plane? We refer to this question as the five-fold tiling problem. Given the rich variety of five-fold shapes available, it seems possible that we might find a tiling based on them. Though easily stated, the problem turns out to be surprisingly subtle. Although it has occupied some of the greatest thinkers of mathematical history, it is still only partially solved. The problem is also a source of many wonderful geometric designs, with more waiting to be discovered by anyone willing to experiment.
Going for simple shapes
Putting aside for now any deep mathematical reason why such a tiling should or should not exist, let us attempt to construct one a piece at a time. We'll start in figure 3 with a regular pentagon, a very simple shape possessing five-fold symmetry. We know we can attach pentagons to each of its sides, leaving five 36° gaps. We can fill these gaps by introducing pentacles (five-pointed stars) as an additional shape. The gaps left behind by the pentacles can in turn be filled with more pentagons, this time in two sizes. Now we find that there is no easy way to add another layer of shapes. Pentacles, shown in red in the top right of the figure, would overlap.

Figure 3: Constructing a tiling piece by piece.
We could introduce yet another shape, for example the one labelled with a question mark, but this new shape doesn't seem quite as innocuous as a pentacle. Furthermore, we have no reason to believe that the new shape would allow us to tile the rest of the plane; it may only buy us some time before we get stuck again. If we back up and begin with the pentacle, as in figure 4, we find that we can build a fairly large patch of tiles, including a newly-introduced regular decagon, a regular polygon with ten sides. Eventually, though, we get stuck again.
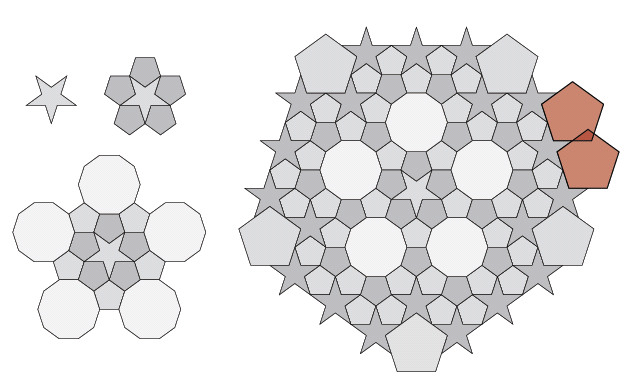
Figure 4: Starting with a pentacle — eventually you get stuck again.
Figure 5 shows that a central decagon performs poorly as well. With a bit of persistence, it is possible to show that the four shapes we've used so far (small pentagon, large pentagon, pentacle, and decagon) cannot tile the plane in any arrangement.
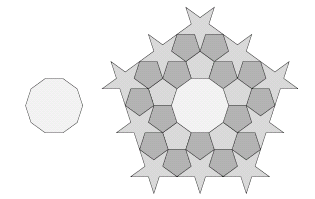
Figure 5: A central decagon performs poorly too.
The rhombus: not five but fitting
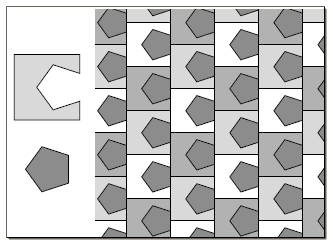
Figure 6: Take a pentagonal bite out of a square to get a tiling involving pentagons.
We might go on in this manner, inventing families of shapes and checking how large a patch of tiles we can construct with them. Another approach is to admit some additional shapes that don't have five-fold symmetry. We can then produce tilings of the whole plane more easily, and search for a way to suppress the objectionable tiles. In a way, allowing extra shapes makes the problem too easy. Any polygon known to tile the plane can have a pentagonal "bite" taken out of it, and this new shape will tile in combination with the pentagon, as seen in figure 6. We will take a more principled approach, and the elegance and ingenuity of the tilings we will encounter makes up for the ease with which we produce them.
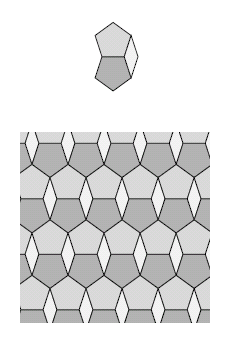
Figure 7: An octagonal region formed by a rhombus and two regular pentagons tiles the plane.
It is easy to see that two regular pentagons together with a 36° rhombus form an octagonal region that can tile the plane: you simply start with one initial tile and then keep shifting it along in a certain direction horizontally as well as diagonally upwards and downwards (see figure 7). In fact, there are infinitely many ways to tile the plane with these two shapes. Perhaps the most famous of these is the radial arrangement shown on the left of figure 8. It was described by the German artist and mathematician Albrecht Dürer in the sixteenth century, in Underweysung der Messung, a manual on painting. With the addition of a single central decagon, we can also create an attractive spiral layout, as shown on the right in the figure. As with all finite drawings of tilings, we assume the reader can imagine how to continue the patch shown to fill the whole plane.
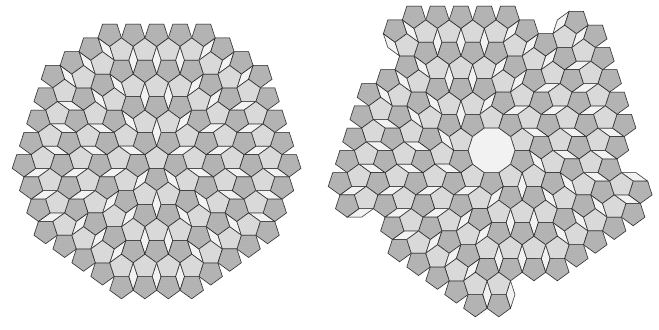
Figure 8: The radial arrangement on the left was described by Dürer. The spiral arrangement on the right incorporates a regular decagon.
Admitting monsters by substitution
Once we have allowed shapes like the rhombus which does not have five-fold symmetry, is there perhaps a way of subdividing them into more suitable shapes? This question leads us to an important concept in tiling theory — that of a substitution rule — and to another great genius — Johannes Kepler.
Given a finite patch of tiles, a substitution rule (sometimes called a deflation rule) replaces each tile in the patch with a collection of smaller tiles. One possible set of substitutions for the pentagon and rhombus are: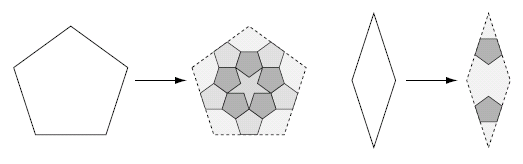
Figure 9: Each shape is replaced by a collection of smaller shapes.
The resulting periodic and radial tilings are given in figure 10. When the original patch does not have any rhombi adjacent to one another, we obtain a new tiling with four shapes: a pentagon, a pentacle (five-pointed star), a decagon, and a shape formed by fusing together two decagons.
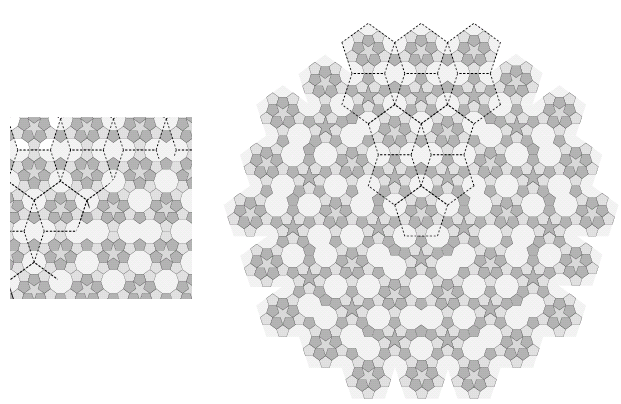
Figure 10: Tilings that result when the substitution rules of figure 9 are applied to the tiling of figure 7 and the first tiling of figure 8.
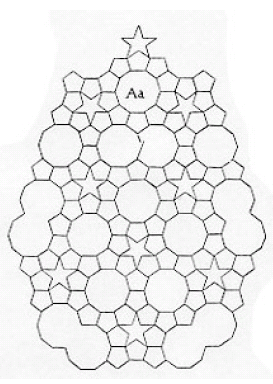
Figure 11: Kepler's drawing labelled Aa.
Applying the substitution to Dürer's radial arrangement leads to an especially interesting tiling. It can be found in Harmonice Mundi, Kepler's seventeenth century treatise on astronomy and geometry. Kepler drew several arrangements of five-fold shapes, perhaps implicitly in search of an answer to the five-fold tiling problem. The patch of tiles he called Aa, shown in figure 11, is the largest of his drawings. It uses the fused decagons, which Kepler called monsters. The text accompanying the drawing suggests that Kepler had an idea of how to extend the patch to cover the whole plane. In the twentieth century, several mathematicians showed formally how this construction may be carried out. The hidden connection demonstrated here between the drawings of Dürer and Kepler represents a pleasing bridge spanning the hundred years between these two great thinkers.
Dividing monsters forever
Our substitution certainly does not solve the five-fold tiling problem. It eliminates the rhombi of the original tiling, but introduces monsters (which have only two-fold symmetry) in their place. We can avoid adding such an odd shape to our vocabulary by subdividing every monster into pentagons, pentacles and rhombi:
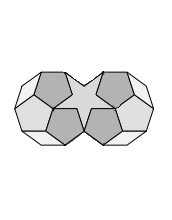
Figure 12: Dividing the monster into pentagons, pentacles and rhombi.
Since our deflation rule for the rhombus always gives rise to a monster, we can incorporate the subdivisions of rhombus and monster in a single step, as shown in figure 13 below. We can now also define substitutions for the pentacle and the decagon, giving rise to the following set of substitution rules:
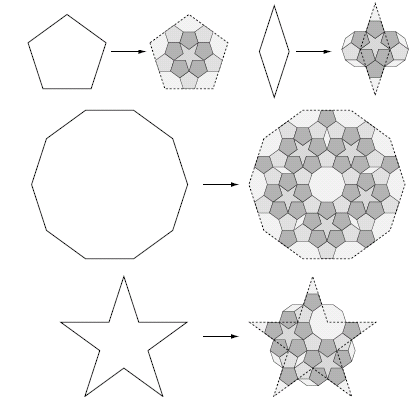
Figure 13: A complete set of deflation rules for a pentagon, pentacle, decagon, and rhombus. The substitutions for the rhombus and the pentacle do 'stick out', but this is alright, as it will not cause any inconsistencies.
These substitutions allow us to produce yet another generation of tilings:
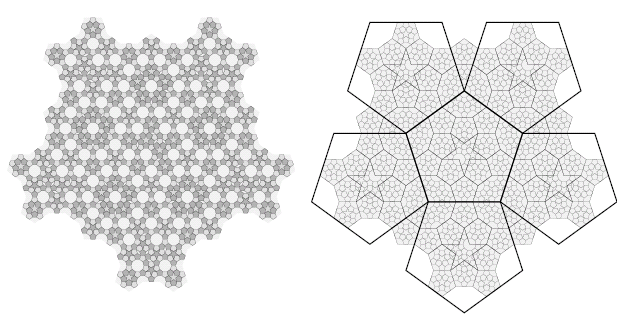
Figure 14: A small part of a tiling produced from pentagons and rhombi via two applications of the substitution rules in figure 13. The diagram on the right shows the relationships between tiles at all levels of substitution.
[If this is too small for you, look at a larger version of Figure 14.]
In fact, at this point no new tile shapes are introduced and we can go on creating an infinite sequence of tilings via substitution. Note that every generation will include rhombi; we can't solve the five-fold tiling problem simply by applying a sufficient number of substitutions. Figure 15 shows the substitution rules applied to the spiral arrangement in figure 8.
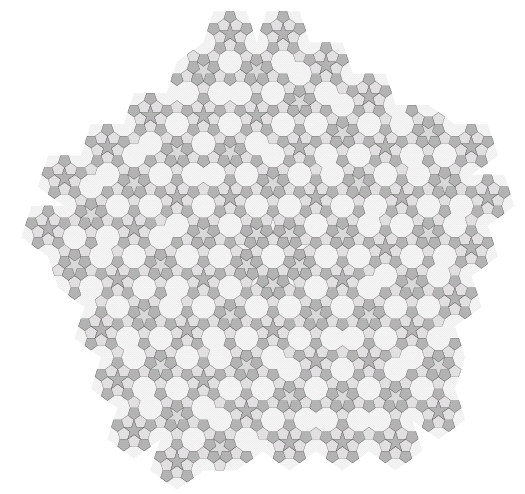
Figure 15: The spiral arrangement from figure 8, with rhombi subdivided as shown in figure 9, and the other shapes subdivided as shown in figure 13. We could suppress the monsters by subdividing them as in figure 12.
Penrose tilings
A different substitution system, also based on the regular pentagon, was devised in the twentieth century by Sir Roger Penrose, and led to an amazing new discovery. Penrose observed that a pentagon could be packed with a flower-like arrangement of six smaller pentagons, as in the first step of figure 3. The packing leaves some empty space in the original pentagon, in the form of five isosceles triangles with angles of 36° at their peaks. As demonstrated in figure 16, the same six-for-one substitution can then be applied to each of the six smaller pentagons, leaving rhombic tiles surrounded by six pentagons. In the next generation, the rhombi grow into spiky shapes. Penrose observed that the spiky rhombi can be simplified by inserting pentagons, dividing each into a pentagon, a pentacle and a half-pentacle or "paper boat". (You can read more about this substitution system in the article Pentaplexity by Roger Penrose.)
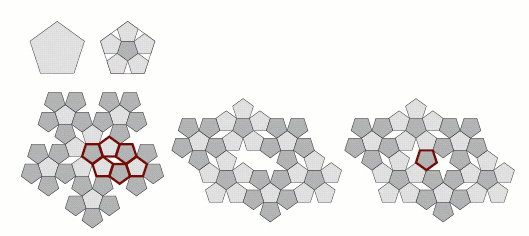
Figure 16: The first few steps in the development of Penrose's substitution system.
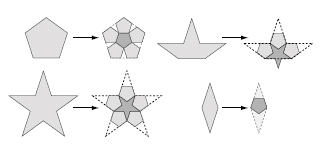
Figure 17: A full set of substitution rules.
The placement of the new pentagon suggests suitable substitution rules for the pentacle and half-pentacle as well. We arrive at a family of four shapes, together with substitution rules (shown in figure 17) that allow the shapes to be developed into tilings of the plane.
Here is an example of a patch of tiles produced using these rules:

Figure 18: A patch of tiling produced by Penrose's substitution rules.
[See a larger version of figure 18.]
The new discovery mentioned above came from a simple modification of this tiling system. By making a few simple changes to the six shapes involved, Penrose succeeded in creating aperiodic tilings. Unlike the designs we've seen so far, these tilings never repeat themselves exactly as you move along a straight line in any direction. For many years previously it had been believed that aperiodic tilings made up of only a finite number of shapes did not exist. Later and even more impressively, Penrose managed to build aperiodic tilings from only two shapes, as seen in figure 19. [Read the Plus article From quasicrystals to Kleenex to find out more about aperiodic tilings.]

Figure 19: An aperiodic Penrose tiling, based on two shapes.
From the point of view of the five-fold tiling problem, Penrose's system above seems less satisfying than our first example because it relies on two shapes that don't have five-fold symmetry: the rhombus and the half-pentacle. There are ways of eliminating the half-pentacle (see John Savard's web site for an example), but that brings us back to a system with the same single objectionable shape, the rhombus.
Pushing out the odd shapes
Is there perhaps some way to use the tilings we have developed so far to assist in solving the fivefold tiling problem? We can't simply eliminate the rhombi — it's possible to prove that the remaining shapes in our vocabulary will not tile the plane without them. They seem to act as "defects" that allow these odd five-fold shapes to fit together. However, perhaps there is a way to suppress the rhombi, or replace them by different shapes that do have five-fold symmetry.
One way of suppressing the defects would be to confine them to a bounded region in the tiling, or pepper them very sparsely among the five-fold tiles. Such a construction could lead to a limiting process: if we confine the defects to smaller and smaller regions, or make them sparser and sparser we eventually end up with the concentration of defects going to zero. A wonderful bit of tiling theory called the extension theorem says that if you can tile an arbitrarily large region of the plane with a finite set of shapes, then you can tile the whole plane with them. In other words, if I can show that no matter how large a region of the plane you give me, I can tile it with my finite collection of shapes, then this means that my shapes can tile the whole plane. As defects get sparse, we would be able to identify increasingly large regions containing only five-fold tiles. We could then apply the extension theorem to argue that the five-fold tiles should suffice for the whole plane. However, finding a way of making defects sparser and sparser is likely just as difficult as any other attempt to solve the five-fold tiling problem.
Swallowing defects
What about adding more shapes? A natural idea is to merge a defect with a few neighbouring tiles, swallowing it up inside a new tile with five-fold symmetry. In the case of our first substitution system, we can search the neighbourhood of each rhombus for the smallest collection of neighbouring tiles that can be combined this way. Sure enough, we can eliminate most rhombi by introducing two larger tiles, corresponding to pentacles and decagons at the next-to-last level of deflation. Figure 20 shows the result of this transformation applied to the patch from figure 14.
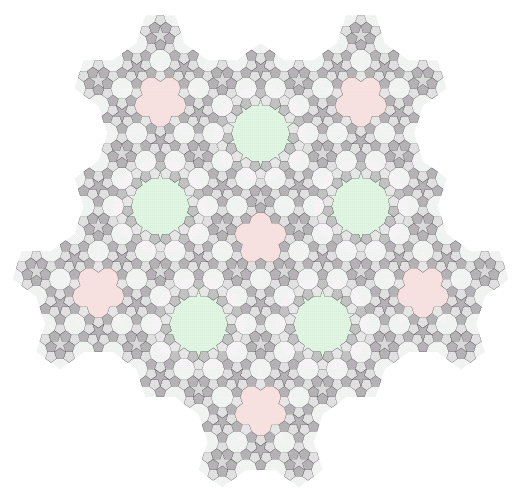
Figure 20: Swallowing up tiles in the patch from figure 14.
(You can see here how exactly this works.)
The defects are all gone, but the problem is merely deferred. It turns out that this patch cannot be made to tile the plane without re-introducing new defects. To swallow up these new defects, we will require an infinite sequence of new shapes, ever increasing in size. In theory, we might ultimately reach a stage where the newly-created large tiles can be filled with smaller ones, though the possibility seems remote.
Tiles within tiles
Still, this is a solution of a kind. If we keep swallowing up defects indefinitely, then in the limit we do obtain a tiling in which every tile has five-fold symmetry. In fact, if we are willing to allow our tiles to become infinitely large, we immediately gain access to much simpler solutions, for example the one shown in figure 21. Here, the tiling is achieved not by placing tiles alongside each other, but by nesting them inside each other: simply stick five pentagons into the corners of a pentagon three times the size. Repeat this process indefinitely and you end up with a tiling with five-fold symmetry that fills the whole plane.
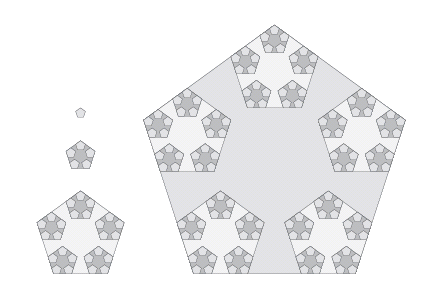
Figure 21: A very simple tiling of the plane by five-fold tiles, where the tiles are not limited in size. Every stage produces a pentagonal region, five of which nestle into the corners of a pentagon three times the size. The result is a tiling by small pentagons and 'wheels' of geometrically increasing sizes.
But in either case, the fact that we require tiles that are arbitrarily large is rather unsatisfactory. To make sure that tiles stay within a finite range, mathematicians add an additional restriction to the problem. Formally, they ask that the tiling be uniformly bounded: there should exist positive real numbers r and R such that every tile contains a disk of radius r and is itself contained in a disk of radius R. The uniformly bounded version of the five-fold tiling problem is still unsolved.
Different geometries
There are other surprising answers to the five-fold tiling problem. If we move from the flat Euclidean plane to the surface of a sphere, we find that three spherical pentagons can meet around a point with no space left over, and in fact we can tile the sphere with twelve pentagons. The tiling looks like a dodecahedron that has been inflated like a balloon:

Figure 22: Twelve pentagons tile the sphere.
Another non-flat geometry, hyperbolic geometry, even allows infinitely many ways to tile the plane by regular pentagons. [For an introduction to hyperbolic geometry and hyperbolic tilings read the Plus articles Strange geometries and Non-Euclidean geometry and Indra's pearls.] The flatness of Euclidean space seems to interfere with the ability of five-fold shapes to tile. Somehow, fiveness and flatness have a difficult time getting along together.
Like many problems in tiling theory, the five-fold tiling problem is very easy to state but far from obvious to solve. An affirmative solution would probably be straightforward to demonstrate — one simply exhibits a tiling — but would require a profound act of ingenuity to discover. However, proving that no such tiling could exist seems still more difficult. A negative answer is in effect a statement about all possible tilings, that none of them can consist entirely of five-fold shapes. It is difficult to see how we might go about furnishing a proof of this kind.
We are left therefore with a tantalising mathematical problem, and the wonderful geometric designs it inspires. And of course, there are many related questions worthy of study. Grünbaum, Shephard and Danzer, who first discussed the five-fold tiling problem, try to quantify how far one can get simply by gluing together five-fold shapes. And of course, we can pose an analogous n-fold tiling problem for every n > 6!
All such problems are unsolved. Is it easier to solve the 117-fold tiling problem than the five-fold version, or will they all fall to the same master proof? Whatever the answer, I look forward to seeing the beautiful mix of mathematics and geometric design that arises in the search.
About the author

Craig Kaplan is an assistant professor in the Computer Graphics Lab at the University of Waterloo. He is interested in the application of computer graphics to art and ornamental design, and in particular the use of geometry and tiling theory in graphics.
Comments
Anonymous
"The trouble with five" is amazing, thanks
Luis Restrepo
Anonymous
This deserves some serious attention, but the shapes are also just lovely.
Anonymous
Interesting which thinkers you mention - Kepler, Durer being most familiar - both fascinated with harmonics. Does phi enter into the dilemma of neatness with respect to pentagonal tiling?
Anonymous
phi does play an interesting rôle in Penrose tilings. Not only as the ratio of the sides of the tiles, being long/short = phi, but also as the ratios of the numbers of different tiles in any patch. And many more if you plunge into them.
Anonymous
The golden ratio is related to the square root of five. (To be exact, it's equal to half the square root of five plus a half.) Many shapes involving fivefold symmetry will have ratios of root five, and thus be related to the golden ratio in some way. If you look hard enough, you can also find phi in three-dimensional fivefold shapes, such as icosahedrons.
Anonymous
I have been busy with this too, and you may like the result:
http://www.mtenhave.net/5/index.htm
From a simple algorithm I derive lines that form pentagons. I is a never repeating system with two distances, with the golden section as ratio. It is explained on the page.
Ye
Have you made any progress recently?
Mtenhave
Hi, I am commenting on "Have you made any progress recently?". No what I am using is one (in principle infinite) string of distances. Now with the program anyone can modify the offset, layers and colors and transparency. With the offset one changes the whole pattern of pentagons. What remains is the rotational symmetry. The latest version has a very good user interface to change the colors and transparency of the layers. And if you are a bit lazy, just press "Q" and it will generate random offsets, colors and transparency, and it will store them too.
Pompilio
I purchased 50 boxes containing 6 ceramic tiles each. There are two 16" x 16" tiles, one 16" x 24" tile, two 8" x 8" and one 8" x 16". How can I create a pattern with a 1/8 inch soace between them. I have tried, but I can't figure it out. Any math specialists here? The 8" squares tiles seem to be giving me a difficult time. For example, If I put two 8 x 8 with a 1/8 space between the two beside a 16 inch tile, the joints do not join. There has got to be a pattern that works! Please help.
Macgyver 701
By leaving a 1/8" gap you will not be able to create a pattern that does not have misaligned joints. By leaving a gap between them you are essentially increasing the size of the tiles by 1/8" in each direction. Hope this helps.
Yasmine
Great post! Thank you so much, your efforts are really appreciated!
Xavier
The lower part of the subdivisions of rhombus and monster in a single step shown in "sigure" 13 features :
1 lighter pentacle & 3 darker pentagons around the same vertex...
Shouldn't there be 1 lighter pentagon "between" 2 darker pentagons (opposite to the lighter pentacle) ?
rosy.calvert@kcl.ac.uk
Great article!
I would like to play tiling with my grandchild. Aged 3 but interested in maths.
Where can I buy pentagons? Magna-tiles very expensive and few pentagons.
Don't think she has the dexterity to use paper.
Thanks