Why does a financial mathematician think about birds when trying to understand the grounding of aeroplanes after the Icelandic volcano eruption?

To understand the question, I need to explain that financial mathematicians are primarily concerned with how to make good decisions when faced with uncertainty. Now, there is a widely held view that rational people will always avoid taking a risk, yet in the financial markets there are thousands of people making money by taking the opposite course of action — are they irrational? This is a fundamental question and means that financial mathematicians need to talk to psychologists, sociologists, anthropologists, and in my case, zoologists to get the answer.

Stay put or take a risk?

I used to work in the oil industry trying to figure out how to find oil, specifically how an oil company should behave, what its strategy should be, if it was running out of oil reserves and was facing bankruptcy. My employers turned to a zoologist, Alex Kacelnik, for the answer.

Alex is an expert on bird behaviour and explained to the oil executives that their problem was very similar to the problem birds face in the winter. In a British winter some birds need to find up to 40% of their body weight in food to survive a cold night. Often birds have to make a decision: do I stay were I am, where I know there are a few berries, or do I fly off and hopefully find a new bush with a bonanza of berries? This problem gets to the heart of the research I now do as a mathematician.

Lets build a simple model. Say a bird has to find nine berries in six hours and can do this in one of two ways:

• Stay where it is with a 50:50 chance of finding one berry in an hour or finding two berries in an hour;
• Fly off to a new field, using a berry's worth of energy reserves but with a one in six chance of finding ten berries, but a five in six chance of only finding one berry, replacing the energy lost in flying. Essentially there is a 1/6 chance of a net gain of 9 berries or a 5/6 chance of a net gain of 0 berries.

Both strategies offer the same expected net gain of berries in an hour (1.5 = 1/2+2/2 = 9/6+0/6), and so the bird expects to find the nine berries it needs over the six hours.

Most people would agree that the "stay" strategy is less risky than the "fly away" strategy. So, should the bird play safe? Rather than treating this as an abstract problem, why not experiment at being the bird using a simple java applet (requires Java to be enabled in your browser, opens a new window).

What you may discover is that, if in the first four hours you have only found four berries, you are going to die if you carry on with the "rational" strategy of playing it safe, since at most you will end the day with just eight berries. The best thing to do in this case is to take the risk, since this at least gives you a chance of surviving. Similarly, if after four hours you have found eight berries, why not take the risk in the fifth hour? You may get lucky, but if not, you will get your ninth berry in the final hour by sitting pretty. The extra berries you find can be laid down as fat and put you in a good position for spring breeding.

Doing some simple maths and plotting hour versus number of berries found, we can identify three regions.

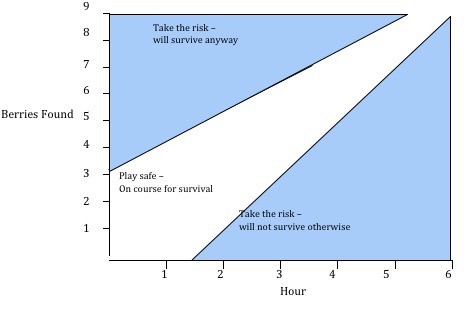
The best strategy for the bird to take depends on the state it is in — the time and number of berries found — and is not static. It's not sensible to stick either with a safe or risky strategy throughout the day and irrespective of how well you have done.

It turns out that companies, like oil companies, behave in a similar way. If you are a small struggling company facing bankruptcy you should be taking a risk, similarly if you are a big wealthy company you can afford to take a risk. However, if you are a medium sized company, your best bet is to muddle on and not take a risk, since you are as likely to fail as to succeed. The question for managers is, where, in the state space, are the boundaries between the strategies?

There is a lot of mathematical research into how decision makers, particularly in finance, should change their strategies depending on their situations. But what does our simple model tell us about flying through the ash cloud?

On 22 April, the BBC reported that the International Air Travel Association were stating that: "For an industry that lost \$9.4bn last year and was forecast to lose a further \$2.8bn in 2010, this crisis is devastating."

The airlines have been very critical of the National Air Traffic Service (NATS) for closing airspace on the basis of ash concentrations predicted by computer models. "[The crisis] is an extraordinary situation exaggerated by a poor decision-making process by national governments."

Is this fair? The famous economist, John Maynard Keynes, wrote a Treatise on Probability in 1921 in which he argued that sometimes it was impossible to accurately calculate the chance of an event, for example the chance that a plane will crash if it flies through an ash cloud. It is hardly surprising that this probability cannot be calculated; airlines themselves find it hard to predict the precise arrival time of their passengers (and baggage) at a specific destinations. But this inability to calculate probabilities does not mean that mathematics cannot be a great help in making the right decision.

Eruption of Eyjafjallajokull on April 17 2010. Image: Henrik Thorburn.

Essentially the airlines were facing extinction. Now, our mathematical model of bird behaviour, where the probabilities are known with certainty, suggests that the airlines would willingly take risks in order to survive. They would be prepared to fly through the ash cloud since, in their mind, there was a small chance of a plane crash compared to the large chance of their bankruptcy.

Crew and passengers were faced with the opposite dilemma to the airlines; they risked death, not by the planes being grounded, but by flying through the ash cloud. If the airline regulators had allowed the planes to fly, individuals, either passengers or crew, would be faced with an impossible decision: risk being involved in a crash or risk losing pay or an airfare. Seen from this perspective, the grounding of the airlines was acting for the "public good" by not forcing the public to make the difficult choice between losing money and risking life.

Mathematics is not about coming up with the "right" number that guides our decision making, rather it is about thinking clearly about a problem. The bird model demonstrates this point, it doesn't really matter what the precise probability of a plane crash is, what is important is making a good decision in the presence of uncertainty. What is meant by "good" is different if you are a passenger or an airline executive. The decision to ground the planes was "bad" from the airlines perspective, but for the rest of us, it was the right decision.

As a financial mathematician, involved in trying to understand and explain the credit crisis, what really struck me was a statement made in April, again reported by the BBC, by the airlines: "Airspace was being closed based on theoretical models, not on facts. Test flights by our members showed that the models were wrong." This statement reminded me of one published by The Economist in an article entitled No Defence on 31 January 2008: "[French banks] take an overly mathematical approach to risk. 'It may work in practice but does it work in theory? is the stereotype of a French bank,' says one industry consultant."

Both these statements reflect a common attitude that mathematical theory, because it cannot deliver "the number", is not really valid in informing decision making. But as we have seen, perhaps if bankers and regulators had taken more account of theoretical considerations, we would not have gone through the credit crisis.

The fact is, many problems society faces are problems that we cannot study through experimentation that will lead to absolute certainty. The only tool we have to get to the heart of the issues is mathematics.

It has been pointed out that no aeroplane has crashed as a result of flying though ash hundreds of miles from a volcano. This is a good thing and is a consequence of a mathematical understanding of the risks. Ignore the mathematics and airline executives might think "oops — that wasn't supposed to happen", while hundreds of families are thrown into grief following the crash of a plane. Do you feel lucky?

This article was written by Tim Johnson, RCUK Academic Fellow in Financial Mathematics, Herriot-Watt University, Edinburgh.