
Outer space: Wagons Roll

A couple of weekends ago I noticed that the newspapers were discussing proposals to introduce more restrictive speed limits of 20 mph in built-up areas of the UK and to enforce them with speed cameras wherever possible. Matters of road safety aside, there are some interesting matters of rotational motion that suggest that speed cameras might end up catching large numbers of perplexed cyclists apparently exceeding the speed limit by large factors. How so?
Suppose that a cycle is moving at speed V towards a speed detector. What we mean by this is that a wheel hub or the body of the cyclist is moving with speed V with respect to the ground.
But look more carefully at what is happening at different points of the spinning wheel. If the wheel doesn't skid then the speed of the point of the wheel in contact by the ground must be zero. If the wheel has radius R and is rotating with constant angular velocity w then the speed of the contact point can also be written as V-Rw. This must be zero and therefore V=Rw.
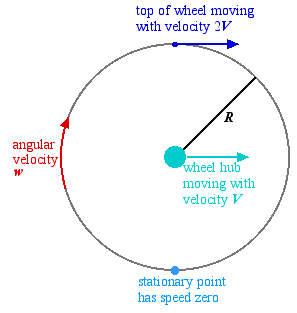
The forward speed of the centre of the wheel is V but the forward speed of the top of the wheel is the sum of V and the rotational speed. This equals V+Rw and is therefore equal to 2V. If a camera determines the speed of an approaching or receding bicycle by measuring the speed of the top of the wheel then it will register a speed twice as great as that at which the cyclist is moving.
An interesting one for m'learned friends perhaps, but I recommend you have a good pair of mudguards.
Did you manage to answer the puzzle posed in Outer space: Rugby and Relativity? If not, you can find the answer here!