
Overbooking: How to avoid plane rage
Overbooking became infamous overnight after United Airlines made a huge reputational error in dragging a customer off a flight to make way for what turned out to be a crew member. For anyone who missed this sorry spectacle, overbooking is the practice of selling more seats for a flight than exist on the plane. The ethics of overbooking were discussed at length in the days that followed the incident, but what about the maths? In this article we describe a simple, but effective model of overbooking that makes use of the binomial distribution.

Welcome on board?
The vast majority of people who buy a ticket for a flight intend to use it but sometimes circumstances get in the way. Easyjet states that 2.6 million of its passengers didn't show up for their flight in 2016 (around 3.5%), so if overbooking wasn't used, many aircraft would fly with empty seats. This results in reduced efficiency and less cash for the airlines. While you might not be worried about how much profit the airlines make, it's in everyone's interests that aircraft fly at full capacity.
Overbooking forms part of an area of mathematics called operational research, in which mathematical ideas are developed to solve optimisation problems in the "real world". These can range from business optimisation problems such as that described here, to optimal scheduling of operating theatres in hospitals, improving the efficiency of manufacturing lines, routing of vehicles, location of facilities, etc. For more information about operational research see the Learn about O.R. website.
Formulating the problem
Each person who buys a ticket has a probability that they will show up, which we label $p$ (so the probability they cancel is $q=1-p$). We're going to assume that these probabilities are the same for everyone and are independent of each other. Neither of these are perfect assumptions: certain classes of passenger are more likely to cancel than others, and if one person cancels, there is likely to be a higher chance that other people on the plane will also cancel (e.g. if there are major traffic problems just outside the airport many people might miss the flight). Nonetheless, the assumption makes a good first approximation. Let's assume that our aircraft has $C$ seats and the airline sells $y$ tickets, where $y \geq C$. The decision the airline has to make is how big to set $y$, that is, how many seats to overbook. But we'll first work out the probability distribution for the number of people who show up given that we have sold $y$ tickets, which we'll write as $Z(y)$.
Overbooking ruins holiday dreams.
If you're not familiar with the binomial distribution, take a look at this brief explanation to find out more.
Using the binomial equations, we can write the probability $P\left[Z(y)=z\right]$ that we have $z$ people showing up for the flight given we have sold $y$ tickets as \begin{equation} P\left[Z(y)=z\right] = {{y}\choose{z}} p^z (1-p)^{y-z}.\end{equation} Here the variable $z$ can take values from $0$ up to $y$.The first term in the expression above is the binomial coefficient as described here.
Using the model
We now have a set of equations that give us the probabilities of different numbers of people showing up for the flight. Here we consider the case where we want to restrict overbooking so that passengers are turned away on only a small percentage of flights.
For someone to be turned away on a flight, the number who show up, $Z(y)$, needs to be greater than the number of seats, $C$. We can write this in terms of the probability $P[Z(y)=z]$ defined in equation 1 above: $$P\left[Z(y)>C\right] = P\left[Z(y)=C+1\right]+ P\left[Z(y)=C+2\right]+...+P\left[Z(y)=y\right].$$ This expression comes from the fact that the probability of either one of two independent events occurring is equal to the sum of the probabilities of the individual events.An example
Let's see how this works for an example. The model is simple enough to be run easily on an Excel spreadsheet and you can download a copy here. Let's assume a cancellation rate of 5\% (so $p=0.05$) and correspondingly, a show rate of 95\% (so $1-p = 0.95$). For a plane of capacity $C = 100$, we might want to keep the probability of the number showing up exceeding capacity below 5\%. This would mean fewer than 1 in 20 flights needed to turn someone away. The table and graph below shows the relevant probabilities as given by the binomial distribution.
| Number of seats sold | Probability number of shows is greater than C |
| 101 | 0.56% |
| 102 | 3.4% |
| 103 | 10.65% |
| 104 | 23.08% |
| 105 | 39.24% |
| 106 | 56.22% |
| 107 | 71.21% |
| 108 | 82.67% |
| 109 | 90.40% |
| 110 | 95.08% |
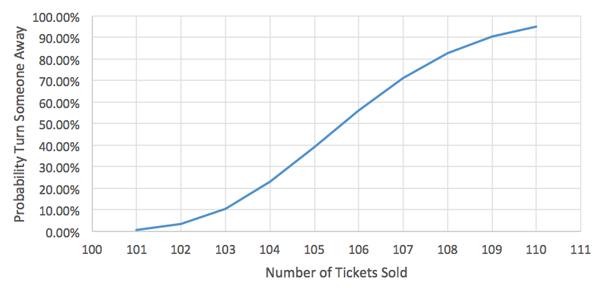
The graph shows the probabilities of someone being turned away.
Conclusion
Hopefully this gives some insight into how an airline makes a decision about whether or not to overbook and how to decide on the number of seats to sell. More advanced methods take account of the cost of turning away a passenger. If the compensation costs are very high, not to mention the damage done to the airline's reputation, overbooking is not going to be worthwhile, but if the cost is very low the airline might be happier to put it into practice. It's also necessary to know the market well and have a good estimate of the probability $p$ of a no show. Without that, the model is likely to suggest poor values for the number of tickets.
Abut the author
