
Picking holes in mathematics
 Kurt Gödel
Kurt Gödel
One thing that mathematics is equally loved and reviled for is its definite nature. Some people love the unerring hand of logic, but others loathe the lack of room for play. But once you penetrate to the very foundations of maths, the concept of true or false becomes a lot more slippery. The logician Kurt Gödel proved in the 1930s that if you set out proper rules for mathematics, excluding leaps of faith or intuition as admissible moves, you lose the ability to decide whether certain statements are true or false. And this isn't because you chose the wrong rules: for any set of rules, as long as they're strong enough to make sense of whole number arithmetic, there will be statements you can't prove or refute.
This is rather shocking and you may wonder why Gödel's result hasn't wiped out mathematics once and for all. The answer is that, initially at least, the unprovable statements logicians came up with were quite artificial and didn't touch on ordinary everyday mathematics. They certainly wouldn't come up in school homework or in the maths used to design aircraft wings. The vast majority of mathematicians leave these logical holes to the logicians and philosophers and get on with their work.
Some people, however, do wonder if there are more concrete examples of this so-called incompleteness of mathematics. Harvey Friedman, Distinguished University Professor at Ohio State University, is a pioneer in this area. "What is not addressed by [Gödel's results] is whether there's a clear and interesting problem that arises in regular maths which cannot be answered yes or no within [the rules] of mathematics we accept today," he explains. Friedman got his PhD from MIT in 1967 at the tender age of 18 and straight away became Assistant Professor of Philosophy at Stanford University — the youngest Assistant Professor ever. Not long after he changed camps and joined the maths community. He's devoted the last few decades to coming up with concrete examples of incompleteness.
The rules of play
Peano's axioms
Here's an informal version of Peano's axioms:
- 0 is a natural number
- Every natural number n has a successor s(n), which is also a natural number. (You can think of the successor of a number n as n+1.)
- For every natural number n the successor s(n) is not equal to 0.
- If for any two natural numbers m and n we have s(m)=s(n), then m=n.
- The final axiom concerns the method of induction, described at the end of this article.
But before we look at two of Friedman's approaches, let's examine what we mean when we talk about the "rules" of mathematics. To build a formal system of maths, you first need to decide what kind of assumptions you're prepared to accept without proof. These are your axioms. They usually involve pretty self-evident statements such as "0 is a natural number". You also need some rules of logical inference, for example "if x=y and y=z then x=z", and a language in which to speak about maths, consisting for example of mathematical symbols and a sort of grammar saying how to combine them. You then accept a statement written in your language as true only if you can prove it directly from the axioms, with no extra assumptions, using only your rules of logic.
It's up to you what kind of axioms you choose, but they should capture our intuition of what maths is about. A very neat set of axioms was developed in the 19th century by the Italian mathematician Giuseppe Peano. As you can see in the box above, Peano's axioms deliver a definition of the natural numbers and their ordering. The simplest formal system based on Peano's axioms is known as Peano arithmetic. It enables you to do all sorts of interesting maths, but there are also limitations to what you can say using Peano arithmetic, in particular when you try to make statements involving infinitely many numbers. Since Peano, mathematicians have come up with several other formal systems better equipped to deal with infinity. One of the strongest, and the most commonly accepted today, is based on the so-called ZFC axioms. (You can find out more about the ZFC axioms in the Plus article Searching for the missing truth.)
Gödel's incompleteness
Formal systems seem to provide the perfect framework for proving everything there is to prove within mathematics, but as it turns out, they come with limitations. Gödel's first incompleteness theorem says that within any formal system that's strong enough to express arithmetic, is free of contradiction and whose axioms can be recognised by a computer algorithm, there are statements, expressed in the system's own language, which you can neither prove nor refute. You can of course try to settle such an undecidable statement by adding whatever axioms are necessary to prove it, but according to Gödel's result, other undecidable statements will pop up elsewhere.
The most famous undecidable statement within the ZFC axioms is the continuum hypothesis. It's undecidable in a very profound way, but it's concerned with rather strange infinite sets of real numbers that working mathematicians rarely ever come across. "In the normal course of mathematics one considers much more regular sets of real numbers," explains Friedman. "In fact, these days, one often looks at things one can simulate on a computer, which are several layers of magnitude more concrete."
Over the years, Friedman and others have come up with examples of incompleteness that feel a lot more concrete than the continuum hypothesis. They still don't put ordinary maths into any immediate danger, but they are striking nevertheless, especially because you don't need to have studied advanced maths to get an idea of what they're about.
Incompleteness from finite trees
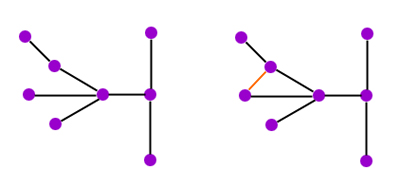 Figure 1: The network on the left is a tree, but the one on the right is not because it contains a cycle.
Figure 1: The network on the left is a tree, but the one on the right is not because it contains a cycle.
One example is a result Friedman proved in 1982 concerning what mathematicians call trees. In maths a tree is a network which doesn't contain any circular paths. It's made up of a collection of interlinked nodes, with only one path linking any two given nodes. See figure 1 for an example.
Trees crop up in many different contexts, including computer science: if a computer programme makes a yes/no decision at every step of some process, then its combined options can be presented as a binary tree (see figure 2). Another example is genetics, where trees are used to describe the evolution of species. This context has actually produced some some very hard (though not undecidable) mathematical questions (see the Plus article Reconstructing the tree of life). So in terms of concrete incompleteness, trees are a good place to look.
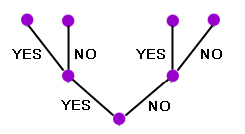 Figure 2: A binary tree.
Figure 2: A binary tree.
One natural question to ask is whether a given finite tree (that's a tree with finitely many nodes) contains a smaller given tree, as illustrated in figure 3. Taking this a step further, if you've got a whole collection of finite trees, what are your chances that one of the bigger ones contains one of the smaller ones? Surely this chance should increase as your collection of trees gets larger? In the 1960s the American mathematician Joseph Kruskal proved a result which confirms this intuition: as long as you've got infinitely many finite trees in your collection, you can be sure that one of them contains another.
This result sounds straight-forward enough, so can you prove it using Peano arithmetic? The first problem you encounter is that you cannot even state the result in Peano arithmetic — the language lacks the words you need to talk about arbitrary infinite collections of trees. However, if your infinite collection can be generated by some finite set of instructions, that is, if it can be generated by a computer, then Peano arithmetic can talk about it. Friedman showed that the sentence "in any infinite collection of finite trees that can be generated by a computer, some tree is contained in another" can be stated in Peano arithmetic, but that it can be neither proved or refuted.
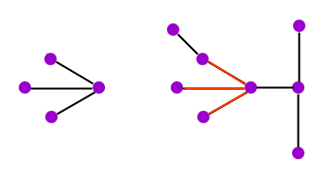 Figure 3: The tree on the left is contained in the tree on the right.
Figure 3: The tree on the left is contained in the tree on the right.
Perhaps this isn't surprising, since the result still talks about an infinite collection of things and Peano arithmetic is not well-equipped for dealing with infinity. However, Friedman managed to produce a finitary version of this statement. Suppose you're looking at a finite sequence of finite trees. Then as long as the sequence is large enough and the number of nodes in the trees doesn't grow too fast as you move along the sequence, you can guarantee that there are two trees with one containing the other.
This result can be stated in Peano arithmetic, but as Friedman showed, its proof is beyond the capacity not only of Peano arithmetic, but also some considerably stronger systems.
Once you enlist the full power of the ZFC system, this particular result does become provable. But Friedman has since started to work on more general forms of networks and obtained stronger results . "I have the beginning of a structure theory [for aspects of certain networks] in which there are theorems that can only be proved using some ridiculously strong new axioms," he explains. These axioms go way beyond Peano arithmetic and also ZFC. Whether the undecidable results in question will ever cross the path of applied mathematicians or computer scientists remains to be seen, but given their distinctly computational flavour, the potential is certainly there.
Incompleteness from functions
Another fruitful approach to finding concrete incompleteness comes from functions defined on sets of numbers. Suppose you're looking at a function of two variables, for example $$f(x,y)=xy,$$ defined on the set of whole numbers (meaning that $x$ and $y$ both have to be whole numbers). The output of your function will also be a whole number, eg $$f(2,7)=2\times 7=14.$$ In fact, the combined output for all choices of $x$ and $y$ gives you the entire set of whole numbers, since every whole number can be written as the product of two others. Now what happens if you restrict your inputs to the set of even whole numbers? Then the output consists of numbers which are multiples of 4: if $x$ and $y$ are even, you can write them as $x=2m$ and $y=2n$ for some whole numbers $m$ and $n$, so $$f(x,y)=4nm.$ In other words, the output misses out all the numbers that are not multiples of 4. You can phrase this problem in more general terms: given any function $g$ (of two or more variables) can you always find an infinite set $A$ (in our example that was the set of even numbers) such that if you restrict your inputs to $A$, your output misses out some of the whole numbers?
 Harvey Friedman
Harvey Friedman
You can't state this question in Peano arithmetic, but you can talk about it in a close associate of Peano arithmetic, which allows you to talk about infinite sets of natural numbers. However, Friedman showed that you cannot decide the answer to this question even within the associate system. The statement "yes, you can find such a set $A$" is undecidable within this system. Friedman has taken this result as a template to find more examples of concrete incompleteness, creating an area of maths he calls Boolean relation theory. The general idea is to ask if given several functions, rather than just one, you can find several infinite sets that guarantee a certain configuration of outputs. Friedman has shown that even when you're looking at just two functions and ask for a configuration of outputs involving just three sets, you already run into logical difficulties. He's come up with a collection of explicit results, involving a basic class of functions, that are undecidable in the ZFC system.
Richard Elwes, a mathematician at the University of Leeds, believes that this work is an important step towards concrete incompleteness. "The situations described by Boolean relation theory are indisputably elementary, and (perhaps somewhat disputably) they seem natural," he says in an interesting blog post on the subject. "What is more, they are ripe for generalisation. This may well represent a door through which questions of provability enter mainstream mathematics, not in ones and twos, but in truly significant quantities."
But what does it mean for maths?
Although Friedman's approaches are promising, it may be a very long time until we know just how far-reaching they are. As he himself concedes, "The extent to which we have concrete incompleteness and what the wider implications are, will not be clear for hundreds of years, if not longer."
But what will happen when undecidable questions finally do hit the mainstream? Will mathematics collapse like a house of cards? The answer is probably no, since there's always the option of adding new axioms to ZFC, which strengthen the system and extend our intuition. These won't do away with undecidable statements altogether, that's Gödel's incompleteness result, but if chosen correctly, they might stifle some particularly prolific sources of concrete incompleteness.
Just adding new axioms to sort out your problems might feel like cheating, but there are precedents. Take, for example, a technique known as mathematical induction, commonly used to prove statements about all the natural numbers. The idea behind induction is simple: you first prove your statement is true for the first natural number, 0, and then you prove that if it's true for one natural number, it's also true for the next one along. In this way, the numbers succumb to your statement one by one, like a row of dominoes.
 Under induction numbers succumb to your statement one by one, like a row of
dominoes.
Under induction numbers succumb to your statement one by one, like a row of
dominoes.
Induction feels like second nature to mathematicians today, but as Friedman points out, it's a rather late development in mathematics: the Greeks, for example, did not understand it well. The fact that induction is a valid technique can itself be regarded as an axiom. In fact, Peano arithmetic contains such an axiom for induction. It would have been bafflingly unnatural to the ancient Greeks, but today's mathematicians don't bat an eyelid at its appearance.
In a similar way, there maybe another, even more profound principle that's not accessible to current intuition, but that will reveal itself one day. "This may be even more powerful than induction has proved to be," says Friedman, "a new technique that will greatly strengthen existing results, solve existing problems and create new mathematics of an unexpected kind."
So even if incompleteness does one day infiltrate normal maths in a profound way, there's a chance that it comes with its own solution in the shape of candidates for new axioms. Whether they'll be accepted by mathematical philosophers will depend on how natural they feel given the current state of understanding, and how many problems they help to solve.
About the author
Marianne Freiberger is co-editor of Plus. She interviewed Harvey Friedman in Cambridge in November 2010.
Further reading
If you liked this article, you might also want to read Searching for the missing truth.
Comments
Anonymous
So what that certain statements are undecidable? That isn't a barrier to maths or to logic, they are just labelled as undecidable and we can reason about them based on that knowledge.
Undecidability is an advancement in mathematics, and can probably be used for important things like encryption, we should stop thinking about it as a negative of mathematics, it is a strengthening of our understanding of logic, not a weakening by any means.
Anonymous
If we take Heinz von Foerster's theorem that, "Only those questions that are in principle undecidable, we can decide" (original emphasis, see "Through the Eyes of the Other, von Foerster, 1991) then the determination that certain mathematical statements are undecidable is a rather important discovery. Taken together, von Foerster and Friedman might mean that mathematics can finally decide.
Anonymous
Nice article, though I have a question: I might well misunderstand the whole subject, but doesn't "concrete incompletness" show up in many problems related the length of arbitrary programs like in the halting problem or the kolmogorov complexity, some of them with many potential practical applications were they not undecidable?