
Ping pong balls, infinity and superpowers

Infinity is a bendy concept that can lead to all sorts of paradoxes.
In this article I plan to hit you with not one, not two, but three bamboozlers! And they're real beauties. It's the concept of infinity that will mess with your minds. I think you'll have a lot of fun recognising just how crazy and exciting a concept it is.
First of all, I'd like you to think about the size of infinite collections of things, or infinite sets, as they are called. The size of a set is simply the number of items it contains. Two sets are the same size if there is at least one way to match each element of one set with exactly one element of the other set, such that no elements in either set remain unmatched.
That makes perfect sense. The set $\{1, 2, 3 \}$ is the same size as the set $\{A, B, C\}$ because we can match $1\leftrightarrow A$, $2 \leftrightarrow B$, and $3 \leftrightarrow C.$ (There are, of course, other ways to match them up, but we only need to find one.)However, things get more interesting when we deal with infinite sets.
As an example, think of the set of all positive whole numbers $\{1, 2, 3, 4, ... \}.$ It is the same size as the set of all even numbers $\{2, 4, 6, 8, ... \}.$ As crazy as it sounds, throwing away every second element of the first set still leaves us with a set of the same size, because we can match up the elements like so: $1\leftrightarrow 2,$ $2 \leftrightarrow 4,$ and $3 \leftrightarrow 6$ etc. Any element in the first set has a single match in the second set, namely its double, and similarly any element in the second set can be matched with half its value in the first set. No element is left unmatched, and so, strange as it may seem, the sets are the same size. Other sets of the same size as all positive whole numbers include the sets of all odd numbers, all multiples of 10, and even all fractions. (Such sets are said to be countably infinite. See here to find out more.)
I am now going to describe a thought experiment that will illustrate some unexpected consequences of this fact.
Bagging ping pong balls
Let me introduce Clark. He has a superpower that enables him to carry out what mathematicians call a supertask — that's a task that requires an infinite number of steps to be completed in a finite time. In our case, the time will be exactly one hour, starting at 11:00 and finishing at 12:00.
Clark has an infinite supply of ping pong balls, numbered in order from 1, and a bag to put them in.
At 11:00 he takes the first ten balls, numbered 1, 2, 3, … 10, and places them in the bag. He then removes the ball numbered 10 from the bag, leaving the other nine behind. Easy. No superpowers needed yet, and Clark should relax for a while and have a cup of tea, because it's going to get harder.
After waiting 30 minutes, at 11:30, Clark places the next ten balls, numbers 11, 12, … 20, into the bag, and removes ball 20.
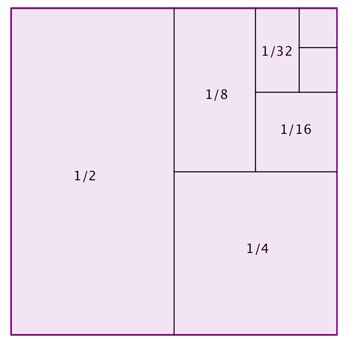
This picture shows why the sum converges. Suppose the square has area 1, and divide it into two equal halves, then divide one of those halves in half again, then divide one of the two new pieces in half, etc, ad infinitum. The pieces you get have areas 1/2, 1/4, 1/8, 1/16, etc — and they fit exactly into the original square, which means their areas must sum to 1.
After waiting a further 15 minutes (and so at 11:45) he places balls 21 to 30 in the bag, and removes ball 30.
Clark keeps doing this, always adding the next ten balls then removing the 10th one, but waiting only half the previous wait time each step.
Clearly Clark will need to do this an infinite number of times to get through the infinite supply of ping pong balls. So will he ever finish?
The answer is yes. If we add up the intervals Clark waits before putting the next lot in the bag, we get the sum (in fractions of hours): $$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...$$
This sum converges to the number 1: that is, every term you add gets you closer to 1, and you can get arbitrarily close to 1 by adding sufficiently many terms (see the figure on the left). Crucially, the sum doesn't exceed 1, so the whole process of ball bagging, although it involves an infinite number of steps, only takes one hour to complete. (And thanks to his superpower, Clark can carry out the infinite steps).
At 12:00, when the process is complete, how many ping pong balls are in Clark's bag?
Well, at each step Clark adds nine balls, and there are an infinite number of steps, so there will be an infinite number of balls in the bag. In fact, out of all the positive integers, only those balls numbered with a multiple of 10 will not be in the bag. That was pretty obvious really. No bamboozling so far — just a little bit of concentration required to think clearly about the infinite process.
So let's add a bit of confusion.
Bamboozler #1
Suppose, while Clark is doing the experiment his friend (and fellow superhero) Bruce is also bagging an infinite number of ping pong balls. However, he uses a slightly different strategy.
At 11:00, Bruce takes the first ten balls, numbered 1, 2, 3, … 10, and places them in a bag, but he removes ball number 1 from the bag. Then, at 11:30, he places the next ten balls, numbers 11, 12, … 20, into the bag, but removes ball number 2. After 15 more minutes, at 11:45, he places balls 21 to 30 in the bag, and removes ball 3. And so on, each step adding the next ten balls, but removing from the bag the ball with the smallest number.
Is Bruce's approach essentially the same as Clark’s? Well, each time he is adding ten balls and removing one, so it certainly appears to be so.
At 12:00, when Clark and Bruce compare their respective bags of ping pong balls, what do they see?
We know that Clark's bag contains an infinite number of ping pong balls, but, incredibly, Bruce's bag will be empty! Yes — empty. Every ball will have been removed.

Lots of balls.
Think about it; what ball numbers can possibly remain? The balls are numbered 1, 2, 3 … to infinity, but each number corresponds to one of the infinite adding-removing steps and so each ball will have been removed. For example, ball 20 was removed on step 20, ball 1529 on step 1529, ball 1327821 on step 1327821. They're all gone!
Wow! That's mad. Clark has an infinite number of ping pong balls, and Bruce has none. (For an interesting twist, suppose the experiment used pound coins instead of ping pong balls, and you were allowed to keep whatever coins remained in the bag at 12:00.)
But it's even weirder when you think what happens if they check before the time is up.
Bamboozler #2
Suppose Bruce and Clark check the bags every step instead of just at 12:00. What do they see?
Every time they check, prior to exactly 12:00, they will see they have the same number of ping pong balls. It's true — every single time they check, the number of balls will be exactly the same. Only at 12:00 precisely, when the infinite process is completed, will there be a difference — and what a difference there will be! It will be like all of Bruce's ping pong balls just vanish.
Bamboozler #3
Understanding and calculating the outcomes for Clark and Bruce depended on the numbering of the balls. So let's now suppose a third superhero, Diana, was there and doing the same thing — ten balls in, one ball out each step. However, Diana's ping pong balls were not numbered and were completely indistinguishable.
At 12:00, how many ping pong balls will be in Diana's bag?
Sorry — no answer here. At this point we've pretty much crossed from mathematics into philosophy, so this question's for you to think and argue about.
Discussion
Maybe you think this is all too unrealistic, because supertasks are not actually possible? Well, that doesn't really matter in mathematics. It is possible to think about them, reason about them, and study them. And this is true for many things in maths.

Whether or not triangles and supertasks are real is a question for philosophers such as Plato and Aristotle, shown here in a painting by Raphael.
For example, do you believe in triangles? Are they real? They're not. There is no such thing in the real world as a triangle. They exist only in our mathematical minds, just like infinity and supertasks and many other mathematical concepts. Every "triangle" we see is just an approximation — the sides are not exactly straight; the angles do not add exactly to 180 degrees etc. But this does not detract from the importance and necessity of studying triangles and their properties as mathematical entities.
So how does our ping pong problem relate to the mathematics of infinity and infinite sets?
In each case we are adding an infinite number of balls and removing an infinite number of balls, but $\infty- \infty$ is undefined: it can be made to have many different answers. And that is indeed what we have found. The ping pong problem also illustrates the difference between showing the set of all positive integers and all multiples of 10 are the same size by lining them up and matching the elements (this is essentially Bruce's strategy): \begin{eqnarray*} 1 & 2 & 3 & 4 & ... \\ \updownarrow & \updownarrow & \updownarrow & \updownarrow & ...\\ 10 & 20 & 30 & 40 & ...\end{eqnarray*}compared to removing all the multiples of 10 from the set of all integers, and leaving an infinite set behind (this is Clark's strategy):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | ... |
Some further things to ponder
- You can construct a process that will leave any positive integer amount of balls in the bag by switching from Clark's strategy to Bruce's strategy at an appropriate time. Try and come up with a strategy that leaves exactly five balls in the bag.
- When Diana is performing the experiment, the balls are indistinguishable. Consider her $kth$ adding/removing step.
- What is the probability of a random ball remaining in the bag after this step?
- What is the probability of a random ball remaining in the bag after this step and the next step?
- Can you use these results to calculate the probability of a random ball remaining in the bag after infinite steps?
- Does this calculation provide a way to answer the question of how many balls Diana has remaining after infinitely many steps?
- In Bruce's case, how does the final ball get removed to leave none, when he has always added 10 balls immediately before the removal?
-
Imagine there was a gremlin in Clark's bag, and when he tried to remove ball 10, the gremlin erased the 0 making it ball 1 and added a 0 to ball 1 (that is still in the bag) to make it ball 10. He did the same when Clark removed ball 20 — making it 2 and changing the other 2 into 20, and so on with ball 30 and ball 40 etc.
Does this gremlin's renumbering mean the final number of balls in Clark's bag changes to 0 (like Bruce)?
- If it does, how could it? He's still removing exactly the same balls!
- If it doesn't, what are the numbers on the balls left in the bag?
- Supertasks are clearly not physically possible. Do you think these paradoxes show that supertasks are not even logically possible?
About the author

Ken Wessen has PhDs in Theoretical Physics and Human Biology, and a Graduate Diploma in Secondary Mathematics Education. He has taught both at university and in high schools, but most of his working life has been in investment banking, developing algorithms for automated trading of equities and foreign exchange. In his spare time he writes free software and develops online activities for mathematics learning at The Mathenaeum.
Comments
Anonymous
nice expose, Ken!
how about you leave 1/2 ball in the bag: at the kth time step, change the count of balls in the bag by (-1)^k, i.e., put a ball in the first step, remove one ball in the second step, add one at the third step. 1-1+1-1+... = 1/2, or:
leave -1/12 balls in the bag: at the kth time step, add k balls to the bag. 1+2+3+... = -1/12.
what breaks the balls into pieces to make this happen? what if the balls are 'atoms' ('indivisible')?
Does that mean that the process is illogical for indivisible things? Or, does it mean that nothing is indivisible? If 'balls' were instead distinct fixed-volume elements of space, and the bagging operation was merely the process of labeling such elements, would the process generate an 'address book' for the entire universe? Does space need to be infinitely divisible for this to be logical?
Anonymous
Thanks for this article. That's a pleasant way to make our brains running a bit.
Firstly, I would disconnect the convergence of the duration and the object that Clarck and his friends build. Having a converging time does not mean necessary that the mathematical operation leads to a defined object.
If you are in the frame of the set theory with ZFC axioms, Clarck build an actual set of balls with the direct application of the axiom of choice : from an infinite collection of set of 10 balls 10n to 10n+9, you extract all the 10n. Bruce does not.
Anonymous
Fascinating piece, clearly explained - thankyou!
Perhaps in a few weeks some hints at solutions for the items to ponder?
Great use of DC's greatest heroes, too.
ikajula
elsa frozen
Leslie.Green
This is essentially Littlewood’s paradox from his 1953 book. In it the underlying problem concerns points, and parenthetically (and in the footnotes) he discusses null sets of measure zero.
He ends up with an enumerable set of points (countably infinite) which has a Lebesgue measure of zero. I think he is just making a technical joke equating zero balls with a measure zero set of points. It is just too technical for most people to get (including me, until recently).
http://lesliegreen.byethost3.com/articles/Littlewood.pdf