
What is infinity?

In a sense we all have an inkling of what infinity is. It's something that characterises things that never end. A never-ending Universe, or a never-ending list, like the list of natural numbers 1, 2, 3, 4, .... . No matter how long you count for, you can never reach the end of all numbers, and you can't reach the end of an unending Universe even if you travel in the fastest spaceship. This kind of infinity is what the ancient Greek mathematician Aristotle called a potential infinity: it's definitely there, but you will never actually meet it face-to-face. You just can't get to the end of those never-ending lists or expanses.
Aristotle also thought of another kind of infinity, called an actual infinity. This would be something you could measure, say the temperature of an object, in a particular place and time. Nobody has ever seen such an actual infinity, and indeed Aristotle thought that actual infinities don't exist in the physical world. To this day, physicists don't know whether he was right or wrong.
Keep counting
So let's stick to potential infinities; those that characterise something unending. We already mentioned the list of natural numbers as an example. But now think of an infinitely long straight line; a line that starts at a point just in front of you and stretches on forever, straight ahead. Is the infinity it represents the same as the infinity represented by the natural numbers?
Intuitively you might think that the two are different. The natural numbers are separate, discrete entities, while the line forms a continuum. You could place the natural numbers along your line, at distance 1 metre apart. This gives a sense that there is somehow more to the infinity of the line than to the infinity of the natural numbers: it is able to fill the gaps between the numbers.
Mathematicians agree with that intuition. They distinguish between countable infinities and uncountable ones. The natural numbers form a countable infinity and that makes sense, as you could count through all of them if you had an infinite amount of time. A group of infinitely many people also qualifies as a countable infinity. That's because (with an infinite amount of time) you could make a list of all the names, each name taking its own place on the list, and then you could count through them, just as you can count through the natural numbers. In general, an infinite collection of objects forms a countable infinity if you can list the objects one by one, with a place on the list for every object and one object for every place on the list.
What about the infinitely long straight line? It is also made up of infinitely many objects: in this case the objects are points on the line. If you imagine this line as an infinitely long ruler, then each point comes with a number: the starting point of the line comes with the number 0, the point half a metre along comes with the number 0.5, and so on (the collection of numbers you get from the ruler are called the positive real numbers). Can you make a list of those numbers to show that they also form a countable infinity?

One approach would be to order those numbers by size. But that quickly gets you into trouble. Clearly the first number should be 0, but what about the second one? You could try 0.1, but then, 0.01 is smaller than that, so it should come before 0.1. But what about 0.001? For every number you might designate as taking the second place on the list you can find a smaller one (you simply insert an extra 0 after the decimal point). So listing those numbers along the ruler by size is hopeless.
Could there be another way of listing them? The answer is no. There is a reasonably straight-forward argument which shows that any list of positive real numbers definitely misses out at least one other positive real number. You can never make a complete list. This shows that the infinity represented by the infinite straight line (or, equivalently, the positive real numbers) is an uncountable infinity.
Which infinity is bigger?
What about the idea that the infinity of the infinite line is somehow "bigger" than the infinity of the natural numbers? One way of comparing the size of finite collections of things, if you can't be bothered to count, is to see if you can match them up exactly. Think of a number of chairs and a number of people. If there is a chair for every person and no chairs are left over, then you know that there must be the same number of chairs as people. If there are chairs left over, then you know that there are more chairs than people. And if there are some people left standing, you know that there are more people than chairs.
You can extend this idea to infinite collections of objects. If you can match the objects in collection A to the objects in collection B exactly, with every object in A corresponding to exactly one object in B and vice versa, then we say that the two collection have the same size or, as mathematicians put it, the same cardinality. We have already seen this in action with our infinite group of people above. By listing them one by one we have actually matched them up exactly with the natural numbers: for every person there is exactly one natural number (their place on the list) and for every natural number there is exactly one person (the one occupying the place on the list given by that natural number). This is why we say that the group of people and the natural numbers represent the same kind of infinity — a countable one.
Going back to points on the infinite line, however, it turns out that any attempt to list them (to match them exactly with the natural numbers) misses out at least one point. This is why we say that the cardinality of the line (an uncountable infinity) is greater than the cardinality of the natural numbers (a countable infinity).
Countable confusion
Intuitively, uncountable infinities appear more unwieldy and tricky than countable ones and in mathematics they often are. But this doesn't mean that countable ones are straight-forward. As an example, think of all the even numbers 2, 4, 6, 8, and so on. There are infinitely many, but what is the cardinality ("size") of that infinity compared to that of all the natural numbers? Surely it should be half as big?
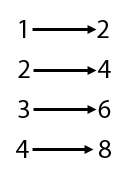
The answer is no. We said that two infinite collections have the same cardinality if the objects in one can be matched up exactly with the object in the other. It's pretty easy to match all the even numbers exactly with all the natural numbers:

Georg Cantor
So the cardinality of the even numbers is the same as that of the natural ones. If this seems weird then perhaps the next result is even weirder. It's possible to show that all the rational numbers (that is, all the fractions such as 1/2 or 5/6) can also be listed; that is, they can be matched exactly with the natural numbers. So even though there appear to be many more fractions than natural numbers (there are infinitely many fractions between any two successive natural numbers) the two sets of numbers have the same cardinality.
The eminent Galileo Galilei discovered such strange facts about infinity back in the 17th century and thought they were so weird, it put him off thinking about infinity claiming that "we cannot speak of infinite quantities as being the one greater or less than or equal to another". Over 200 years later, the mathematician Georg Cantor picked those ideas up again, undeterred by their weirdness, and went much further. He discovered a whole tower of infinities, each one larger than the other. The infinities of the natural numbers and the infinity of the line are only two of them.
All of this was concerning potential infinities, those that describe never-ending lists or expanses. What about those actual infinities? And do any of these infinites actually exist in the physical world? To find out about all this and more, see the articles and podcasts in our infinity package.
About the author
Marianne Freiberger is Editor of Plus.
Comments
Anonymous
So, you are using numbers to count and characterize other groups of numbers (sizes and cardinalities). Got to be suspicious about the conclusions drawn. It would seem to be like using the lens of a telescope to examine the optics of another. Invisible distortions and characteristics of the former would be confused with characteristics of the observed latter telescope. Are we raising ourselves by our own bootstraps? A mathematician thinks logically, but I am not formally trained. So, tell me how I am wrong.
Anonymous
Not a professional math person here, but I studied Cantor in the past. I think one thing he would point out is that the analogy is imperfect. In the sense that numbers are counting and characterizing other numbers, the telescopes would only have to be able to see and be seen by one other telescope (or not). It is the existence (or not) of a 1 to 1 correspondence between telescopes that matters, not the quality of the images they produce. In fact, as long as the telescopes can be paired in some way, one never need look through them at all. In the same way, numbers do not do the heavy lifting in determining cardinalities. That job is left up to "functions" (in the mathematical sense).
The article started to explain this on the "even numbers" situation, but didn't illustrate the importance of functions. Remember, what is needed is a 1 to 1 correspondence between the numbers. As I remember, cardinality is tested (or defined) in the following manner: If a 1 to 1 correspondence exists between two sets of numbers (in this case 2 infinite sets), then those sets have the same number of members, and hence the same cardinality. If no such correspondence exists, then one set has more members, and a higher cardinality. So what is (one possible) 1 to 1 correspondence between the natural numbers (x) and the even numbers (y)?
y = 2x
For any natural number (x), there is one and only one possible value for (y) that satisfies the equation. Equally important, for any even number (y), there is one and only one (x) that satisfies the equation. Since both of those conditions are true, a 1-1 corresp. has been found to exist, meaning there are the same number of naturals as evens: so both sets of numbers are characterized as having the same cardinality.
It is a bit trickier (and space consuming) to show the 1-1 corresp. between the natural numbers and the rational numbers. It's even worse to show no such correspondence can exist between the natural and irrational numbers. If intrigued by this article, there are plenty of resources out there on it - for all levels of interest and aptitude. Just be warned: Cantor went much deeper than I or the article could ever hope to...and for his troubles, he also went insane.
Anonymous
I love square numbers, but taking them to infinity has me floored. For every number, there is a corresponding square, so 1 to one correspondence in that direction. But there are many many numbers which are not squares - 2,3,5,6,7,8 for which there is no correspondence with the natural numbers, so how can there be the same cardinality? One set is so much greater than the other this side of infinity! Can you save my sanity?
ES
Anonymous
Opps....anonymous fail...no child left behind, yeah right :)
Anonymous
We normally count in bases, usually base ten. When you run out of the ten counting symbols or digits 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, you can carry on using them by doubling them up: 10, 11, 12, and when you run out of those then trebling up: 100, 101 . . . for as long as you live if you feel like it. You can count in quicker jumps too: from 7 to 13 by a jump known as adding the number 6, from 13 to 42 by adding 29. This jump is a bit more complicated because you have to carry a number, 1, at the same time.
But what if we had an infinite base? That means using a new symbol every time, no recycling old ones. So a very big quantity that takes maybe hundreds of digits to count up to in base ten would only need one in base infinity, say a smiley face. And all our jumps could be made without having to carry any number. So you can get from smiley face to say lightning bolt just by adding lollipop. Of course we might need a special publicly accessible book or database to keep all these digits in so everybody knows what you're talking about, but that wouldn't have to be actually infinite in size - just say several trillion in the early stages and continually growing as required. (So it's a bit like the Aristotelian potential infinity mentioned in the article) Every time somebody counted beyond the existing latest symbol they'd be legally or at least morally obliged to add the new symbol thus created to the database. Same as a copy of every printed book has to go to the Library of Congress.
What about the symbol for infinity then? Can it go in The Book? Yes, maybe but this time every new symbol would have to be entered before rather than after it. It could be a second order symbol for any as yet unadded counting symbol, rather like those three dots I used at the beginning . . . Or maybe not a book, but a book end.
Anonymous
Cool thinking! If we have an infinite line of pebbles but don't assign identities to any pebble then our system could be defined as orderly but simple.
If on the other hand as you described we assigned an entirely distinct identity to every pebble in the infinite system it could be defined complex but chaotic.
By using a number base and encoding every pebble we split this situation but still have to deal with some chaos and simplicity so that we can achieve order and complexity.
I reckon doughnut base, yum
Anonymous
I'm intrigued by your reply to my "Base Infinity", though still somewhat unfamiliar with the mathematical ideas of chaos and complexity.
In Base 10 for example, with its ten distinct symbols irreducible to each other, the new symbols successively created on adding 1 to each of 0, 1, 2, 3, etc, are arbitrary and unpredictable. So thus far the system is chaotic. 0nly when we come to start doubling up by adding 1 to 9 to get 10 do rules supervene and things get orderly. So in base infinity chaos always rules since every new symbol is unpredictable and can't be determined by any previous one. Right?
(Does that also apply to donut as a symbol, or are you thinking of some kind of torus structure?)
Chris G
Anonymous
We have a base infinity, in which every number has a unique designation. This is the name we call each number - eg twenty-one. There is no duplication, yet each new "symbol" can be determined by the previous one, so no chaos. Right?
Anonymous
21 is a pair of symbols, usually from a limited base set of ten. Each of them, 2 and 1, were previously used singly, and are subsequently recycled by being put together to designate yet another number in accordance with a rule. My point about base infinity is that we'd never get this. Every number would have a brand new single symbol that's specially invented or arbitrarily chosen for it rather than formed from a combination of old ones, and so in that sense the symbol would not be determined by what's gone before.
An absurd situation in practical terms, however I don't know enough of mathematical chaos theory to say if that makes such a sequence chaotic. That was the question I was putting to the (other?) anonymous contributor to this thread, and to anyone else.
Chris G
Anonymous
Further to my submission that the names of the numbers are a unique designation with no duplication, I should have specified that the name is written in longhand, so that the line is contiguous. Thus the "squiggle" in longhand of "twentyone" would be a unique squiggle. Although the last three letters are identical to the last three of "thityone", this is no different from saying that the lower half of the squiggle "3" is the same as the lower half of "5", yet we consider these to be different.
Anonymous
This might be of interest..
https://www.google.com/url?q=http://www.harekrsna.com/sun/editorials/11…
Anonymous
I try to imagine that circles & spheres are the signature of a unitary perfect infinity. And does this perfect unit actually exist in the universe that we see. Well even a neutron star or the Avogadro sphere have some small deviation.
Mobius shapes and the torus offer some other insights, The torus especially seems applicable to some of larger and smaller scale events and objects around us.
A fractal is in a way independent of the measure of size, could infinities be fractal?
Could infinities be embedded within each other in a hierarchy?
Great thought provoking article!
Anonymous
In a comment on Rachel Thomas's recent article "The Fibonacci sequence: a brief introduction" I mention a companion sequence to Fibonacci's rabbits which I now know to be called "Narayana's cows" (OEIS A000930). This is defined by OEIS as
a(0) = a(1) = a(2) = 1; thereafter a(n) = a(n-1) + a(n-3)
and goes 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41 for the first twelve terms.
This sequence differs from the more famous Fibonacci by starting with three 1's instead of two, which means there’s a delay of 3 years (or months or whatever you want the unit period to be) instead of 2 before these animals produce offspring. The delay, or D number for Narayana’s cows is 3,as given by the final term in that definition: a(n-3). For the Fibonacci sequence however the defining equation is a(n) = a(n-1) + a(n-2), so the Fibonacci D number is 2.
In a sequence where D is 1 then we get a(n) = a(n-1) + a(n-1), leading to a(n) = 2(a(n-1)). This simply means the sequence starts with a single 1 and doubles each time. A lot faster.
What if D were 0? Would that make the reproduction rate inconceivably, perhaps ifinitely, fast? Rabbits or cows giving birth to more rabbits or cows, which as soon as they’re born immediately and simultaneously produce yet more rabbits or cows and so on?
Yet the equation for this sequence, a(n) = a(n-1) + a(n-0), suggests the opposite. It solves as a(n-1) = 0, which if true for any a(n) in the sequence, means the sequence consists solely of 1’s. This in turn seems to characterise an infinite D such that no offspring is produced at all, bearing in mind that the first reproduction can only occur with summing of the first and last of the 1’s, as becomes apparent in the Narayana case.
Maybe both answers amount to the same thing, or maybe to the two different kinds of infinity – actual and potential. All suggestions gratefully received.
Chris G
Anonymous
I'm embarrassed to report what must be a typical error in my comment "InFibity". I misread the expression a(n -1) = 0 as a(n) - 1 = 0, resulting in a sequence consisting solely of 1's. In turn this suggests an unending or infinite delay before reproduction takes place. Whereas if the delay is zero one would expect the reproduction to be explosively fast, infinitely fast if it takes place in an instant.
So I'd be grateful if anyone could suggest what, if any, sequence is generated by a(n) = a(n-1) + a(n-0) in which the delay is zero. A sequence consisting solely of zeroes? What would that mean?
And what if the delay (D) number were a negative quantity? An anticipation? If D was -1 the sequence generating algorithm would be a(n) = a(n-1) + a(n--1), that is every number is formed by adding the two on either side of it. Given the first two terms 0 1, then we'd get a repetitive sequence going 0 1 1 0 -1 -1 0 1 1 0 -1 -1
Anonymous
For D = 0,
we have: a(n) = a(n-1) + a(n-0)
Which is a(n) = a(n-1) + a(n)
i.e. 0 = a(n-1) + 0
Which is just like saying a(n) = 0
So in that case you're right, a sequence of only zeros, as to what that means, I'm not sure, I guess the model breaks down a bit here.
For D < 0 interesting things happen.
For the sake of example lets say D = -1,
then we have: a(n) = a(n-1) + a(n+1)
Which is just like saying: a(n) = a(n-1) - a(n-2)
But we know that a(n-1) = a(n-2) - a(n-3)
Which means: a(n) = -a(n-3)
Therefore: a(n) = a(n-6)
So the sequence will be periodic with period 6.
Looking at the model what we've got here is that each generation has a population of the last generation's birth rate. This is problematic because positive birth rates will tend to fall in this system, leading to negative populations. This then becomes periodic because a negative birth rates of negative populations will leads more fewer negative individuals, i.e. greater populations.
I'm not sure this makes any sense to be honest. I suggest abandoning the model at this point!
Anonymous
Thanks very much for your expert help. As you must have seen, the sequence I'd already come up with for D = - 1:
0 1 1 0 -1 -1 0 1 1 . . .
complies with the rule or algorithm a(n) = a(n-6) which you derive. However, the mathematical reasoning you employed to do that derivation is new to me. Is there a name for it? Where can I learn more about it?
I dimly follow your reasoning about negative birth rates. Can you think of any model other than biological reproduction to give sense to the equations?
Lastly, it looks like you could help me with another problem arising from a +plus magazine article. It's titled "When things get weird with infinite sums", Dec 18 2014. I wrote what is still the only comment under the heading "La Grandillusione", but am happy to be put right if I've failed to grasp what the Grandi series is about.
Chris G
Anonymous
At some lectures I attended perhaps 50 years ago, there was a discussion about infinities.
Am I the only person to remember all this?
The size of a countable set, was defined as “Aleph null" א subscript 0
The smallest infinity.
Because the Hebrew script is to difficult to handle in Word, I shall call it N.
The arithmetic if these infinite numbers is interesting.
If N is the size of the non-negative integers, {0,1,2,3,4,5 ...)
then, for example the set of positive and negative integers {0,+1,-1,+2,-2,+3,-3,…} is of size 2N.
and the set of positive even numbers {0,2,4,6,…} is of size ½ N.
So, in infinite arithmetic (N being Aleph Null)
N + 1 = N
N x 2 = N
then fractions, which can be defined as the ration of two integers a/b
are therefore a set of size N squared
and so
N x N (= N squared) = N
Can we find a larger number? Answer, yes.
If we move on to Real numbers, rather than rationals,
we find the set is uncountable. (Bigger than countables)
So writing the real numbers as a countably infinite decimal expansion for example,
the real number set is of size 10 tot he power N
A countable set of choices of digit.
So 2 to the power N (= 10 to the power N, etc) is bigger. We would call it Aleph 1.
I never pursued this any further.
But can we construct even bigger infinities?
Is there an Aleph 2 and an Aleph 3, even an Aleph aleph.
This is infinitely better than Googleplex!
Is there any literature that takes this further?
I would be glad to know.
Or is all this in Georg Cantor's work?
Meanwhile back to the real world (or rational ...)
Richard Billinghurst. St John's 1967. Mathematics. later theology. It is all the same! God is a mathematician.
Marius de Jess
The word/concept of limit or finity is founded on the experience of mankind.
Now, mankind has the habit of using word particles like the prefix in to make what I call artificial words, e.g. with the prefix of in added to the word finity, man comes to a new word, namely, infinity.
But no man has ever experienced an infinity at all, and it is impossible with him, no matter that the word infinity is to my insight meaningless - what is meaningful is the word fullness, as with God there is fullness of existence.
No matter how Cantor wants to be smart, he is basically just into abuse of language; for the purposes now mathematicians achieve with his abuse of language, in his smart-ass manipulation of the otherwise meaningless word infinity, those achievements can be reached even without smart-ass manipulation of the meaningless word infinity.