
Plus Advent Calendar Door #14: Euler's polyhedron formula
A polyhedron is the 3D version of a polygon. It's a solid object whose surface is made up of a number of polygonal faces. Two faces meet in an edge and the corners of a polyhedron are called vertices.
Euler's polyhedron formula, named after Leonhard Euler, is a pretty amazing equation relating the number $E$ of edges, $V$ of vertices and $F$ of faces of a polyhedron: $$ V-E+F=2 $$ As an example, think of a cube. It's got 6 faces, 8 vertices and 12 edges: $$ 8-12+6=2 $$ as required.
The amazing thing is that this formula holds for all polyhedra, except for those that have holes running through them.
Using this formula, you can figure out quickly that there is no simple polyhedron (that is one without holes) with exactly seven edges. Similarly, there is no simple polyhedron with ten faces and seventeen vertices.
The formula also makes it possible to prove one of the most beautiful results in geometry, that there are only five Platonic solids.
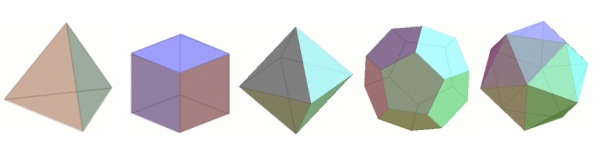
Figure 7: The Platonic solids. From left to right we have the tetrahedon with four faces, the cube with six faces, the octahedron with eight faces, the dodecahedron with twelve faces, and the icosahedron with twenty faces.
Euler's polyhedron formula applies to solids that, in a topological sense, are equivalent to the sphere: you can turn each simple polyhedron into a sphere by smoothing out the edges and corners and making it round. But you can also look at the number $V-E+F$ for polyhedra that are topologically the same as a doughnut, or a doughnut with two, three, four or any number of holes. This number is called the Euler characteristic and it turns out that it is always equal to 2 minus 2 times the number of holes. So the Euler characteristic doesn't only tell us something about polyhedra, but also something very deep about the nature of shape and space in general.
You can find out more about Euler's polyhedron formula, including a proof, in this Plus article. And there's an interesting application to designing footballs in A fly walks around a football.