
Infinite sums and China's demographics
China has just revoked its one-child policy. What better occasion to explore the mathematics of population growth with an example. You may be surprised at the result.
One child at a time
Unlike our canine friends, which regularly have litters of several puppies, we humans most often have one child at a time. Together with our relative freedom to decide when to have children, this may present families with a problem: "Should we have another child, given the number of children and the particular traits of the children we already have?" For example, families with two sons might face the dilemma that, on the one hand, three children might be excessive, but on the other, a girl would bring extra joy to the family. Of course, should a third one turn out to be yet another boy, the dilemma would simply be shifted one notch up. In any case, the expectation of a particular trait (female) might make the numbers (three or four) seem less excessive.

Humans and dogs have different breeding patterns.
But how can decisions on whether or not to continue having children, given the gender of previous children, affect the growth of populations? This question motivates the hypothetical problem in demographics that follows.
R's demand
People have the terrible habit of making decisions by themselves without concern for the needs of mathematicians. To do away with this inconvenience, we simplify matters slightly and imagine a kingdom governed by a not too malevolent Ruler (call them R) with the power to dictate how many children women can have. R finds that the kingdom has an excess of people (an excess which R is obviously not a part of), and so wants to curb population growth by restricting the number of children women can have. R knows that such a measure will not be popular — especially because people in the kingdom place great value on sons (unlike the family in the paragraph above) and would feel unhappy with only daughters. R therefore wishes to make sure that all women get a fair chance of having male progeny.
M's rule
In compliance with R's demand, the kingdom's Minister for Mathematical Problems (MMP or M in short) comes up with a simple decree: women will be allowed as many children as they want as long as they stop having children once they have a boy. Obviously, since women cannot be obliged to have children, they may have no children at all or stop at any number of daughters for whatever reason. For example, a woman would be allowed ten children if they happened to be either nine daughters first and one son last or ten daughters only. Unlike the mother of one son, however, the mother of ten daughters would be free to choose whether to have an eleventh child.
R becomes confused with M's proposal, especially when confronted with a graphic interpretation of its consequences (see the figure below). The rule seems indeed to give all women a fair chance of a son, but how does it curb population growth? After all, the first part of the rule says that women can have as many children as they want. And there's a lot of pink and very little blue in the cartoon. So, won't the rule bring about an excess of girls over boys? Here's M's explanation why it doesn't.
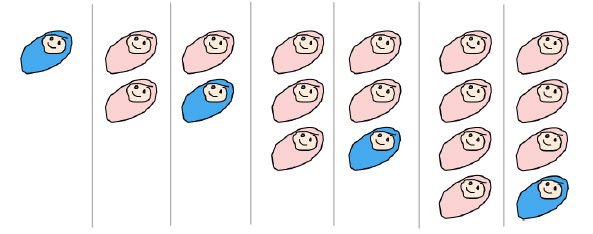
Possible sets of siblings (sibling sets are arranged vertically) under M's rule (depicted here for up to four children).
M's explanation
If women are as likely or less likely to give birth to girls as they are to give birth to boys, then the proportion of females in the initial population will be at most half. If the average number of children per woman is less than two, then the population will not grow sustainably, since not everyone in a given generation will be replaced. In fact, the probability of boys' births is slightly higher than the probability of girls' births (about 51: 49), so even an average of two children per woman is below replacement rate. M will, however, take those odds to be 50:50.

A 50:50 chance for boys or girls.
Since no woman can have more than a single boy, the average number of boys per woman cannot be greater than one and neither can the average number of girls per woman, given that the rule has no effect on gender balance. So, the average number of children per woman is at most two. But this maximum requires that all women become mothers, and that all mothers can potentially have infinitely many children and will always carry on having children until a boy is born. Since none of these can realistically be the case, the average number of children per woman will always be less than two and therefore the population won't grow.
R, however, is not convinced with this explanation and orders M to deliver proof. So, M goes on to calculate the largest possible average number of children per mother that can be reached under the rule, keeping in mind that this maximal average will always be greater than the real average number of children per woman since not all women will have children. Multiple births will be ignored because they are rare events if gender is not considered, and even rarer if narrowed down to cases of more than one boy.
Probabilities
We write $p(1),$ $p(2),$ and $p(n)$ for the probability of a mother having $1,$ $2,$ or $n$ daughters in her lifetime and $g_i$ for the probability of a mother of $i$ girls going on to have another child. Then $(1-g_i)$ is the probability of a mother of $i$ girls stopping to have children. Then \begin{eqnarray*}p(1) & = & p(\mbox{girl, stop}) &+& p(\mbox{girl, continue, boy})\\ & = & \frac{1}{2}(1-g_1) &+& \frac{1}{2} \times g_1 \times \frac{1}{2} \\ &= &\frac{1}{2}(1-g_1) &+& \frac{1}{4} g_1 \end{eqnarray*} Similarly, \begin{eqnarray*}p(2) & = & p(\mbox{girl, continue, girl, stop}) &+& p(\mbox{girl, continue, girl, continue, boy})\\ & = & \frac{1}{2} \times g_1 \times \frac{1}{2} \times (1-g_2)&+& \frac{1}{2} \times g_1 \times \frac{1}{2} \times g_2 \times \frac{1}{2} \\ &= &\frac{1}{4}g_1(1-g_2) &+& \frac{1}{8} g_1g_2. \end{eqnarray*} In general, the probability $p(n)$ of a woman having $n$ daughters is $$p(n) = \frac{1}{2^n} g_1g_2 ... g_{n-1}(1-g_n) + \frac{1}{2^{n+1}} g_1g_2 ... g_{n-1}g_n.$$ The left-hand term of this sum stands for women who have $n$ daughters and then stop, and the right-hand term stands for women who have $n$ daughters followed by a boy. Multiplying out the bracket gives \begin{eqnarray*} p(n) & =& \frac{1}{2^n} g_1g_2 ... g_{n-1} - \frac{1}{2^n} g_1g_2 ... g_{n-1}g_n + \frac{1}{2^{n+1}} g_1g_2 ... g_{n-1}g_n\\ &=&\frac{1}{2^n} g_1g_2 ... g_{n-1} - \frac{1}{2^{n+1}} g_1g_2 ... g_{n-1}g_n. \end{eqnarray*} Now let's turn to the boys, writing $q(n)$ for the probability of a woman having $n$ boys. Since women have to stop having children as soon as they have a boy, $q(n)=0$ for all $n>1.$ The probability $q(1)$ of a woman having one boy, by contrast, is made up of infinitely many terms: \begin{eqnarray*} q(1) &=& p(\mbox{boy}) &+& p(\mbox{girl, continue, boy}) &+& p(\mbox{girl, continue, girl, continue, boy})&+& ... \\ & = & \frac{1}{2} &+& \frac{1}{2} \times g_1 \times \frac{1}{2} &+& \frac{1}{2} \times g_1 \times \frac{1}{2} \times g_2 \times \frac{1}{2} &+& ... \\ & = & \frac{1}{2} &+& \frac{1}{4} g_1 &+& \frac{1}{8}g_1g_2&+& ... \end{eqnarray*} The $nth$ term in this sum is $$\frac{1}{2^n}g_1g_2 ... g_{n-1}.$$Balance of gender
The average (expected) number $s$ of sons per woman is $$s = 1 \times q(1)+2 \times q(2)+3\times q(4)+ ...,$$ which is just $q(1)$ since all other $q(n)$ are equal to zero. So we have $$s = q(1)=\frac{1}{2} +& \frac{1}{4} g_1 + \frac{1}{8} g_1g_2+ .. +\frac{1}{2^n}g_1g_2...g_{n-1}+...$$ The average number $d$ of daughters is \begin{eqnarray*} d &=& 1\times p(1) +2 \times p(2)+3 \times p(3)+ ... + n \times p(n) + ... \\ & = &\left(\frac{1}{2}-\frac{1}{4}g_1\right) + 2\left(\frac{1}{4}g_1 - \frac{1}{8}g_1g_2\right) +3\left( \frac{1}{8}g_1g_2-\frac{1}{16}g_1g_2g_3\right) + ... + n\left(\frac{1}{2^n}g_1g_2...g_{n-1}-\frac{1}{2^{n+1}}g_1g_2...g_{n-1}g_n\right)+...\end{eqnarray*} With a bit of thought, you can see that this sum simplifies to $$d = \frac{1}{2} +& \frac{1}{4} g_1 + \frac{1}{8} g_1g_2+ .. +\frac{1}{2^n}g_1g_2...g_{n-1}+... = s.$$ Thus, $d=s,$ so there will be no excess of girls.
Average number of children
We don't know the probabilities that a mother with a given number of daughters will continue to have another child — in other words, we don't know the values of the $g_i.$ However, we can calculate an upper bound for the average number of children per mother as follows: First, no mother can possibly have more than some number $m$ of children (for example, to play it safe, no woman could possibly have more than 100 children by natural means). This implies that $g_m = 0.$ The sums above now become $$s=d= \frac{1}{2} +& \frac{1}{4} g_1 + \frac{1}{8} g_1g_2+ .. +\frac{1}{2^m}g_1g_2...g_{m-1}.$$ This average depends on the values of the $g_i$, of course, but it attains its largest possible value when all the $g_i$ (for $iChina
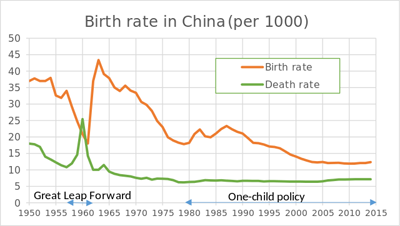
Birth and death rates in China. The one-child policy did not affect all of the population. Experts are uncertain about the extent to which the policy has reduce the birth rate. Image: Phoenix7777, CC BY-SA 4.0.
Chinese families are now allowed two children irrespective of the gender of the first child. Since not all women will have children and not all women who have a first child will go on to have a second child, the average number of children per woman will remain under two, hence below replacement rate, as with M's rule.
Further reading
Expert views on China can be found in The effects of artificial gender imbalance by Therese Hesketh and Jiang Min Min. For extensive consideration of the mathematics of demography see Applied Mathematical Demography by Nathan Keyfitz Hal Caswell.
About the author

Jorge Almeida teaches genetics at the Institute of Agronomy of the University of Lisbon, Portugal.