Probing the pint
Australians have a reputation for being fond of their beer. Some Aussie scientists from Sydney are so fond of it that they've actually solved the age-old puzzle of why the bubbles in a glass of Guinness appear to sink rather than rise.
In most situations, bubbles rise - like the bubbles in a saucepan of boiling water, or the bubbles of air breathed out by a diver.
"Everyone familiar with hydrostatics, and having even a passing acquaintance with Archimedes, knows that gas bubbles are lighter than liquid and must experience a buoyancy force driving them ever upwards until they break out of their liquid prison" said Professor Clive Fletcher from the University of New South Wales.

Flow pathlines in a glass of Guinness.
Image © Fluent Inc.
Look hard at a glass of Guinness, however, and it appears that many bubbles are moving downwards, towards the bottom of the glass. Professor Fletcher and his students set out to solve this conundrum using a fluid dynamics computer program called FLUENT and, of course, a few glasses of Guinness.
The FLUENT software took into account such factors as fluid flows, pressure, temperature and chemical concentration in different parts of the glass to examine mathematically the predicted behaviour of bubbles in the Guinness.
Professor Fletcher and his team of students from the Centre for Advanced Computational Engineering and Science discovered that the behaviour of the bubbles varies not only with the shape of the glass, but with the size of the bubbles themselves.
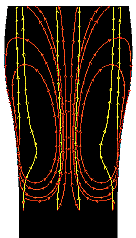
Bubble tracks show that the 1 mm bubbles (yellow) move steadily upwards while the 60 micron bubbles (red) are dragged downwards near the side of the glass.
Image © Fluent Inc.
Bubbles in the centre of the glass move upwards relatively quickly and drag liquid with them.
Now, elementary physics suggests that the overall amount of liquid in the glass must be conserved (unless somebody drinks it, of course!).
Therefore the liquid moving upwards must eventually move downwards again. The researchers found that near the walls of the glass, the liquid indeed moved downwards.
This downward-moving liquid has a dragging effect on the bubbles. Larger bubbles are more buoyant than smaller bubbles, and continue to move upwards.
Smaller bubbles (less than 0.05mm in diameter) are not buoyant enough to resist this drag force, and move downwards with the liquid near the sides of the glass. Since Guinness is rather opaque, and these downward-moving small bubbles are close to the side of the glass, it often appears that all the bubbles are moving downwards.
"From answering the perplexing Guinness riddle to helping design the escape vehicle for the International Space Station, computational fluid dynamics software is making it possible to gain a much better understanding of our environment", said Dr Keith Hanna of Fluent Inc, the company responsible for the FLUENT software.
"Of course, the primary use of our software is solving far more serious fluid flow problems - optimising vehicle aerodynamics, speeding up the mixing process in chemical reactors, improving the performance of ventilation fans, that sort of thing."
Coda: Fluid dynamics
The mathematics used to solve the problem of a pint of Guinness is the same as that used for weather forecasting - they're both fluid dynamics.
One of the interesting aspects of the flow diagrams above is the presence of eddies. These are places where the fluid recirculates - that is, it goes continuously round and round a closed curve. You can see the eddies clearly on the diagrams: first the Guinness goes up, then turns round and goes down again, then starts again.
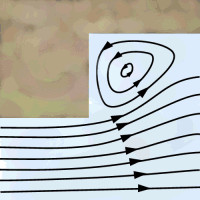
Eddies turn up in lots of other situations. If you look at a river just after a waterfall or a weir, you'll often see a region where lots of scum and rubbish accumulates. This is because the water is just recirculating there: instead of being swept away with the rest of the river-water, it simply goes round and round. Rubbish which gets into the eddy stays there because the water just moves it around.
Eddies can also often be seen in the corners of buildings during a strong wind. Just in the corner, there are often leaves whirling round and round, which mysteriously don't seem to get blown away in the wind. In fact, they're trapped in a little eddy.