Gobbling Gorillas solution

Gobbling Gorillas

A gorilla, of mass 100kg, is imprisoned inside a cage of mass 350kg, which is suspended in mid-air on a long rope thrown over a pulley. At the other end of the rope is a counterweight of mass 450kg, exactly balancing the combined weight of the cage and gorilla.

Attached to the roof of the cage, on the inside, is a delicious bunch of bananas, which the gorilla would love to eat. Unfortunately they're out of his reach, by 10cm. He decides to jump up into the air, just far enough to be able to grab the bananas, then fall back down to the cage floor.

How fast does he need to jump? Specifically, with what speed does the gorilla need to move away from the cage floor?

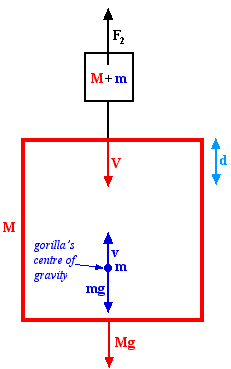
The solution

Initially, before the gorilla jumps for the bananas, everything is at rest. Considering the cage+gorilla as a system, there will be only two external forces acting on this system: the force of gravity, and the rope tension. The force of gravity is just the sum of forces from the cage and the gorilla. Let upper case letters correspond to the cage while lower case letters correspond to the gorilla. Then \[ F_1=(M+m)g \] where $g$ is the acceleration of gravity (approximately $10m/s^2$). The force of gravity acting on the counterweight must be the same as the rope tension since the cage is stationary initially: \[ F_2=(M+m)g. \] If we assume that the pulley is frictionless, and that the masses of the pulley and rope are negligible compared to the gorilla and cage, we can rearrange the system as shown on the figure. On the system as a whole, there will at all times be only two external forces acting, namely $F_1$ and $F_2$ which exactly cancel each other. Rope tensions, and forces acting on the cage from the gorilla and vice versa, can all be considered as internal forces and can thus be ignored. Due to conservation of the total momentum we therefore have \[ (2M+m)V-mv=0, \] where $V$ and $(2M+m)$ are the velocity and mass of cage+counterweight, respectively. This formula is valid at all times. After the gorilla has jumped, he is only under the influence of gravity; i.e. he has an acceleration equal to the acceleration of gravity, $g$. \par Using conservation of energy, or simply standard formulae for motion with constant acceleration, $a$, we have in general \[ h=\frac{v_f^2-v_i^2}{2a}. \] Here, $h$ is the height travelled, and $v_i$ and $v_f$ are the initial and final velocities, respectively. The gorilla grabs the bananas at zero velocity, so $v_f=0$. Furthermore, the acceleration is (including the right sign) $a=-g$. Thus, \[ h=\frac{v_i^2}{2g}. \] Using the same formula for the cage \[ H=\frac{V_i^2}{2A}. \] The initial velocity of the cage is given by the momentum conservation equation. Newton's law on the system cage+counterweight gives the acceleration \[ (M+m)g-Mg=(2M+m)A, \] which, after rearranging, yields \[ A=\frac{mg}{2M+m}. \] (Note that this could also be obtained by taking the time derivative of the momentum conservation equation.) The distance the cage has moved is thus \[ H=\frac{v_i^2m}{2g(2M+m)}. \] It suffices therefore that the sum of the distances travelled by the cage and gorilla, $d=H+h$, is the required 10cm. So \[ d=H+h=\frac{v_i^2}{2g}\left(1+\frac{m}{2M+m}\right), \] which gives in terms of $v_i$ \[ v_i=\sqrt{\frac{gd(2M+m)}{M+m}}. \] This is the velocity {\em relative to a stationary observer}. The velocity asked for is actually the velocity {\em relative to the cage}, $v_r=v+V$. Using the momentum conservation equation, we find \[ v_r=v+V=\frac{2v(M+m)}{2M+m}. \] Thus the relative velocity is \[ v_r=2\sqrt{\frac{gd(M+m)}{2M+m}}. \] This could also have been obtained by considering the relative acceleration instead of the relative velocity as we have done here. Inserting the values $g=10 {\rm m}/{\rm s}^2$, $d=0.1{\rm m}$, $M=350 {\rm kg}$, and $m=100 {\rm kg}$, we obtain the initial relative velocity: \[ v_r \mbox{ is approximately } 1.5 {\rm m}/{\rm s}. \]