
Radioactive decay and exponential laws
In his article Light Attenuation and Exponential Laws in the last issue of Plus, Ian Garbett discussed the phenomenon of light attenuation, one of the many physical phenomena in which the exponential function crops up. In this second article he describes the phenomenon of radioactive decay, which also obeys an exponential law, and explains how this information allows us to carbon-date artefacts such as the Dead Sea Scrolls.

Radioactive Decay
In the previous article, we saw that light attenuation obeys an exponential law. To show this, we needed to make one critical assumption: that for a thin enough slice of matter, the proportion of light getting through the slice was proportional to the thickness of the slice.
Exactly the same treatment can be applied to radioactive decay. However, now the "thin slice" is an interval of time, and the dependent variable is the number of radioactive atoms present, N(t).
Radioactive atoms decay randomly. If we have a sample of atoms, and we consider a time interval short enough that the population of atoms hasn't changed significantly through decay, then the proportion of atoms decaying in our short time interval will be proportional to the length of the interval. We end up with a solution known as the "Law of Radioactive Decay", which mathematically is merely the same solution that we saw in the case of light attenuation. We get an expression for the number of atoms remaining, N, as a proportion of the number of atoms N0 at time 0, in terms of time, t:
N/N0 = e-lt,
where the quantity l, known as the "radioactive decay constant", depends on the particular radioactive substance.
Again, we find a "chance" process being described by an exponential decay law. We can easily find an expression for the chance that a radioactive atom will "survive" (be an original element atom) to at least a time t. The steps are the same as in the case of photon survival.
Mean lifetime of a Radioactive Atom
On average, how much time will pass before a radioactive atom decays?
This question can be answered using a little bit of calculus. Suppose that we invert our function for N/N0 in terms of t, to get an expression for t as a function of N/N0. Once we have an expression for t, a "definite integral" will give us the mean value of t (this is how "mean value" is defined).
From the equation above, taking logarithms of both sides we see that lt = -ln(N/N0) = ln(N0/N), so our equation for t is
\[ t = t \left(\frac{N}{N_0}\right) = \frac{1}{l} \ln \left(\frac{N_0}{N}\right).\]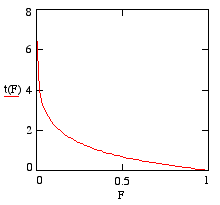
t plotted against F
For convenience, we'll now write F for N/N0. Note that that the domain of F is the interval from zero to 1, which corresponds to the interval of time from zero to infinity. Plotting t against F with a value of l=1 gives the graph on the right.
To find <t>, the mean value of time of survival, all we have to do is find the integral
\begin{eqnarray*} &= \frac{1}{1-0} \int _0^1 \frac{1}{l} \ln \frac{1}{F}dF\\ &= -\frac{1}{l}\int _0^1 \ln (F)dF\\ &= \frac{1}{l}, \end{eqnarray*}which is a very tidy result!
Incidentally, our formula for t gives us an easy way of finding the half-life, the time it takes for half the nuclei in a sample to decay. The half-life (often denoted t1/2) is just t(1/2) = (1/l) ln(2). The equivalent thickness for the medium in radiation attenuation is known as "half-value thickness". Similarly, in a population which grows exponentially with time there is the concept of "doubling time".
Libby's Legacy
We started the first article by talking about carbon dating and the Dead Sea scrolls. Let's look further at the technique behind the work that led to Libby being awarded a Nobel prize in 1960.
Carbon 14 (C-14) is a radioactive element that is found naturally, and a living organism will absorb C-14 and maintain a certain level of it in the body. This is because there is carbon dioxide (CO2) exchange in the atmosphere, which leads to constant turnover of carbon molecules within the body cells.
Once an organism dies there is no further CO2 exchange, and so the ratio of C-14 to the far more common carbon isotope, C-12, will begin to decrease as the C-14 atoms decay, yielding nitrogen (N-14) with the emission of an electron (or "beta particle") plus an anti-neutrino.
The ratio of C-14 to C-12 in the atmosphere's carbon dioxide molecules is about 1.3×10-12, and this value is assumed constant for the main part of archaeological history since the formation of the earth's atmosphere.
Knowing the level of activity of a sample of organic material enables us to deduce how much C-14 there is in the material at present. Since we also know the ratio of C-14 to C-12 originally, we can find the time that has passed since carbon exchange ceased, that is, since the organic material "died".
In the case of the Dead Sea scrolls, important questions required answers. Were they forgeries? Did they really date from around the time of Christ? Before or after?
Using Libby's radiocarbon dating technique, the scrolls have been dated, using the linen coverings the scrolls were wrapped in. One scroll, the Book of Isaiah, has been dated at 1917BC ±275 years, certainly long before the time of Christ. Some of the others are roughly contemporary with Christ.
Let's take a look at an example of how dates are calculated using Libby's method.
Suppose a linen sample of 1 gram is analysed in a counter. The activity is measured at approximately 11.9 decays per minute. We'll denote the magnitude of the rate of decay of the Carbon 14 nuclei as R. This magnitude is equal to the rate that beta particles are detected. So \[ \frac{dN}{dt} = -R.\]
Recall that the exponential law for the number of Carbon 14 nuclei present says that
\[ N = N_0 / e^{-l t}, \]and so
\[ \frac{dN}{dt} = - l N_0 / e^{-l t} = -l N,\]which tells us that R=lN, and that the activity at t=0 (the time the linen was manufactured) is R(0) = lN0.
Substituting gives us an exponential relation in terms of the measured activity: \[ R = R_0 e^{-l t}. \]
Now the decay constant for Carbon-14 is l = 3.8394 × 10-12 per second. This corresponds to a half life of 5,730 years.
We can calculate the number of Carbon-12 nuclei in 1 gram of carbon:
\[ \frac{6.02 \times 10^{-12} \mbox{ nuclei/mole}}{12.0 \mbox{ grams/mole}} \times 1 \mbox{ gram} = 5.0167 \times 10^{-22} \mbox{ nuclei}.\]Using the (living) ratio of C-14 to C-12, this implies that the original (t = 0) number of Carbon 14 nuclei was
\[ (1.3 \times 10^{-12}) \times (5.0167 \times 10^{22}) = 6.5221 \times 10^{10}.\]Now, rearranging the exponential activity law gives \[ t = -\frac{\ln(R/R_0)}{l}.\]
R0 is simply (3.8394×10-12)(6.5221×1010) = 0.2504 decays per second. The measured rate is R(t) = 11.9 decays per minute = 0.1983 decays per second.
The value for t that results is
\[ 6.0758 \times 10^{10} \times \frac{1 \mbox{ year}}{3.15\times 10^{7} \mbox{ seconds}},\]which is approximately 1929 years. This an approximate age for some of the scrolls.
In a similar way, dating charcoal found at Stonehenge gives ages of approximately 3798 ±275 years, and, when used on some of the oldest archaeological artefacts in the Americas, the technique gives ages of approximately 25,000 years, corresponding to a time of significantly lower sea levels and supporting the theory that the very first humans in the "New World" crossed the Bering Straits by foot from Siberia into Alaska.
Incidentally, other "larger time scale" radio-dating techniques exist, apart from Libby's radiocarbon method. Here isotopes with longer half lives are used, which enables dating of geological formations and rocks. However, the essential ideas are analogous. For example, in lava form, molten lead and Uranium-238 (standard isotope) are constantly mixed in a certain ratio of their natural abundance. Once solidified, the lead is "locked" in place and since the uranium decays to lead, the lead-to-uranium ratio increases with time. In this way, some of the oldest rocks have been measured at approximately 3 billion years.
About the author
 Ian Garbett lectures in applied radiation/radiological physics within the Medical Radiation Science courses at Charles Sturt University, Wagga Wagga NSWAustralia.
Ian Garbett lectures in applied radiation/radiological physics within the Medical Radiation Science courses at Charles Sturt University, Wagga Wagga NSWAustralia.
He graduated in 1977 with a BSc Honours in Applied Physics from the University of Lancaster, and obtained an MSc in Medical Physics from the University of Leeds in 1987.
He is interested in various theoretical aspects of radiation and radiological physics, with an interest in mathematical modelling in general.
Current research involves a theoretical description of X-ray beam spectra.