A Reader's Solution

The first correct solution we received for Puzzle No 8 - The Gobbling Goat was this one from V. Shashidhar.

You can see the more detailed PASS Maths solution for a step-by-step explanation of how to tackle the problem.

The answer to the question is 115.8 metres.

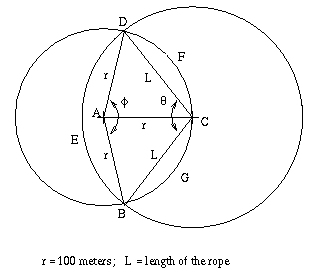
It comes as a root to the equation \begin{equation} {2r^2 \arcsin(\frac{L}{2r})} - {\frac{L}{2}\sqrt{4 r^2 - L^2}} + {L^2 \arccos(\frac{L}{2r})} = {\frac{\pi r^2}{2}} \end{equation} where $r=100$ metres and $L$ is the length of the rope used to tie the goat. \par The derivation is as follows (see figure): \begin{eqnarray*} \\ \theta &=& 2 \arccos \frac{L}{2 r} \\ \phi &=& 4 \arcsin \frac{L}{2 r} \\ Area(CDEB) &=& \frac{\theta L^2}{2} \\ Area(DCF) &=& Area(ADFC) - Area(ADC) \\ &=& {r^2 \arcsin \frac{L}{2 r}} - {\frac{L}{4} \sqrt{4 r^2 - L^2}} \\ Area(EDFCGB) &=& Area(CDEB) + 2 Area(DCF) \\ &=& \frac{\pi r^2}{2} \end{eqnarray*} This implies equation (1).