
Seeing Pythagoras
Below are three visual proofs of Pythagoras' theorem, which were sent to Plus by John Diamantopoulos, Professor of Mathematics at Northeastern State University.
The first visual proof is probably similar to the one Pythagoras himself used. Watch the animated gif to see how regions within the initial square can be rearranged to provide a proof. To replay the animated gif simply hover your mouse over the image.
Below is a video illustrating this proof. And you can play with a Geogebra applet illustrating it here.
The second visual proof is probably similar to one used by the ancient Indian mathematician Bhaskara. Again, it's a rearrangement of regions within the initial two squares that give the proof. To replay the animated gif simply hover your mouse over the image.

Below is a video illustrating this proof. And you can play with a Geogebra applet illustrating it here.
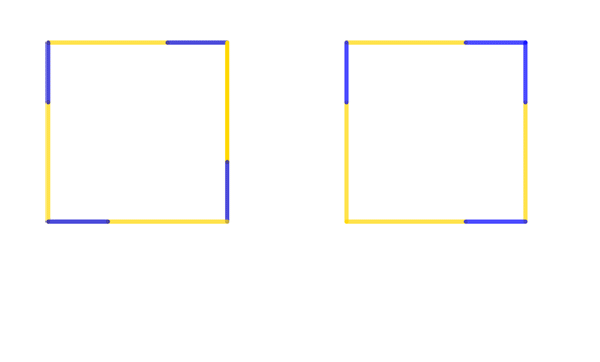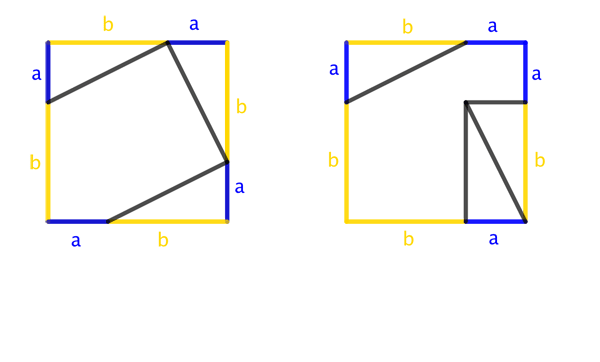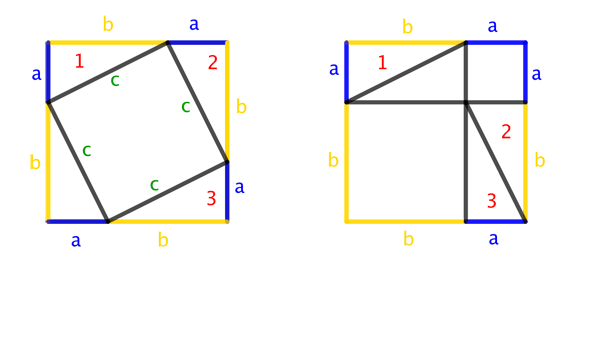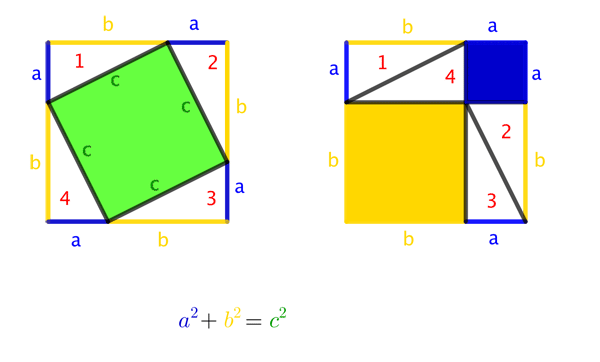
The third visual proof was originally constructed by the 20th President of the United States, James Garfield. It uses the area formula of triangles. We do wonder whether the current US president also dabbles in geometry in his spare time. To replay the animated gif simply hover your mouse over the image.

Below is a video illustrating this proof. And you can play with a Geogebra applet illustrating it here.
As you'll have noticed, the last visual proof uses the fact that $$(a+b)^2=a^2+2ab+b^2.$$ This too can be demonstrated using pictures. To replay the animated gif simply hover your mouse over the image.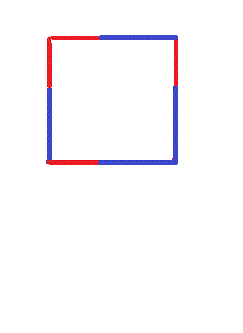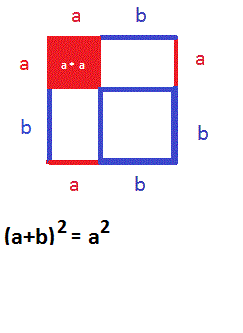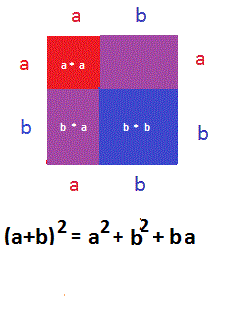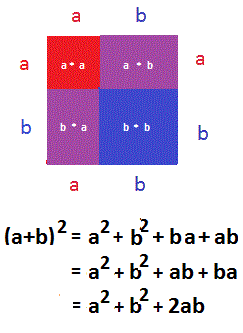
About this article

John C. D. Diamantopoulos is a Professor in the Department of Mathematics and Computer Science at Northeastern State University in Tahlequah, Oklahoma. His mathematical interests include ordinary differential equations, mathematics education and the history of mathematics. Diamantopoulos is also very active in his church, volunteering on computer productions/presentations and any area that needs attention.
This article was first published in February 2018 and updated in December 2019.