Simone Biles: Defying the laws of physics?

Simone Biles is a gymnast in a league of her own. In the 2016 Olympics in Rio she stunned audiences with a move some thought defies the laws of physics: the Biles, which incorporates a double somersault, a twist in mid-air, and a blind landing (see the video below). How does she do it? We asked sports scientist Ciarán McInerney and sports engineer John Kelley to explain the physics of the Biles.

Here are the questions we asked. Click on the links to find the answers.

How does Simone make her body spin, and control the spin, in the air?

This is all about conservation of angular momentum. We start with Newton's first law of motion: an object (or a gymnast) either remains at rest or continues to move at a constant velocity, unless acted upon by a net force. Put simply, things that are moving want to stay moving and things that are stationary don't want to move. The key terms here are momentum and inertia: momentum keep things moving, inertia is what we call a body's resistance to changing its momentum. These ideas are quite intuitive, especially when you think about your own experience of trying to stop moving things and trying to move stationary things. It's safe to say that faster things are harder to slow down and heavier things are harder to move. The formula for linear momentum (momentum of motion along a straight line) is:

\begin{equation}\rho=mv.\end{equation} Here $\rho$ is linear momentum, $m$ is the mass of the object (the gymnast) and$v$ is its velocity. For angular momentum (momentum of circular motion) $L$ we replace mass with the mass moment of inertia $I$ and linear velocity with angular velocity $\omega$: \begin{equation}L=I\omega.\end{equation} Angular velocity is simply the rotational equivalent of velocity. A body's mass moment of inertia, $I$, is an indication of its resistance to a change in its rotation. Think of it like this: the more mass something has, the heavier it is, and heavier things are harder to move than lighter things. Heavier things are also harder to rotate. Additionally, longer things are harder to rotate than shorter things. Mass moment of inertia is a single characteristic that captures a body's resistance to rotation based on its mass and shape.

This reflects our experiences because it says that heavier and faster things have more momentum than lighter and slower things. But how does this relate to somersaults and twists?

The law of conservation of angular momentum can be defined in many ways but the gist is that that angular momentum of a body will stay constant provided that it is not acted upon by external forces. For Simone, this means that the momentum that she has when she takes off is all the momentum that she can use for her aerial acrobatics.

You can see the movements described in the text in the video.

Let's say that I am a gymnast and I need $L$ angular momentum to complete one stretched somersault. If I wanted to do two somersaults with the same angular momentum, then I would need to spin faster. Angular velocity, $\omega$, is a measure of my spin. According to equation 2, I will need to decrease my mass moment of inertia, $I$, in order increase my angular velocity because my momentum, $L$, stays constant. How do I do that? Well, just like heavier things are harder to move than lighter things, longer things are harder to rotate than shorter things. By tucking into a ball that is half the length of my outstretched body, I might be able to make it around twice and complete my double somersault.

Simone has oodles of momentum going into her double stretched somersault but she still makes use of the conservation of angular momentum. If you watch her perform the skill, you might be able to notice the two ways that Simone decreases her mass moment of inertia in order to somersault faster. The first is that she pulls herself into an arch. The length between the end points of an arch is always shorter than the length of body that is arching. This does a little but not much. The bigger contributor is when she snaps her arms to her hips just after her first quarter somersault. By snapping her arms down to her hips she now measures from head-to-toe rather than fingers-to-toes. This is a big change in length.

Let's talk about twisting. It seems like out of nowhere, Simone suddenly twists at the end of her double stretched somersault. She takes advantage of a handy characteristic of the conservation of angular momentum: momentum is conserved across all axes. This means that Simone can take momentum from her somersaulting axis and transfer it to her twisting axis. She does this by changing the shape of her body and causing a tilt.

Tilting takes momentum. If Simone tilts during a somersault she must borrow momentum from one of the other axes because the momentum was fixed at take-off. Perhaps she borrowed it from her somersault, but that would slow her somersaulting down – dangerous move. The other option is to borrow it from her twisting axis. But how can she take angular momentum from her twisting axis if she isn't twisting? She goes into negative twisting. Positive and negative are just opposite directions. A negative twist is just a twist in a different direction to a positive twist. When she tilts, she borrows momentum from her twisting axis so she starts to twist negatively. To stop a twist, she un-tilts, which returns the twisting momentum back to zero.

How does she do it? Image: Agência Brasil Fotografias, CC BY 2.0.

So, how does she tilt? The answer is asymmetric arm movement. If you hold one arm out to the side you will tilt ever so slightly (hold a weight to feel a bigger tilt). Hopefully, your centre of gravity will stay over your base of support and you won't fall over. As Simone enters her second somersault, you'll see her pull her left arm inward to her belly button. Just like our standing experiment, she has moved one arm so that she will slightly tilt. This little tilt is sufficient for the half-twist that she needs.

The interesting thing about twisting is that somersaults naturally want to twist. Gymnasts put a lot of effort into not twisting. The first reason is that real-life somersaults are not likely to take off perfectly so some force will be off-axis and cause a turning effect. Another reason is the phenomenon of nutation. In short, the axis of a rotating body wobbles. If Simone kept somersaulting forever you'd see that she would be tilting left and right and she spun. Practically, this means that the gymnast is actually forced into tilting simply because they are somersaulting.

Back to the list of questions.

Where does Simone's energy come from?

To answer this question we need the law of conservation of energy, Newton's third law of motion and Hooke's law. The law of conservation of energy says that energy cannot be created or destroyed. In Simone's case, she converts the energy that she built during her run into the energy needed to perform her tumble. All she is doing is redirecting her horizontal energy from her sprint, and the vertical and rotational energy from her flic. All of this kinetic energy comes from chemical energy released within her muscles, but that is a conversation for another day. It should be noted that Simone's short stature means that she can include more steps in her run-up than a taller gymnast. Each of these steps adds more and more energy.

Isaac Newton isn't famous for his somersaults, but he did come up with the laws of motion.

Now, Newton's third law: when one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body. If this wasn't true, then the weight of your body pushing down on Earth would drill you right through it. After her run, Simone performs a round-off to turn around and a flic to convert linear energy into rotational energy. When Simone pushes into the sprung floor, it is the floor's equal and opposite force that shoots her up, not her muscular force. This might sound weird but try an experiment next time you are in a swimming pool: while floating, try to jump out of the water. You can use all the muscles in your body to mimic a jumping movement but you won't leap up like a dolphin. This is because you are pushing against the water and the water isn't as good as a sprung floor at pushing back on you. The sprung floor can't move anywhere so it directs the force back at you. The water is free to flow around the pool so it isn't so concerned with giving you porpoise performance powers.

The sprung floor is key to gymnasts' energy and protection. If they were tumbling on a hard surface like concrete, then the force that they drive into the ground would be shot back at them so quickly that it could be too much for the gymnast to handle. The Gymnova floor that Simone tumbles on is a layer of carpeted foam, on a layer of plywood that is support by an array of springs. These layers lengthen the duration of the impact, which means that the total force exerted on Simone is spread over a longer time. Newton's second law of motion tells us that:

$$F=ma,$$ where $F$ is a force, $m$ is the mass of the object experiencing the force, and $a$ is the acceleration the object experiences due to the force. We can work out Simone's acceleration as $$a=\frac{v-u}{\Delta t_{take-off}},$$ where $u$ is Simone's initial speed on making contact with the floor, $v$ is her final speed after the impact and $\Delta t$ is the time it takes to make contact with the floor. Plugging this into the equation above gives $$F=m\frac{v-u}{\Delta t_{take-off}}.$$ The equation tells us that the force $F$ is proportional to $$\frac{1}{\Delta t_{take-off}},$$ in other words, as the duration of impact increases, the force per unit time must decrease. But, of course, gymnasts don't want their force to be wasted, and it isn't. The force that Simone exerts on the sprung floor is stored as potential energy, $E_p$, within the compliant elements of the floor: $$E_p = \frac{1}{2}kx^2.$$ This is Hooke's law: $k$ is the spring constant, which measures the stiffness and strength of the spring (in this case the sprung floor), and $x$ is the how far the spring is displaced by the impact. During the short time that Simone is in contact with the floor, there will come a point where the energy she is putting into the floor will be less than the energy that the floor is storing. At this point, the sprung floor will start to give Simone her energy back and rocket her up into the air.

Back to the list of questions.

What is the energy Simone needs for the move?

The answer is around 1560 Joules. With this much kinetic energy you could throw a tennis ball straight up at 857 km/h and it would reach a height of almost 3 km (assuming no air resistance). It takes a bit of a calculation to work out her energy, but it's well worth the effort.

\setcounter{equation}{2} To perform the Biles, Simone needs to travel through the air and spin. Her kinetic energy on take-off, $E_{k \; take-off}$, therefore needs to incorporate two elements: $E_{k \; linear}$, the kinetic energy required for travelling, and $E_{k \; rotational}$, the kinetic energy required for spinning. This gives the equation \begin{equation}E_{k \; take-off} = E_{k \; linear} + E_{k \;rotational}.\end{equation} We can break this equation down further by considering that she moves up and forward. This means that her linear energy decomposes into a vertical and a horizontal component: \begin{equation}E_{k \; take-off} = E_{k \; vertical} + E_{k \; horizontal} + E_{k \;rotational}.\end{equation} To simplify the problem, we assume that the gymnast is a point mass, that is, that she is just a point particle. If you wanted to do a more accurate job, you could model each segment of the gymnast separately and combine the values appropriately in a global reference frame (see the figure below).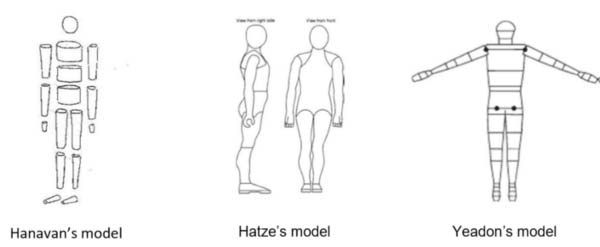

Models of body segmentation. Images taken from this paper by Laura-Anne Furlong, CC BY-NC-ND 4.0.

\setcounter{equation}{4} Kinetic energy is dependent on the speed $v$ and the mass $m$ of a body: \begin{equation}E_{k \; linear} = \frac{1}{2}mv^2.\end{equation} Equation 5 works for linear energy and we will use that equation to calculate $E_{k \; vertical}$ and $E_{k \; horizontal}$.

Biles at the 2016 Olympics. Image: Agência Brasil Fotografias, CC BY 2.0.

\setcounter{equation}{5} In the Biles there are two rotations about Simone's somersaulting axis and a half rotation about her twisting axis. A distinction needs to be made between these rotations. The somersaults occur throughout the flight phase but the twist only occurs in the final quarter of the flight phase. The equations that we have discussed so far assume constant motion. They can be applied to Simone's somersaults and her vertical and horizontal travel. From this, we calculate $E_{k \; take-off}.$ The twist, however, is not constant — she only twists at the end. The energy required to cause a twist that is not constant over the flight phase must come from work done by Simone during the skill. Practically, this means that when we talk about the twist in the Biles, we won't consider the entire flight phase of the skill — just the final quarter. We now have a new structure to our main equation (equation 4): \begin{equation}E_{k \; total} = E_{k \; take-off} + E_{k \; twist} = (E_{k \; vertical} + E_{k \; horizontal} + E_{k \; somersault}) + E_{k \; twist}.\end{equation} To figure out the rotational equivalent of the linear energy equations, we replace mass with the mass moment of inertia $I$ (see above) and linear velocity with angular velocity $\omega$: \begin{equation}E_{k \; rotational} = \frac{1}{2}I\omega^2.\end{equation} As we said above, mass moment of inertia is a single characteristic that captures a body's resistance to rotation based on its mass and shape. You might already have noticed that a body will have a different moment of inertia depending on the axis about which it is rotated. For example, it is easier to twist a brush handle than it is to swing it. To give a mathematical example, the mass moment of inertia for a cylinder with mass $m=2 kg$, length $l=2 m$ and radius $r=0.02 m$, rotating it as a baton twirler might, end over end, is \begin{equation}I = \frac{m(3r^2+l^2)}{12} = \frac{2(3(0.02)^2+(2)^2)}{12} = 0.6669 kg \cdot m^2\end{equation} But when spinning the cylinder around its radius, as you might a spinning top, it is \begin{equation}I = \frac{mr^2}{2} = \frac{(2)(0.02)^2}{2} = 0.0004 kg \cdot m^2.\end{equation} For linear motion we simplified the gymnast as a point mass for linear equations. We will also simplify the gymnast's shape for rotational equations. Let's represent a somersaulting gymnast as a cylinder because it's a simple shape that approximates a standing human. Even though Simone's mass, $m$, is the same for the linear kinetic energies, her mass moment of inertia will be different for her somersaulting and her twisting. Her mass moment of inertia for somersaulting, $I_{somersault}$, is calculated using equation 8 and for twisting, $I_{twist}$, using equation 9. Her somersaulting energy thus becomes: \begin{eqnarray} E_{k \; somersault} & = & \frac{1}{2}I_{somersault}\omega_{somersault}^2 \\ & = & \frac{1}{2}\left(\frac{m(3r^2+l^2)}{12}\right) \omega^2_{somersault} \nonumber \\ & = & \frac{1}{2}\frac{(3r^2+l^2)m \omega^2_{somersault} }{12}.\nonumber \end{eqnarray} And her twisting energy becomes \begin{eqnarray} E_{k \; twist} & = & \frac{1}{2}I_{twist}\omega_{twist}^2 \\ & = & \frac{1}{2}\left(\frac{mr^2}{2}\right) \omega^2_{twist} \nonumber \\ & = & \frac{1}{2}\frac{m r^2 \omega^2_{twist} }{2}.\nonumber \end{eqnarray} When we plug these equations into the equation for total energy, equation 6, we get \begin{equation} E_{k \; total} = \frac{1}{2}mv^2_{vertical} + \frac{1}{2}mv^2_{horizontal} +\frac{1}{2}\frac{(3r^2+l^2)m\omega^2_{somersault}}{12}+\frac{1}{2}\frac{mr^2\omega^2_{twist}}{2}.\end{equation} With some tidying up, we get: \begin{equation} E_{k \; total} = \frac{m}{2}\left(v^2_{vertical}+v^2_{horizontal}+ \frac{(3r^2+l^2)\omega^2_{somersault}}{12}+\frac{r^2\omega^2_{twist}}{2}\right).\end{equation} Now we have the job of estimating the values of the terms. From a quick internet search, we estimate Simone's height and mass to be $l= 1.47 m$ (height) and $m= 47 kg$ (mass). We use the distance from her spine to her shoulder to represent her radius, approximately $r= 0.25 cm$. For the velocities, we can use the equations of constant motion to help us out. For the vertical velocity, $v_{vertical}$, we can use the equation: \begin{equation} v_{vert \; final} = v_{vert \; initial} + at,\end{equation} Where $v_{vert\; final}$ is her speed at the instant before the end of flight, $v_{vert \; initial}$ is her speed at the moment of take-off, $a$ is the acceleration that she experiences and $t$ is the duration of flight. We want Simone's energy at the start of the tumble so we need to rearrange equation 12 to make $v_{vert \; initial}$ the subject of the equation: \begin{equation} v_{vert \; initial} = v_{vert \; final} - at.\end{equation} What terms do we know in equation 15? From looking at her performance, she seems to be in the air for about one second so we'll say that $t= 1 s$. The value of $a$ is $-9.812 m·s^{-2}$ because this is the value for acceleration due to gravity (we are assuming that 'up' is a positive direction and 'down' is negative). Once Simone is in flight, there are no other forces acting on her and thus, no other accelerations (we are ignoring air resistance). How to we estimate $v_{vert\; final}$? This is where we have to be a bit clever. Instead of modelling the entire flight phase, we can model just the first half. This is a good idea because we know that her vertical velocity is zero at the middle of the flight because that is the highest point of the flight – what goes up must come down, but it has to stop first. So, if we model half of the flight, then $a$ stays the same, $t$ is halved ($t= 0.5 s$) and $v_{vert \; final}= 0 m·s^{-1}$. Plugging these into equation 15 gives \begin{equation} v_{vert \; initial} =0 - (-9.812 \times 0.5) ,\end{equation} which gives $$v_{vert \; initial} = 4.9 m \cdot s^{-1}.$$ To figure out what $v_{horizontal}$ is, we can use an even simpler equation: \begin{equation} speed = \frac{distance}{time}.\end{equation} We can do this because there are no horizontal forces acting on Simone when she is in flight (again, ignoring air resistance). With no forces, there are no accelerations. From viewing her performance, it looks like she travels a horizontal distance of about $distance_{horiz}= 3 m$ (the diagonal of the floor is $16.9 m$). We said before that she is in the air for about one second, $t= 1 s$. The horizontal speed at which she must travel is therefore \begin{equation} speed_{horiz} = \frac{3}{1}.\end{equation} This is her initial horizontal velocity $v_{horiz \; initial}$, so \begin{equation}v_{horiz \; initial} = 3 m \cdot s^{-1}.\end{equation} We now have everything we need except the rotational velocities, more commonly known as angular velocities. Simone somersaults twice within $t= 1 s$, in other words, she makes two 360 degree turns in one second. This gives $$\omega_{somersault} = \frac{2 \times 360}{1} = 720^{\circ} \cdot s^{-1}$$ Translating from degrees into radians gives $$\omega_{somersault} = 4 \pi rad \cdot s^{-1}.$$ We said earlier that we would consider her twist only in the final portion of the skill. She twists half a turn in the final quarter of the skill, so $$\omega_{twist} = \frac{0.5 \times 360}{0.25} = 720^{\circ} \cdot s^{-1}.$$ In radians we get $$\omega_{twist} = 4 \pi rad \cdot s^{-1}.$$ We now have everything we need so we just put the values into equation 15: \begin{equation}E_{k \; total} = \frac{47}{2}\left(4.9^2 + 3^3+\left(\frac{(3(0.25^2)+(1.47^2)(4\pi)^2}{12}\right) + \left(\frac{(0.25^2)(4\pi)^2}{2}\right)\right).\end{equation} Working this out gives \begin{equation}E_{k \; total} = 1560.32 \; Joules.\end{equation}

Back to the list of questions.

What force does Simone experience on landing?

The answer is more force than is in the bite of an adult American alligator. Here is how we worked this out.

\setcounter{equation}{21} Simone's landing takes about $0.2$ seconds, so we set $\Delta t_{land}= 0.2 s$, during which time her velocities return to zero. From Newton's second law of motion, we know \begin{equation}F=ma=m\left(\frac{v_{final}-v_{initial}}{\Delta t_{land}}\right),\end{equation} where $F$ is a force, $m$ is the mass of the object and $a$ is the acceleration affecting the mass, due to the force $F$. To calculate the force required to stop Simone's horizontal and vertical velocities in $\Delta t_{land}= 0.2$ seconds, we will first combine Simone's horizontal and vertical velocities into a resultant velocity. This is done using Pythagoras’ theorem: \begin{equation}v_{initial \; resultant} = \sqrt{v_{vert \; initial}^2 + v_{horiz \; initial}^2}.\end{equation} Using the values for $v_{vert \; initial}$ and $v_{horiz \; initial}$ we worked out above, this gives \begin{equation}v_{initial \; resultant} = \sqrt{4.9^2+3^2} = \sqrt{33.01} = 5.75 m \cdot s^{-1}.\end{equation} Since the final horizontal and vertical velocities will be zero , $v_{final\; resultant}=0$. Therefore, \begin{equation}F = 47\left(\frac{0-5.75}{0.2}\right) = -1351.25 N,\end{equation} where $N$ denotes Newton, the unit we use to measure force. That is more force than the bite of an adult American alligator. The force is negative because it is a retarding force, ie one that is stopping Simone. The force is equivalent to almost three times her body weight. Of course, this calculation does not take into account the forces required to stop her rotations.

Back to the list of questions.

Is there a role for a sports scientist to analyse athletes' moves and use physics to suggest improvements?

Biles on the 2016 Olympics all-around gold medal podium.

Gymnasts are certainly aware of how the orientation of their limbs effects their performance, but they might not use the jargon that I have. From my coaching experience I have found that explaining the underlying physics can be useful for demystifying difficult skills and breaking them down into a manageable sequence of actions. Sometimes, gymnasts just want to know what to do rather than understand why. Studying these things is good though because it means that we can model performance and suggest what is possible but still undone. This idea is especially true in for the kind of tactical modelling done in well-defined events like track cycling, where models take physiological, biomechanical, atmospheric, and mechanical inputs into account. In gymnastics, people like Maurice "Fred" Yeadon have modelled somersaults extensively and concluded that a triple layout somersault is not likely to be possible on current spring floors given the required energy from the gymnast. That said, such energies are possible on a tumbling track and the triple layout is a relatively new skill that was forever thought to be impossible.

Back to the list of questions.

About the authors

Ciarán McInerney is a sports scientist completing a PhD at Sheffield Hallam University. He has been involved in gymnastics since the age of 7, training, competing and coaching.

John Kelley is a sports engineer in the Centre for Sports Engineering Research (CSER) specialising in video collection and analysis techniques and performance analysis software tools.