Solution to Puzzle No. 1 - the ring

For the question see "Puzzle No. 1 - the ring", in issue 1.

Most people's reaction on first hearing this problem is on the lines of "How can I possibly find the volume when you haven't told me the radius of the original sphere or the diameter of the hole?" The trick in this question is the last sentence in the statement of the problem, which said "You are told that you have enough information to solve this problem". In other words, the answer cannot depend on the sphere's radius or the diameter of the hole. Any values will do, consistent with the given height. With this insight, the solution can be stated as follows:

Solution

You are told you have enough information to find the volume, so it must be independent of the diameter of the hole - so let's make it zero. Then, since the radius of the sphere is 1 cm, the volume is

Proof

The following proof is based on the solution provided by Roger Stratford. To see that the volume of the ring depends only on the height of the ring, we need to use calculus and integration. The mathematics that follows is usually covered in the first year of a typical mathematics A-Level course.

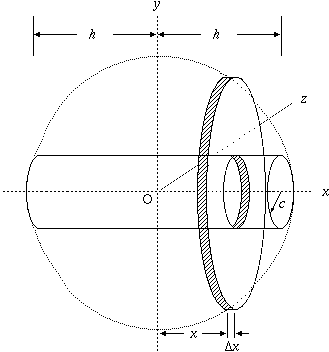
Let the total height of the ring be 2h. Consider the shape tilted so that the axis of the hole is horizontal. Take an origin at the centre of the sphere, with the x-axis along the axis of the cylindrical hole. The x-coordinate at one end of the hole is x = h, and at the other, x = -h. Let the radius of the sphere be r, and the radius of the hole be c.

Consider the ring to be made up of thin slices as shown. The outer radius of each slice is y, and the inner radius is c. The volume of each slice is

The area of the slice is the area of a circle radius y with the area of a circle radius c subtracted. Then the volume of the slice is obtained by multiplying by the thickness.

The slices run over values of x from -h to +h and so the total volume V is:

The solid is symmetrical about the OYZ plane through the origin, and so:

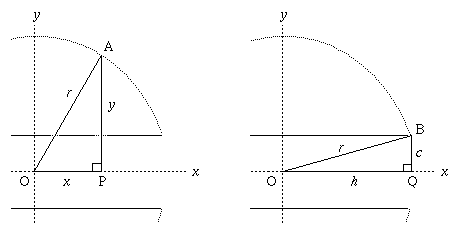
Now the section through the ring in the z = 0 plane is a circle (apart from the missing pieces). On the remaining surfaces,

(because OAP is a right angled triangle) and therefore:

By considering a point on the surface at the edge of the hole, where x = h, we have

(because OQB is a right angled triangle).

Combining (4) and (5),

and equation (3) becomes

This is a straightforward basic definite integral, which gives:

We see that this result only depends on the height of the ring.