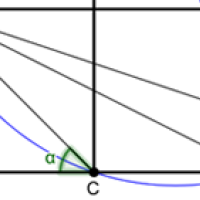
Some lovely proofs by picture
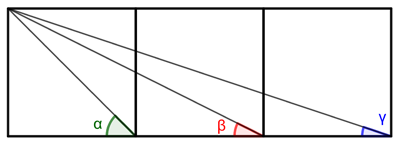
Figure1: The three angles marked add up to a right angle.
You can prove this result using the addition formulas of trigonometric functions (see here). But if you don't know these formulas, or are no good at remembering them, then that approach isn't very helpful. So let's look at some other ways of proving the result, which only require some basic geometry.
Proof by picture: Proof 1
For this method of proof first draw another row of three squares on top of the original ones, giving six squares in total. Then draw two auxiliary lines, as shown in green in the diagram below.
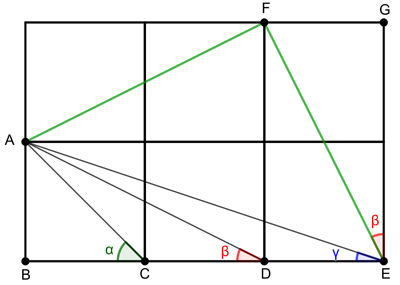
Figure 2: The two red angles are the same.
Now label some of the corners A to F as shown in the diagram. Look at the triangles ADB and FEG. Both are the result of forming a rectangle from two of the squares and slicing it in half with a diagonal line. This means that triangles ADB and FEG are congruent. And since they are congruent, the angle at the point D, $\beta$, is the same as the red angle at the point E, as shown in the diagram.
The triangle FAE is isosceles: the two green lines are both diagonals of a rectangle formed by two of the squares and therefore have the same length. The triangle FAE also has a right angle at the corner point F. You can see this by noting that the two angles making up this angle (each formed by a green and a black like) are the same two angles that make up the corner of one of the original squares, which is of course ninety degrees.
The triangle ABC is also an isosceles triangle with a right angle at one corner. This means that the two triangles ABC and FAE are similar, so the angle at the point C, $\alpha$, is the same as the angle marked green at point E, as shown below.
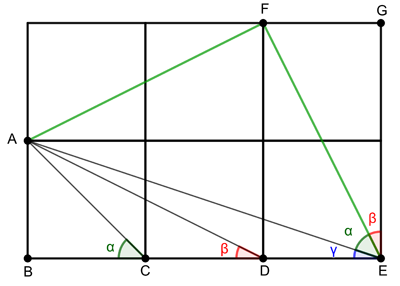
Figure 3: Label some of the corners.
Thus, the three angles we have marked at corner E are $\alpha$, $\beta$, and $\gamma$, and together they make up a right angle, as claimed.
Proof by picture: Proof 2
For the next proof, add two squares to the figure, as shown in purple below. Each of these new squares has as its diagonal the sides of two of the three original squares. It's quite easy to see that the triangle FEH and the triangle ACB are congruent, so the angle at the point C, $\alpha$, is the same as the angle marked in green at E.
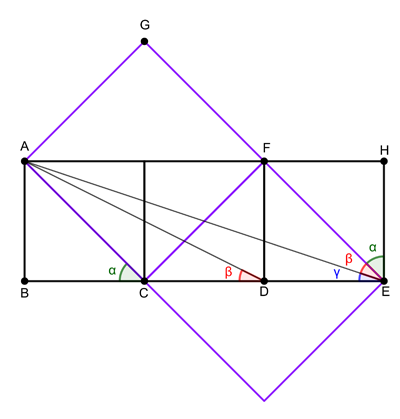
Figure 4
Now look at the triangle ADB. It's what you get when you slice in half the rectangle formed by two of the original squares with a diagonal. The triangle AEG, also comes from slicing a rectangle formed from two squares in half with a diagonal, only in this case the squares in question are the two larger ones we have just added to the diagram. Either way, this means that the triangles ADB and AEG are similar, so the angle at D, $\beta$, is the same as the angle marked in red at E.
Thus, the three angles we have marked at corner E are $\alpha$, $\beta$, and $\gamma$, and together they make up a right angle, as claimed.
Proof by picture: Proof 3
For the third proof add another row of three squares on top, so we now have nine squares in total. The middle column of squares forms a rectangle: add a diagonal of this rectangle to the figure as shown. Then draw a circle whose diameter is that diagonal.
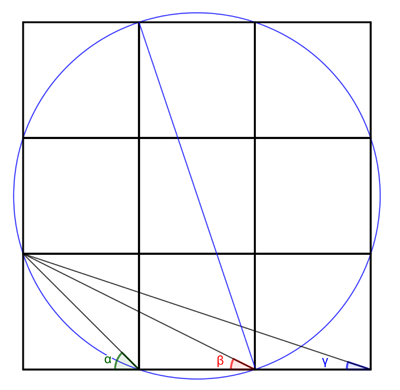
Figure 5: Draw a row of extra squares and an auxiliary line and circle.
Label some of the corners of the squares as shown in the diagram below. The triangle DFC and the triangle AEB are congruent. That's because each comes from slicing in half the rectangle formed from three squares. This means that the angle at E, $\gamma$, is the same as the angle marked in blue at F.
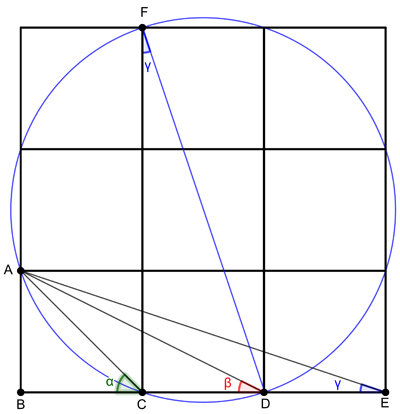
Figure 6: The blue angle at F is the same as the blue angle at E.
Next we will use one of the eight circle theorems. Imagine two points, C and D, on a circle. They cut the circle into a larger arc (around the top) and a smaller arc (around the bottom, shown red below). Now imagine picking a point X on the larger arc. Then the angle formed by the line from C to X and the line from D to X is the same, no matter where on the larger arc X lies. You can see this in the Geogebra interactivity below. You can move the point X, to see that the angle in question stays the same. You can also move C and D to see that this fact does not depend on the location of C and D on the circle.
The circle theorem applies to the points C and D in figure 6 above. This means that the angle $\gamma$, at F is the same as the angle marked in blue at A.
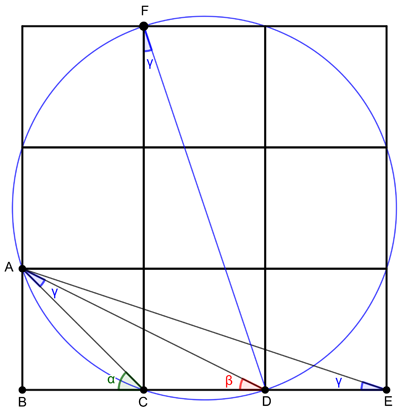
Figure 7: The blue angle at A is the same as the blue angle at E.
Finally, focus on the triangle ACD. The angle $\alpha$ is what is called an exterior angle of this triangle - it is formed by an extension of the side CD and an adjacent side of the triangle. The exterior angle theorem says that such an exterior angle is equal to the sum of the two interior angles that are not adjacent to the exterior angle. This means that $$\beta+\gamma=\alpha.$$ Now since the angle $\alpha$ is formed by the diagonal of a square and one of its sides, we have $\alpha=45^\circ$. We therefore have $$\alpha+\beta+\gamma=2\alpha=90^\circ,$$ as required.
We hope you enjoyed these three elegant proofs of our result. They aren't the only ones that don't use trigonometry. See if you can come up with others by yourself!
About the author

Yutaka Nishiyama is a professor emeritus at Osaka University of Economics, Japan. After studying mathematics at the University of Kyoto he went on to work for IBM Japan for 14 years. He is interested in the mathematics that occurs in daily life, and has written ten books about the subject. The most recent one is The Mysterious Number 6174: One of 30 mathematical topics in daily life, published by Gendai Sugakusha in July 2013 (ISBN978-4-7687-6174-8). You can visit his website here.
Comments
Stephen Fratini
Nice article ...
Noticed a minor typo, i.e., change "by a green an a black like" to "by a green and a black line"
Rachel
Thanks for spotting that!