It's the last set of the London 2012 singles final. Andy Murray steps up to the baseline to deliver the opening serve. After a few calculations he tosses the ball in the air with supreme confidence. He has maths on his side and it has given him the secret to the perfect serve...

Ok – it might be a little far-fetched to imagine the Olympic tennis champions performing calculations on the baseline but Nick Ovenden, a mathematician from University College London, has. "A fast serve can be an extremely effective weapon in tennis," says Ovenden. But no matter how fast you serve, you'll give your opponent a chance to adapt if you repeat the same serve each time. "The perfect tennis serve relies on keeping your opponent guessing about how the ball may bounce out of the service box – this can be achieved by putting spin on the ball."

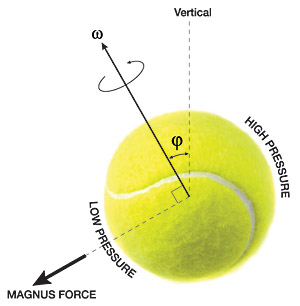
Figure 1: The spinning of a tennis ball as it flies through the air (the ball is moving into the page and spinning around an axis at an angle of $\phi$ from vertical with an angular momentum of $\omega$ radians per second) causes a difference in air pressure between one side of the ball and another – the Magnus effect

Ovenden worked with Acer and Intel to mathematically analyse the delicate balance of forces involved in a tennis serve as part of a series of activities to celebrate the launch of the new Acer Intel Ultrabook series. His analysis includes the three forces acting on a tennis ball as it flies through the air: gravity, aerodynamic drag, and something called the Magnus effect which results from the ball's spin.

The Magnus effect comes from the ball spinning as it moves through the fluid (the air). "The fluid near the ball's surface that is travelling towards the flow will be impeded and thus slows down, increasing fluid pressure," says Ovenden. "In contrast, the fluid near the opposite surface of the ball that is travelling away from the flow will be speeded up lowering fluid pressure locally. The pressure difference across the ball then leads to a net force that curves the ball towards the low pressure side."

A slice serve happens when the player hits the ball so that it spins like a top ($\phi=0$ in figure 1). This causes the ball to curve from right to left in the air as it crosses the court. "If you are going to put slice spin on the ball then naturally the ball must start travelling in a direction to the right of the straight line [to your intended target] so it can curve back."

Ovenden has calculated that the angle of deviation, $\theta$ in Figure 2 below, from the straight line to your intended impact spot, is $$ \theta = - \frac{A\omega_s}{Bu} $$ where $\omega_s$ is the vertical angular velocity (how fast the ball spins, measured in radians per second), $u$ is the balls initial speed as it leaves the racket, and $A$ and $B$ are constants that depend on the drag coefficient of the air and the straightline distance from the player to the impact point. As you'd expect, this slice constraint balances how far the slice spin moves the ball to the left with how far to the right the ball would hit if it was travelling in a straight line at an angle of $\theta$: the greater the slice spin the wider the angle.

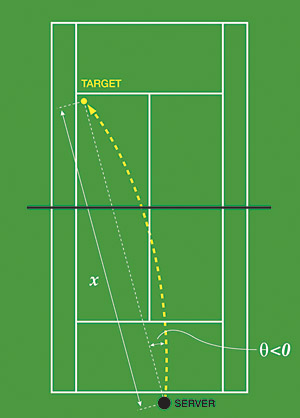
Figure 2: A slice serve occurs when the ball is hit with side spin, causing the ball to curve to one side.

The player can also put top spin on their serve, by brushing their racket up the back and over the top of the ball as it leaves the racket ($\phi = 90^{\circ}$ in the figure 1). "This leads to a negative lift force (or larger pull downwards) which makes the ball loop down towards the ground at a steeper angle," says Ovenden. "The steeper angle makes the bounce higher and wilder (kick) making it difficult to return." Ovenden has calculated that any serve has to satisfy this top spin constraint: $$ u^2(B\alpha +C) - Au\omega_t = D $$ where $\omega_t$ is the horizontal angular velocity, $u$ the ball's initial speed and $\alpha$ is the angle of elevation of the ball's path (from horizontal) as it initially leaves the racket. The constants $B$ (which also appears in the previous equation for $\theta$), $C$ and $D$ depend on the air drag and the distance to the impact point, and the constant $B$ also takes into account the height of the player while $D$ also depends on the effects of gravity. The top spin constraint balances the extra downward force from the top spin, $\omega_t$, with the speed and angle of elevation in order to make sure the serve hits the intended target: add top spin (increase $\omega_t$) and you have to hit ball faster (increase $u$) or aim higher (increase the angle of elevation $\alpha$).

In fact, introduce too much top spin and you are much more likely to hit the net. To ensure you don't score a net fault Ovendon has calculated a constraint that echoes the constraint for top spin. In order to clear the net your serve must satisfy: $$ u^2(\alpha B_n +C_n) -A_nu\omega_t > D_n $$ where the constants $A_n, B_n, C_n$ and $D_n$ are all of the same form as the constants in the above equations, but have values depending on the distance to, and height of, the net at the point the ball crosses.

The combination of slice spin and top spin makes the ball's path and bounce far harder to predict for your opponent. And varying these with each serve could be the winning formula, as long as you satisfy these three important constraints. Perhaps there's still time for Murray's coach to include some maths in his preparations for the match today...