Why is there no Gömböc in two dimensions?

Here's an argument to show why there is no convex and homogeneous two-dimensional shape with one stable and one unstable point of equilibrium.

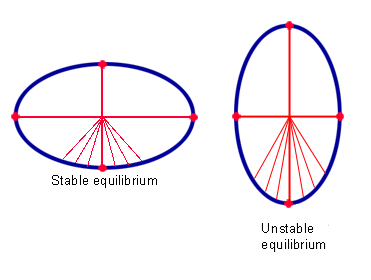
The centre of gravity G of an ellipse is the intersection of its two axes. A stable equilibrium point is closer to G than the boundary points close to it. An unstable equilibrium point is further away from G than the boundary points close to it.

Imagine a two-dimensional shape trapped between two glass plates and balancing in the vertical at an equilibrium point. You'll know from experience that the type of equilibrium — stable or unstable — is related to the location of the shape's centre of gravity. The higher the centre of gravity, the broader the "base" of the shape needs to be for the equilibrium to be stable. Mathematically this is reflected in the fact that stable equilibrium points are exactly those points on the boundary of the shape that are closer to the centre of gravity than all the boundary points in their immediate vicinity. Something similar goes for unstable equilibrium points: they are exactly those points on the boundary of the shape that are further from the centre of gravity than their immediate neighbours on the boundary. To put it formally, at a stable equilibrium the function measuring the distance to the centre of gravity has a local minimum and at an unstable point it has a local maximum. So if a convex shape has just one stable and one unstable equilibrium point, then the distance function has just one local minimum and one local maximum.

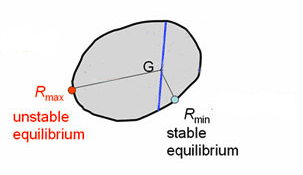
If the distance function has just one minimum and one maximum, then the shape can be cut into a small and a large part. This is a contradiction.

Now liberate the shape from its two glass plates, and allow it to swivel into the horizontal plane. The centre of gravity, call it G, is precisely the point on which you can balance the shape horizontally on the tip of a pencil. But it's impossible for G to be in the place we just described — closest to the stable equilibrium point and furthest from the unstable equilibrium point — if the distance function has just one local minimum and one local maximum. If it was in this position, then you could find a line passing through G which separates the shape into two pieces, with one piece much smaller in extent than the other. But now the shape could not possibly be balanced at G on the tip of a pencil, because it would topple off on the side of the larger piece. In fact, G in this case should not lie on the line, but within the larger of the two pieces of the shape. This is a contradiction, so our original assumption that the shape has just one stable and one unstable equilibrium point must have been false.

This argument can be made precise to give a rigorous mathematical proof — see the Gömböc website for more detail.