Stretch, but without the wrinkles

Submitted by mf344 on August 10, 2011

Back to the Constructing our lives package

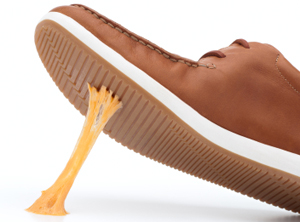
Like most materials, chewing gum contracts when stretched, causing it to wrinkle.

A team of nanoengineers have constructed new materials that don't wrinkle when you stretch them. This makes them similar to tissue found in the human body, so they may in the future be used to repair damaged heart walls, blood vessels and skin.

When you stretch a material, say a piece of fabric, it usually contracts in the directions transverse to the stretching, causing it to wrinkle up. This is called the Poisson effect and it’s measured by the Poisson ratio. Writing $strain_{axial}$ for the deformation of the material in the stretching direction and $strain_{trans}$ for the deformation in the transverse directions, the Poisson ratio is defined as

$\nu = -\frac{strain_{trans}}{strain_{axial}}.$

Deformations, or strains, are defined to be negative if they're compressive and positive if they're stretchy. This is the reason for the minus sign in the formula: it ensures that for a normal material, where stretching in one direction results in compression in the other directions, the Possion ratio is positive.

Materials that have a negative Poisson ratio — that expand in all directions when you stretch them — are very rare, but they do exist. They are called auxetic materials. Several types of human tissue, for example the interior surface of arteries, are auxetic. If we want to replace them with manufactured tissue, we need to emulate this exotic property.

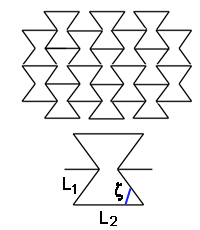
Figure 1: The reentrant honeycomb is made of bow tie shaped hexagons (top). The value of the Poisson ratio depends on the angle ζ and the lengths L₁ and L₂ of each hexagon (bottom).

This is what Shaochen Chen, now at University of California, San Diego, David Y. Fozdar, Pranav Soman, Jin Woo Lee and Li-Hsin Han managed to do during a research project at the University of Texas at Austin. Not only do the materials they constructed have negative Poisson ratios, it is also possible to make sure the ratios have exactly the right value to match that of natural tissues.

The secret of the two new materials lies in their geometry. Engineered tissue is made using a porous scaffold structure. It's the shape of the pores that's important. Square and circular pores, or those shaped like regular hexagons, give you a positive Poisson ratio. But it's possible to achieve a negative ratio by cleverly tweaking such basic geometries.

One of the new materials has the structure of a reentrant honeycomb, made up of hexagons that are shaped like bow ties (see figure 1). If you stretch this honeycomb so that the vertices nearest the centre of each bow tie get pulled apart, then the whole structure expands in all directions (see figure 2). Theory suggests that the corresponding Poisson ratio is

$\nu = \frac{ \sin {(90-\zeta )}(L_2/L_1+sin{(90-\zeta )})}{\cos ^2{(90-\zeta )}},$

where $L_1$ , $L_2$ and $\zeta$ are as in figure 1 (and the angle $\zeta$ is measured in degrees). This value is negative and it depends on the magnitude of the angle $\zeta$ and the ratio $L_2/L_1$ .

Figure 2: The reentrant honeycomb has a negative Poisson ratio. The image is from the team's paper, used here by permission.

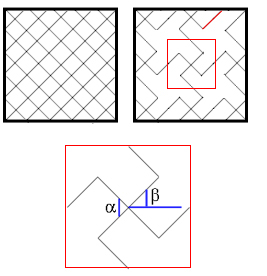Another auxetic structure comes from starting with a regular pattern made up of quadrilaterals and removing selected sides from it. The resulting missing rib structure, so theory predicts, also has a negative Poisson ratio. The formula that best matches experiments in this case is a little large to write down, but it shows that the Poisson ratio depends on the angles $\alpha$ and $\beta$ shown in figure 3.

Figure 3: The missing rib model is made by removing sides from a regular quadrilateral lattice (top). The Poisson ratio depends on the angles α and β (bottom).

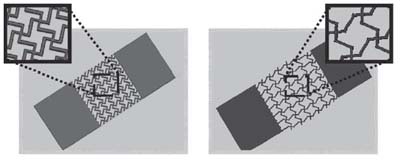Figure 4: The missing rib model also has a negative Poisson ratio. The image is from the team's paper, used here by permission.

It's been known for a while that the reentrant honeycomb and the missing rib meshwork have negative Poisson ratios, but this is the first time these structures have been constructed in a way that might be useful for medical applications. The team used a technique called digital micromirror device projecting printing (DMD-PP) to make their constructs. The material they used is called polyethylene glycol and is widely used in tissue engineering.

The team produced single and multi-layered versions of their new materials. The Poisson ratios they exhibited in experiments were in good agreement with those predicted by theory. And unlike other techniques for producing such structures, DMD-PP allows you to tightly control the geometry of the little pores. Since the theory predicts how this geometry impacts on the Poisson ratio, this makes it possible to create a material with exactly the right ratio to match natural tissue.

The team's next goal is to use their new materials in tissue grafts to repair damaged blood vessels. But they also hope that they will find applications further afield. "It's a new material. I think it's just a matter of time before more people will pick up and find applications for it in defense, energy and communications, for instance," says Chen. Their paper has been published in the journal Advanced functional materials.