
Swimming in mathematics
-->
As sporting glories continue in Beijing with the Paralympics taking up where the Olympics left off, many of us have marvelled at the architecture almost as much as at the sporting achievements. One of the Olympic venues, the National Aquatic Centre, lives up to its name of the Water Cube. It seems to be sliced from a giant foam of bubbles, an effect that is enhanced when it glows blue against the night sky.

The Water Cube at night. Image © Chris Bosse.
To achieve this appearance of foam, the engineers at ARUP and architects at PTW based their design on the work of two Irish physicists, Denis Weaire and Robert Phelan. In 1993 Weaire and Phelan found a new solution to the Kelvin problem: what is the most efficient way to divide a space into cells of equal volume, but with a minimal surface area?
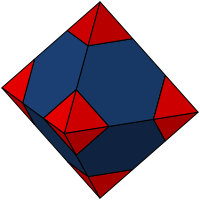
Kelvin's proposed solution was a structure made up of truncated octahedrons
This may sound complicated, but in fact every time you do the dishes the foam of soap bubbles you froth up demonstrates some of the properties of this structure. Soap bubbles and foams have the mathematical property of minimal surfaces — they take the structure which has the least amount of surface area to enclose a given volume. Lord Kelvin proposed a solution to the foam problem in 1887: he suggested that each cell was a truncated octahedron, a 14-sided solid formed by cutting the corners off a familiar three-dimensional diamond.
Kelvin did not provide any mathematical proof that his foam structure was in fact the one with the least surface area possible, but no better solutions were found for over a century until Weaire and Phelan's discovery. Their structure is made up of two types of irregular polyhedra — a wonky looking dodecahedron with pentagonal faces (that is, it has twelve faces each with five sides) and a wonky looking tetradecahedron with two hexagonal and twelve pentagonal faces (so it has fourteen faces, two with six sides, and twelve with five sides). In fact, just to make things more wonky, due to the laws of foams, both the Kelvin structure and the Weaire-Phelan structure have faces that are slightly curved.
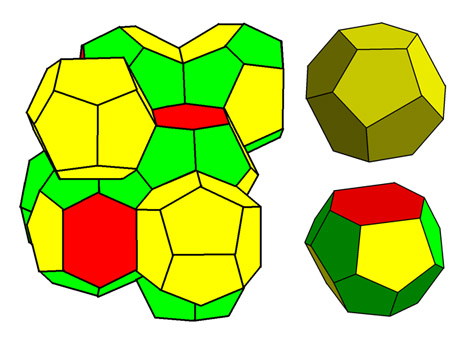
The Weaire-Phelan foam (left) is made up of wonky dodecahedrons with pentagonal faces (top right) and tetradecahedrons with 2 hexagonal and 12 pentagonal faces (bottom right).
"We soon found a curious feature about this foam. In spite of its complete regularity, when it is viewed at an arbitrary angle it appears totally random and organic, " said Arup Fellow Tristram Carfrae, when he explained why they based the Water Cube's design on the Weaire-Phelan structure. "We realised that a structure based on this unique geometry would be highly repetitive and buildable whilst appearing very organic and random. Indeed such space filling patterns are regularly observed in biological cells and mineral crystals, they are probably the most common structures in nature. Also the ductile space frame that is generated from this geometry is ideally suited to the seismic conditions found in Beijing."

Image © Arup Ben McMillan.
So we have the mathematics of Weaire and Phelan to thank for such an unusual and beautiful building, the structure of which appears to be made of the same water contained within. And although Weaire and Phelan showed that their foam has a smaller surface area (you can think of this as using less soap) than Kelvin's, they didn't manage to prove that it has the least surface area possible. So that's something else you can think about next time you are doing the dishes, or training for the 2012 Olympics.
Further reading
Plus has several articles on bubbles, minimal surfaces and architecture:
- Getting a handle on soap
- Double bubble is no trouble
- Still life
- Perfect buildings: the maths of modern architecture
- Career interview with Architect Wen Quek
This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
