
Text, Bytes and Videotape
Twenty Questions
Remember the game of "Twenty Questions"? One player thinks of a famous person, and the others have to work out who it is, by asking no more than 20 questions, the answer to which must be Yes or No.
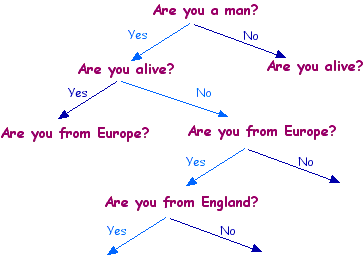
Twenty questions - Newton
You can think of the process as a "tree", where we set off from the first point and branch down. If Isaac Newton is the famous person - the sequence of answers would start "yes, no, yes, yes ..", or for simplicity "1011..".
There are 2 possible answers for each question, so there will be 220 = 1,048,576 possible sequences. Now, assuming there are less than a million famous people, the trick is to pick the right questions, so that there aren't two of them with the same sequence of 0s and 1s. How should we do this?
Well, here's a bad first question: "Are you Tony Blair?". OK, we might get lucky and win straight away, but nearly always the answer will be no, and we'll have wasted a question, because we'll know almost nothing more than when we started, having only got rid of one possibility.
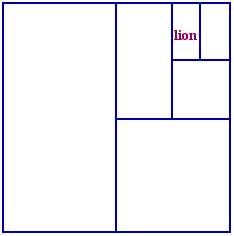
Catching a lion
A good first question is "Are you a man?". Whatever the answer is, we'll be able to cut the possibilities down by half. It's like trying to catch a lion by building fences halfway across a field - whichever side of the fence it is on, each time it gets half as much space.
Writing out the whole tree (on a big piece of paper!), we'd have a way of representing each of 1,048,576 people as a sequence of 0s and 1s. These 0s and 1s are called bits (see inset). We call this a coding of the people (when information theorists talk about coding, we don't mean secret codes like the German Enigma - that's a different area of maths, called cryptography).
Efficient codings
A coding is a rule linking one collection of objects (such as famous people, or letters of the alphabet) to another collection of things. Think of it as writing a label to put on each object (usually using only 0s and 1s). Perhaps the most famous coding is Morse Code, which converts letters of the alphabet into series of dots and dashes.
What we will be interested in is efficient coding - that is, a way of converting messages into short sequences of 0s and 1s. We suppose that the messages are created at random, and want to make the average number of bits needed as small as possible. The way we do this is to match very likely letters of the alphabet with short sequences of bits, and less likely letters with longer sequences. In Morse "E" is a single dot, whereas "Q" is dash-dash-dot-dash.
For example, in the game of Twenty Questions, each famous person isn't equally likely to be chosen, so we need to understand what to do if some possibilities are more likely than others. In fact we already know what to do. We stick to the principle that we should try and split things in half each time. The only change is that instead of trying to cut the number of people in half with each question, we try to cut the probability in half each time. This is what lies behind Huffman coding.
Huffman coding
At each stage, we bracket together the symbols with the lowest probabilities, and re-order the list. It's easiest to understand with an example.Suppose we have 5 letters: A appears with probability 1/2, and B,C,D,E appear with probability 1/8 each.
The simplest coding would be to pick 5 sequences of 3 bits each, and match them up with letters; say A = 000, B = 001, C = 010, D = 011, E = 100. Then the average letter would take 3 bits to describe. However, we can do much better than this, using the Huffman coding.
To create the Huffman coding:
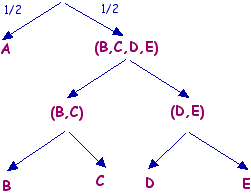
- At stage 1, bracket (D,E) together, then A has probability 1/2, (D,E) has probability 1/4, and B,C each have probability 1/8.
- At stage 2, bracket (B,C) together, then A has probability 1/2, (B,C) has probability 1/4 and (D,E) has probability 1/4.
- At stage 3, bracket ((D,E),(B,C) together, then A has probability 1/2 and so does (B,C,D,E).
Again, we can represent this in a tree, and again, we can read off the labels; A = 1, B = 011, C = 010, D = 001, E = 000. So, if we send a random letter, it will take on average \[(1/2) \times 1 + (1/8) \times 3 + (1/8) \times 3 + (1/8) \times 3 + (1/8) \times 3 = 2\] bits to describe.
Moving from 3 bits to 2 bits is what we call data compression. By exploiting our knowledge of the probabilities, we can save space. Even better, if we encode more than one letter, this method gives a decipherable message; for example, if someone stores the message 01101011000011, they can later break it apart (starting from the left) into 011/010/1/1/000/011 or BCAAEB.
It is a remarkable fact that this very simple Huffman coding offers the best possible performance. That is, there exists no coding from single letters A,B,C,D,E to collections of 0s and 1s which is (i) decipherable (ii) has a shorter average length with these probabilities. Try it and see! Furthermore this property has nothing to do with the particular probabilities. Whatever the collection of letters, and whatever their probabilities, the Huffman coding will always do best!
Entropy

Claude Shannon - father of information theory
There's a limit to how much you can compress a balloon full of air, because the molecules in the air can't be pushed into nothing. In the same way there is a universal limit to how much we can compress data. This amount of "stuff" in the file is called its entropy.
Shannon gave a general formula for the entropy. If the letters have probabilities $p(1), p(2), p(3), \ldots p(r)$, we will need at least $$ H = \sum_{s=1}^r \left( - p(s) \log_2 p(s) \right)$$ bits to express an average letter (the $\log_2$ means a logarithm to base 2). This suggests that if a letter has probability $p(s)$, we should try and encode it with a sequence of about $(-\log_2 p(s))$ bits. \par In the example above, $$ H = -1/2 \times (-1) - 1/8 \times (-3) - 1/8 \times (-3) - 1/8 \times (-3) - 1/8 \times (-3) = 2,$$ so the Huffman coding really is the best possible.
The entropy measures "how random something is". By calculating the entropy, we can see that the result of a fair 50%/50% coin toss (with entropy of 1) is "more random", and therefore harder to compress than a biased 90%/10% coin (with entropy of 0.46899).
Universal coding

That seems like the whole story. However, there is a big assumption we're making in describing Huffman coding, since we won't always know the probabilities. For example, consider trying to encode a book in a language like Russian where you don't know how likely each letter is to appear at each stage. Or consider the first photo of a strange planet - if we don't know what it looks like yet, we won't be able to work out probabilities of a particular colour appearing.
It turns out that a remarkable method invented by Lempel and Ziv in the 1970s avoids this problem altogether. It is called a universal data compression procedure, in that it works well even if we don't know the probabilities of particular letters. It works by spotting sequences of letters that have appeared before, and using the repeats to build up the message.
The rule is that we work through and break it up into "words". At each stage we want the shortest word we've not seen before.
If the letters are just A and B, and the message is:
ABAABABAABAAB
Put a slash in after the first letter, so the first word is A
A/BAABABAABAAB
Then the next symbol B isn't a word we've seen before, so put a slash after it too, so we've seen words A and B so far.
A/B/AABABAABAAB
Now, the symbol A is already on our list, so the next shortest possibility is AA, so put the slash in there. Continuing, we eventually obtain:
A/B/AA/BA/BAA/BAAB/
Now, to describe the message, each word will be very similar to one we've already seen. Thus, instead of saying "BAAB", we can write it as "BAA" (a word we've already seen) plus "B" (one extra letter). That is, "Word 5 + B".
I know this doesn't look very efficient, but it can be proved that even when we don't know the probabilities of As and Bs, this method becomes efficient for long enough messages, and comes close to the entropy.
Modern methods and the future

Data compression in action
Image from DHD photo gallery
There remain many unsolved problems in data compression. Ideas like Huffman and Lempel-Ziv coding are designed for the memoryless case. Dice rolls are memoryless - whatever has happened in the past doesn't affect the chances of the next roll coming up a 6. In the same way, Huffman coding works when letters are picked at random with the letters already picked not affecting what comes next.
However, if we want to compress music or videos, this won't be the case. For example, very often if a pixel is black, then the pixels next to it will be black (because it's part of a large black shape), and then in the next frame the pixel will also be black (because things don't change much from frame to frame). Many people are working on the most efficient way to compress video images, to take advantage of properties like this, so that videos can be sent quickly down a phone line.
There is also an issue of loss. The methods I've described produce a perfect copy of the data. However, if we are prepared to accept a small loss of quality, then often we can do better, as with MP3 files.
As this research continues, however, the principles and language devised by Shannon continue to form the basis of the work.
Bits and bytes
Bits are the simple building block of the modern information age, so it is worth getting used to thinking about them, just as we can estimate distances. Here is a quick explanation of bytes, megabytes, and so on, and some estimates of the storage requirements of various sorts of information.About the author

Oliver Johnson is a Fellow of Christ's College (old boys include Milton, Darwin, Richard Whiteley and Ali G).
He came to Cambridge as a student in 1992, and has found excuses not to leave ever since.
His research is in probability theory, trying to understand the structure behind randomness, using ideas related to this article.