Tsunami
Speed and power of a long tsunami wave, from Bernoulli's Theorem
Imagine that you're sitting in a low-flying jet just keeping pace with the tsunami in mid-ocean. You can see the ocean surface rushing past you at a speed of about 500 miles per hour. (We'll call the speed $U$.) You can't see the tsunami itself, however. Even a tsunami as energetic as the December 26th tsunami would be invisible. On its 2-hour journey westward toward Sri Lanka, for instance, that tsunami had a main crest whose height $h$ was not much more than a metre or so. The wavelength $L$ would have been roughly of the order of 200 miles, say 300km. So the maximum slope of the surface would have been roughly $2\pi h/L$ - only about 1 in 50,000. Such a tiny slope would be quite invisible from your vantage point. Indeed, the deep ocean is one of the safest places you can hang out when tsunamis are around, as long as you are well away from the site of the earthquake.
If you need an explanation of where the $2\pi$ came from, in the expression $2\pi h/L$ for the maximum slope, it will take a slight digression. If you'd prefer to skip it then skip the next paragraph.
Why $2\pi$?
The $2\pi$ is there because the surface has roughly the shape of a sine wave at a given instant, as suggested in the diagram below. In this side view, the wave height $h$ is greatly exaggerated to make the main crest and trough visible. The ocean depth $D$ is also exaggerated relative to the wavelength $L$. In a sine wave of length $L$ the surface elevation is $h\sin(2\pi x/L)$, where $x$ is distance along the wave. If you measure the wave height, the wavelength and the maximum slope in the diagram you will see that the slope is indeed $2\pi h/L$ to within measurement accuracy, roughly $6$ times $h/L$. Of course, if you know the rules of differential calculus, which is about finding the slopes of graphs, then you don't have to bother with measurement on a diagram. The rules tell you that the slope at any value of $x$ is $(2\pi h/L)\cos(2\pi x/L)$. Since the cosine has maximum value 1, the whole expression has maximum value $2\pi h/L$. This gives a reasonable idea of the order of magnitude, though in the real tsunami the wave shape is known to have been a bit more complicated with, in particular, a smaller crest and trough ahead of the main crest and trough. These provided some warning to people in Sri Lanka.
Back to Bernoulli
Now if you could see underneath the ocean surface, from your vantage point in the low-flying jet, you would see the water rushing past at all depths as suggested by the arrows in the diagram. The ocean floor is rushing past too.
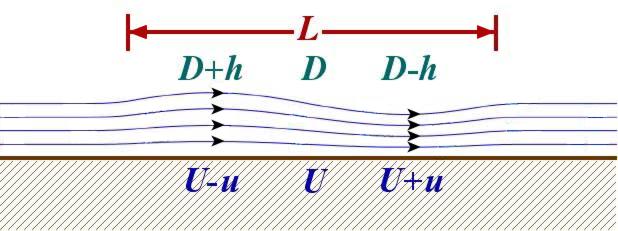
The tsunami on its way to Sri Lanka (vertical dimensions exaggerated).
Here is where we can use Bernoulli's theorem. We can use it because, from our viewpoint - just keeping pace with the tsunami - the flow is steady and the surface shape fixed. At the wavecrest, the ocean is a tiny bit deeper than average, with depth D + h. At the trough it is a tiny bit shallower, with depth D - h. We must also use the fact that the tsunami is hardly affected by viscosity - Bernoulli's theorem assumes that viscosity is negligible.
When all these conditions are met, the theorem relates half the square of the flow speed to the pressure and the elevation of a streamline. Details and further discussion are given about midway through the article Understanding turbulence from Issue 1 of Plus.
So, to use Bernoulli's theorem we have to say something about the flow speed. From our viewpoint, the flow past the crest has to be a little slower than U, with speed U - u say. The flow past the trough has to be a little faster, with speed U + u. If we assume that u is independent of depth - which is approximately correct for long waves, though not for pond waves - then
$$ (D + h)(U - u) \;=\; (D - h)(U + u). $$In other words, in this steady flow the amount of water rushing past the crest, per unit time, is the same as the amount of water rushing past the trough.
You can rewrite the equation as
$$ DU + hU - Du - hu \;=\; DU - hU + Du - hu. $$Notice the pattern of signs. We can subtract DU - hu from both sides, leaving
$$ hU - Du \;=\; -\,hU + Du, $$which implies that
$$ hU \;=\; Du. $$Now Bernoulli's theorem takes an especially simple form at the surface, because we can neglect pressure differences. (That's because air is so much less massive than water. The density of air is about a thousandth of the density of water.) The tsunami therefore behaves very nearly as if the pressure were constant at the surface. So the pressure terms cancel and the theorem tells us simply that
$$ \frac{1}{2} (U - u)^2 + gh \;=\; \frac{1}{2} (U + u)^2 - gh. $$This relation says that a piece of water at the surface behaves just like a frictionless ice-hockey puck whizzing along over a gently undulating ice surface. It's almost the same behaviour as that of a frictionless bicycle coasting along a gently undulating road. That should be no surprise since we said that viscosity - i.e. fluid friction - can be neglected. The puck or bicycle goes slowest on a crest and fastest in a trough, by the small amount u, and so does the water at the surface. In this situation, with no significant pressure force, Bernoulli's theorem is the same thing as the energy-conservation theorem for a frictionless particle under gravity g. Kinetic energy plus gravitational potential energy is constant.
Notice that we can rewrite the last equation as
$$ \frac{1}{2} (U^2 - 2Uu + u^2) + gh \;=\; \frac{1}{2} (U^2 + 2Uu + u^2) - gh. $$So by subtracting $\frac{1}{2} U^2 + \frac{1}{2} u^2$ from each side and rearranging the result, we see that $$ gh = Uu. $$ But we have already seen, from the constancy of volume flow, that $hU = Du$. Therefore $$ hU = Du = D(Uu)/U = D(gh)/U. $$ So $hU = Dgh/U$; and the factors $h$ cancel to give $U = gD/U$. Multiplying by $U$ we see that $U^2 = gD$ and hence that $$ U = \surd(gD), $$
as claimed earlier.
The power of the tsunami
What was the power of the tsunami arriving onshore at Sri Lanka? Here we can give the word "power" a precise technical meaning. Power means the rate of transfer of energy. In standard scientific units, i.e. using the SI or the MKS (metre-kilogram-second) system, power is measured in watts. It is the same unit as for electrical power, of course. The only difference is that the energy being transferred is mechanical rather than electrical. For the tsunami we may calculate the power per metre of shoreline. So the units will be watts per metre. We'll see in a moment that the answer is of the order of a megawatt per metre. This is equivalent to a gigawatt - a thousand million watts - for each kilometre of shoreline. The total power hitting Sri Lanka was nearly half a terawatt, half a million million watts. You might like to compare this with the world's total electrical power-generation capacity, which is a few terawatts.
Here's the simplest way to calculate the power. (I'm going to gloss over some wave-mathematical technicalities, but they make no difference to the final answer.) In mid-ocean, our long waves have kinetic energy $\frac{1}{2} u^2$ per unit mass. The mass of a column of water a square metre in cross-section and $D$ metres tall is $\rho D$, where $\rho$ is the density of water, about one tonne per cubic metre. So, per unit horizontal area, we are talking about an energy $\frac{1}{2}\rho D u^2$. So as the waves approach the shoreline the power $P$, calculated as the rate at which kinetic energy is transferred shorewards, is the energy times the wave speed $U$,
$$ P \;=\; \frac{1}{2}\rho DU u^2 \;=\; \frac{1}{2}\rho D\surd(gD) u^2. $$When $h$ has the value 1 metre in the open ocean, with $U$ around 220 metres per second, we see from the relation $hU = Du$ derived earlier that $u = hU/D = h\surd(gD)/D = h\surd(g/D) = 0.045$ metres per second. It doesn't sound much, but remember the large wave speed $U$ and the huge mass of water; $\rho D$ is $1000 \times 5000 = 5,000,000$ kilograms per square metre of ocean surface. So in MKS units $P=\frac{1}{2}\times1000\times5000\times\surd(10\times5000)\times0.045^2 = 1.1\times 10^6$ watt per metre of shoreline - just over a megawatt. As already said, this means a gigawatt per kilometre of shoreline. That's more than enough to do a lot of damage.
At Phuket, Thailand, there is an extensive shallow region with a large coral reef offshore. So a fairly large proportion of the energy was dissipated by wave breaking, before the rest of it crashed into the inhabited areas. Without that shallow region and coral reef, things would have been much worse.
About this article
Michael McIntyre is a Fellow of the Royal Society and a professor of applied mathematics at the Centre for Mathematical Sciences in the University of Cambridge. This Plus article is appearing concurrently with a shorter version commissioned by the Independent Newspaper's new sixth-form careers magazine TheGuide: MATHEMATICS. We are grateful to Professor James Jackson FRS for supplying several of the images and for advice on plate tectonics.
For further information, a reliable source is the website of the Tsunami Research Program of the Pacific Marine Environmental Laboratory in Seattle, Washington, USA.