icon

Having fun with unit fractions

Yutaka Nishiyama Share this page
Submitted by Marianne on 9 February, 2012

The number 1 can be written as a sum of unit fractions, that is, fractions which have 1 in the numerator. For example,

  \[ 1=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}. \]    

Multiplying both sides by 6 we get

  \[ 6=3+2+1, \]    

which shows that the equation holds.

Ruler

How long can we make such a sum without repeating any of the unit fractions in it? It's a question I began thinking about around 20 years ago when I started work on a problem involving unit fractions. I decided to restrict myself to unit fractions with two-digit denominators, in other words, natural numbers no greater than 99.

By trial and error I managed to find a sum of 42 terms that met the conditions. I also learned that different methods of decomposition lead to different solutions. What I did not accomplish was a proof that 42 was the largest possible number of terms, so for all I know a 43-term solution awaits.

In this article I would like to show how I found my 42-term solution. This is a fun problem to work on, so the motivated reader may wish to take a stab at it before reading on and then compare our solutions.

Starting with perfect numbers

A natural number $m$ is called a perfect number if the sum of its divisors (including 1, but excluding $m$) equals itself. As an example, 6 is a perfect number (as you can see above), as is 28 (with divisors 14, 7, 4, 2, and 1):

  \[ 28=14+7+4+2+1. \]    

Dividing both sides by 28 results in a decomposition of 1 into a sum of unit fractions with five terms:

  \[ 1=\frac{1}{2}+\frac{1}{4}+\frac{1}{7}+\frac{1}{14}+\frac{1}{28}. \]    

There are many other perfect numbers (496, 8128, 33550336, and 8589869056, for example). While we could similarly decompose these numbers as above, the condition that each denominator must be 99 or less limits which ones we can use. For example 496 is out because two of its divisors have three digits:

  \[ 496=248+124+62+31+16+8+4+2+1. \]    

So let’s leave perfect numbers to one side and take another approach. Since we know that we will be dealing with unit fractions, we can save space by omitting the unit numerators, writing fractions like $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{6}$ as $/2$, $/3$, $/6.$

Clearly we can make sums of unit fractions adding up to 1 longer by decomposing each individual unit fraction into a sum of unit fractions. For example,

  \[ /3 = /4+/12 \]    
  \[ /6=/7+/42. \]    

We can generalise our methods for decomposition and composition into five rules.

Rule 1: Decomposition into two terms

Let’s look at how a unit fraction $/n$ can be decomposed into two different unit fractions. Assume that the unit fraction’s denominator can be factored as $n=a\times b$ , where $a$ and $b$ are allowed to be 1. This allows for decomposition into two unit fractions, as follows:

  \[ /n=/(a \times b) = (a+b)/((a \times b)\times (a+b)) = /(b \times (a+b))+/(a \times (a+b)). \]    

For example, for the unit fraction $/30$ we have $n=30$ which can be factored as $30=5 \times 6$. Then,

  \[ a+b=5+6=11, \]    
  \[ a \times (a+b)=55, b \times (a+b)=66, \]    
  \[ /30=/55+/66. \]    

We can repeat this to create as many decompositions as we like. Doing so to $/3$ and $/6$ results in

  \[ /3=/(1\times 3) = /(1\times (1+3))+/(3 \times (1+3))=/4+/12. \]    

and

  \[ /6=/(1\times 6)=/(1 \times (1+6))+/(6 \times (1+6))=/7+/42. \]    

Doing this is relatively simple by hand, but you can also use spreadsheet software to speed things along.

Rule 2: Decomposition into n terms

Multiplying the denominator $a$ of $/a$ by $n$ decomposes the unit fraction into $n$ unit fraction terms with $n\times a$ as a denominator:

  \[ /a=/(n \times a)+/(n \times a)+ ... /(n \times a). \]    

Using cases of $n=2$ or $n=3$ we get

  \[ /4=/8+/8 \]    

and

  \[ /8=/24+/24+/24. \]    

Rule 3: Decomposition into two terms by another method

After performing the standard decomposition of $\a $ into two terms the denominator of each unit fraction can by multiplied by $n$ to create a decomposition of $/(n \times a).$

  $\displaystyle \nonumber /a $ $\displaystyle = $ $\displaystyle /b+/c $    
  $\displaystyle \nonumber /(n \times a) $ $\displaystyle = $ $\displaystyle /(n \times b) + /(n \times c). $    

For example,

  $\displaystyle \nonumber /4 $ $\displaystyle = $ $\displaystyle /5+/20 $    
  $\displaystyle \nonumber /(2 \times 4) $ $\displaystyle = $ $\displaystyle /(2 \times 5)+/(2 \times 20) $    
  $\displaystyle \nonumber /8 $ $\displaystyle = $ $\displaystyle /10+/40. $    

Rule 4: Decomposition into three terms

Let us now consider how we might decompose a unit fraction $/m$ into three terms. The key to doing so is finding three numbers $a,$ $b,$ $c$ such that their least common multiple is the denominator $m.$ We then multiply the numerator and the denominator of the original unit fraction $/m$ by the sum of those three numbers, $a+b+c$.

  $\displaystyle \nonumber /m $ $\displaystyle = $ $\displaystyle (a+b+c)/(m \times (a+b+c)) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle a/(m \times (a+b+c)) + b/(m \times (a+b+c))+c/(m \times (a+b+c)). $    

Since the least common multiple of $a,$ $b,$ and $c$ is $m,$ we know that each of $a,$ $b,$ $c$ will divide $m$. In other words, $a/m,$ $b/m,$ and $c/m$ are each unit fractions. When the denominators are multiplied by $(a+b+c)$ we will again have unit fractions.

Let’s take $/12$ as an example. Three numbers having 12 as their lowest common multiple are 3, 4, and 6, the sum of which is $3+4+6=13.$ We therefore want to multiply the denominator of the unit fraction $/12$ by $(3+4+6).$

  $\displaystyle \nonumber /12 $ $\displaystyle = $ $\displaystyle (3+4+6)/(12\times (3+4+6)) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 3/(12\times 13)+4/(12 \times 13) + 6/(12 \times 13) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 1/(4 \times 13)+1/(3 \times 13) + 1/(2 \times 13) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 1/52 + 1/39 + 1/26. $    

Another three numbers having 12 as their lowest common multiple are 2, 4, and 6. The sum in this case is $2+4+6=12,$ so we proceed in the same manner.

  $\displaystyle \nonumber /12 $ $\displaystyle = $ $\displaystyle (2+4+6)/(12\times (2+4+6)) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 2/(12\times 12)+4/(12 \times 12) + 6/(12 \times 12) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 1/(6 \times 12)+1/(3 \times 12) + 1/(2 \times 12) $    
  $\displaystyle \nonumber $ $\displaystyle = $ $\displaystyle 1/72 + 1/36 + 1/24. $    

Rule 5: Composition of two terms into one

Occasionally in the process of constructing a sum of unit fractions it might be useful to replace two existing unit fractions by one which then gives us more possibilities. For example, given the decomposition into two terms
  \[ /15 = /18 + / 90, \]    
we can swap the left and right sides to create a composition of two terms.
  \[ /18 + / 90 = /15. \]    

Using these five rules I have found a decomposition of 1 into 42 distinct unit fraction terms. You can see it below.

Repeated decomposition and composition of two and three terms to find increasingly long sums equal to 1 is an excellent way to kill time. But just how far can we take it? A bit of integral calculus allows one to predict that the maximum value must be 62. (If you're not familiar with calculus, you can skip this section.)

A maximum of 62 terms

We will compare the sum of the unit fractions with an integral of the function $f(x)=1/x.$

Figure 1 shows the function between $x=1$ and $x=n$ (where we take $n$ to be a natural number greater than 1). Clearly, the sum of the areas of the rectangles shown in the figure is larger than the area under the curve between these two points.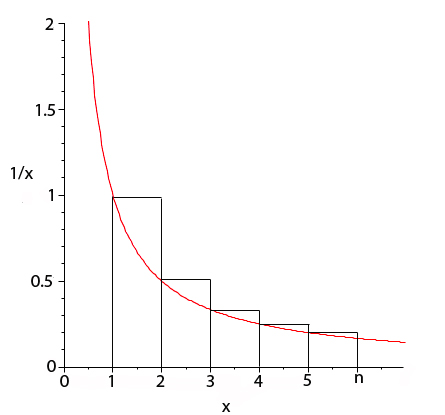

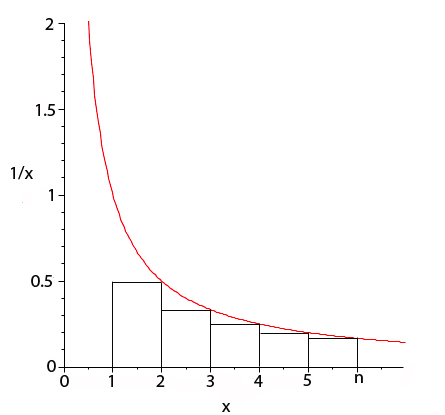
Graph

Figure 1

The horizontal side of each rectangle has length 1. The vertical side of the first rectangle has length $f(1)=1.$ The vertical side of the second rectangle has length $f(2)=1/2.$ The vertical side of the third rectangle has length $f(3)=1/3.$ Continuing this we see that the vertical side of the $ith$ rectangle has length $f(i)=1/i.$ Altogether there are $n-1$ rectangles.

Thus, the sum of the areas of the rectangles is

  \[ 1+\frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n-1}. \]    

Comparing this to the area under the curve between $x=1$ and $x=n$, which is the integral of $f(x)$ between $x=1$ and $x=n$, we have

  \[ \int _1^ n \frac{1}{x}dx < 1+\frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n-1}. \]    

Figure 2 shows the same curve, this time with rectangles whose areas sum to less than the area under the curve.

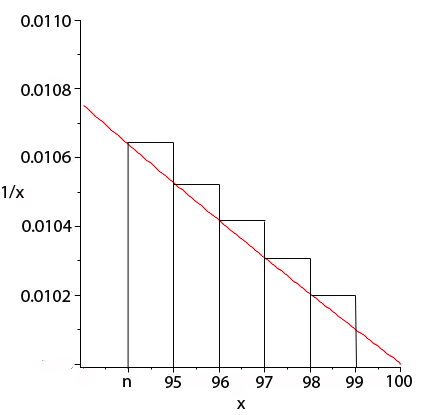
Graph

Figure 2

Here the vertical side of the $ith$ rectangle has length $1/(i+1)$ so the sum of the areas is

  \[ \frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n}. \]    

This gives

  \[ \frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n} <\int _1^ n \frac{1}{x}dx. \]    

Putting the two inequalities together we have

  \begin{equation} \frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n} <\int _1^ n \frac{1}{x}dx < 1+\frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n-1}.\end{equation}   (1)

Now note that

  \[ 1 + \left(\frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n}\right) = 1+\frac{1}{2}+ ... +\frac{1}{n} < \int _1^ n \frac{1}{x}dx + 1 \]    

and

  \[ \int _1^ n \frac{1}{x}dx + \frac{1}{n} < \left(1+\frac{1}{2}+\frac{1}{3}+ ... +\frac{1}{n-1}\right) + \frac{1}{n}, \]    

giving

  \begin{equation} \int _1^ n \frac{1}{x}dx + \frac{1}{n} < 1+\frac{1}{2}+...+\frac{1}{n}< \int _1^ n \frac{1}{x}dx + 1.\end{equation}   (2)

Since the integral of $f(x)=1/x$ is $\log {x}$ we get

  \[ \log {n} +\frac{1}{n} < 1+\frac{1}{2}+...+\frac{1}{n} < \log {n}+1. \]    

Now if we want to create a sum of unit fractions that’s as long as possible but does not exceed 1, it is best to use fractions with large denominators: the larger the denominators, the smaller the fractions themselves and the more terms we can add before we reach 1. So instead of looking at sums from 1 to $\frac{1}{n}$, let’s looks at sums from $\frac{1}{n}$ to $\frac{1}{99}:$

  \[ \frac{1}{n}+\frac{1}{n+1}+...+\frac{1}{99}. \]    

We then see how small we can make $n$ before the sum becomes larger than 1.

The argument we used to construct our inequalities above would have worked just as well if we had taken $x=n$ and $x=99$ as the limits of integration instead of $x=1$ and $x=n$. It’s just a matter of shifting the picture along the $x$-axis.

Graph

Figure 3

In analogy to inequality (1) this gives

  \[ \frac{1}{n+1}+...+\frac{1}{99}<\int _ n^{99} \frac{1}{x}dx < \frac{1}{n}+\frac{1}{n+1}+...+\frac{1}{98}. \]    

A similar manipulation as above then gives the analogue of inequality (2)

  \[ \int _ n^{99} \frac{1}{x}dx + \frac{1}{99} < \frac{1}{n}+\frac{1}{n+1}+...+\frac{1}{99} < \int _ n^{99} \frac{1}{x}dx +\frac{1}{n}. \]    

Working out the integral gives

  \[ \log {99} - \log {n} +\frac{1}{99} < \frac{1}{n}+\frac{1}{n+1}+...+\frac{1}{99} < \log {99} - \log {n}+\frac{1}{n}. \]    

The inequality on the right says that in order for the sum of the unit fractions to not exceed 1 we must have

  \[ \log {99} - \log {n} + \frac{1}{n}\leq 1. \]    

Solving for $n$ we get

  \[ n \geq 38. \]    

This gives the sum

  \[ S_1=\frac{1}{38}+\frac{1}{39}+ ... +\frac{1}{98}+\frac{1}{99} \approx 0.976, \]    

which has $99-38+1=62$ terms.

Now any sum involving 63 terms or more will be at least as large as

  \[ S_2= \frac{1}{37}+S_1 \]    

because $S_2$ involves all the smallest unit fractions with two-digit denominators. And since $S_2>1$, as we’ve just seen, this means that any 63-term sum is greater than 1. In particular, any sum that adds up exactly to 1 can have at most 62 terms. I have found a 42-term decomposition, so a maximum of 62 sounds reasonable.

A tree diagram of my 42 term solution

My current solution with 42 distinct unit fraction terms looks like this

  $\displaystyle \nonumber 1 $ $\displaystyle = $ $\displaystyle /15 + /17+ /20 + /21 + /22+ /26 + /27 + /30 + /32 + /33 $    
  $\displaystyle \nonumber $ $\displaystyle + $ $\displaystyle /34 + /35 + /36 + /38 + /39 +/40 + /42+ /44 + /45 + /48 $    
  $\displaystyle \nonumber $ $\displaystyle + $ $\displaystyle /50 + /52+ /54 + /55 + /56 + /60 + /63 + /66 + /70 + /75 $    
  $\displaystyle \nonumber $ $\displaystyle + $ $\displaystyle /76+ /77+ /78 + /80 + /84 + /85 + /88 + /90 + /91 + /95 $    
  $\displaystyle \nonumber $ $\displaystyle + $ $\displaystyle /96 + /99. $    

The replacement

  \[ /15 + /30 + /90 = /18 + /24 + /72 \]    

will give you an alternative 42-term answer, which I leave for you to work out (here is the answer).

Figure 4 shows the solution as a tree diagram, in which the trunk is our original value of 1 and the branches show the process of decomposition into two and three terms. Each of the 42 leaves is a unique unit fraction term in the solution.

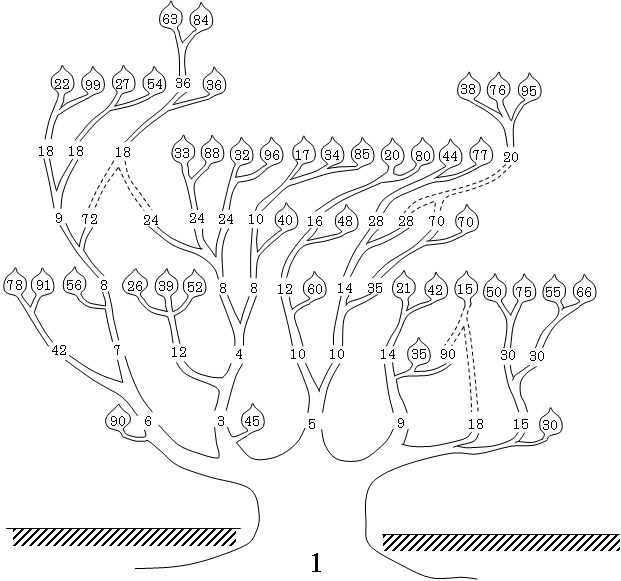
Tree diagram

Figure 4

I enjoy graphs like this, but a botanist might be disturbed by the floating branches (connected by dotted lines). These result from the compositions, that is replacing two unit fractions by one according to rule 5, I performed in the process:

  \[ /90 + /18 = /15 \]    
  \[ /72 + /24 = /18 \]    
  \[ /28 + /70 = /20. \]    

Perhaps a bit more searching would repair those places by removing the need for the compositions.

About the author

Yutaka Nishiyama is a professor at the Osaka University of Economics, Japan, where he teaches mathematics and information. He is proud to be known as the "boomerang professor". He is interested in the mathematics of daily life and has written eight books about the subject. The most recent one, The mystery of five in nature, investigates, amongst other things, why many flowers have five petals.

Read more about...
number theory
arithmetic
unit fraction

Comments

Permalink Submitted by petermabey on 28 February, 2012

A related problem is that of representing integers greater than 1 by unit fractions: it is clear that as the harmonic sum is divergent, such should be always possible. Adding terms till the next one would pass the target, and then proceeding by using the greedy algorithm should give a very inefficient solution, but a better one will have fewer terms.
The best solution could be defined either as the one with the fewest terms, or that with the largest final denominator - I don't know if these are necessarily the same.
Is there any information on how the number of terms is related to the target ?

Permalink Submitted by Anonymous (not verified) on 8 March, 2012

1/2 + 1/(2*3) + 1/(3*4) + 1/(4*5) + 1/(5*6) + ...
= (2-1)/2 + (3-2)/(2*3) + (4-3)/(3*4) + (5-4)/(4*5) + (6-5)/(5*6) + ...
= (1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + (1/4 - 1/5) + (1/5 - 1/6) + ...
= 1 + (-1/2 + 1/2) + (-1/3 + 1/3) + (-1/4 + 1/4) + (-1/5 + 1/5) + (-1/6 + ...
= 1 + 0 + 0 + 0 + ) + ...
= 1

Kermit Rose
kermit@polaris.net

Permalink Submitted by Anonymous (not verified) on 16 June, 2014

I read this article and decided to try composing and decomposing unit fractions for myself. Several notepads some coffee and a ballpoint pen later I have created a neat method of splitting 1 into a maximum number of different unit fractions below one hundredth.
My method stretches the rules above, by using numerators and denominators higher than 1/99 during construction. But it is simple, elegant and can be quickly calculated on a sheet of paper. I am confident that I could produce a proof of the maximum number of unit fractions (below one hundredth) that decompose 1. Is this something new or am I rediscovering the wheel, or just missing something? I would love to share my idea with somebody in the know. Thanks again for the inspiring article!

  • Maths in a minute

    Want facts and want them fast? Our Maths in a minute series explores key mathematical concepts in just a few words.